Project: Approximate the Profile of a Bird

8. Project: Approximate the Profile of a Bird#

8.1. Introduction#

In this project, you will write a MATLAB code to get a curve to approximate the top profile of a bird. To get started with this project, you will need to download the starter code and unzip its contents to the directory where you wish to complete the project.

Files included in this project

  • * project8.m - MATLAB script that steps you through the project.

  • divdif.m - Divided difference of the function.

  • interp.m - Newton divided difference form of the interpolation polynomial.

You need to complete the files with *.

Throughout the project, you will be using the script project8.m. This script set up all dataset for the problem and make calls to functions that you will write. Do not modify it. You are only required to modify functions in * files, following the instructions in this project.

8.2. Assignments#

Part 1 - Plot Data#

The first part of project8.m gives you practice with plotting data in MATLAB.

An array named data is given in this code. It has 2 column and 21 rows. Every row is a point. The first column is x coordinate and the second column is y coordinate. So we need to extract x and y from data. Then we use plot function to plot the data as scatter.

Now type the following code in Part 1:

x = data(:,1);
y = data(:,2);
h1 = plot(x,y,'o','linewidth',3);

data(:,1) means the first column of the array data and we set this vector as x; data(:,2) means the second column of the array data and we set this vector as y. Then we use h1 = plot(x,y,’o’,’linewidth’,3) to plot these points. For more details of function plot, you can type help plot in MATLAB command line.

Now you can run project8.m. At first, it will show you picture of bird, as following:

_images/16.png

Then you need press Enter key to continue and it will show you the data points indicated by some blue circles on the bird:

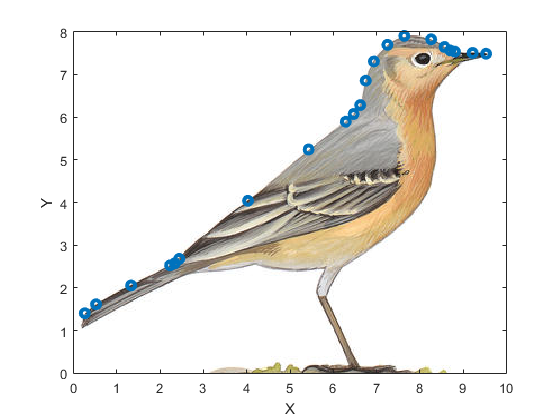
_images/24.png

We will use these points to approximate the top profile of the bird.

Now project8.m will pause until you press any key, and then will run the code for the next part of the project. If you wish to quit, typing ctrl-c will stop the program in the middle of its run.

Part 2 - Use polynomial to approximate profile#

In last project, you have written the code of Newton’s divided difference interpolation. In this part, we will use this code to plot a polynomial to approximate the profile of the bird and see what will happen. The code files of Newton’s divided difference interpolation are given, named divdif.m and interp.m. You don’t need to modify them.

Now go to the second part of project8.m, you will find a variable x_eval is given. It contains the x values of the points we will approximate. Our goal is to approximate the y values of these points by Newton’s divided difference interpolation.

Now type the following code in Part 2:

D = divdif(x,y);
y_eval = interp(x,D,x_eval);
h2 = plot(x_eval,y_eval,'-','linewidth',3);

The first line gives the divided differences and the second line use these divided differences to interpolate the y value of x_eval. The third line plots these new points by a solid line. Now you can run project8.m and you will see the following figure:

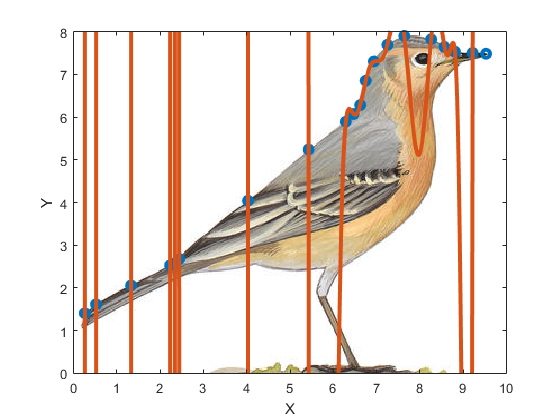
_images/32.png

The interpolating polynomial in this case is of degree 20 and oscillates wildly. It produces a very strange illustration of the top of the bird.

Part 3 - Use spline to approximate profile#

In this part, we will use MATLAB build-in function spline to approximate the top file of the bird. Now type the following code in Part 3 of project8.m:

y_eval=spline(x,y,x_eval);
h3 = plot(x_eval,y_eval,'-','linewidth',3);
set(h2,'visible','off')

The first line use the data points to obtain the y value of x_eval by cubic spline. The second line will plot the new points (x_eval, y_eval) by a solid line. The third line will make the polynomial we get in Part 2 invisible, to make the graph more clear. Now you can run project8.m and you will see the following figure:

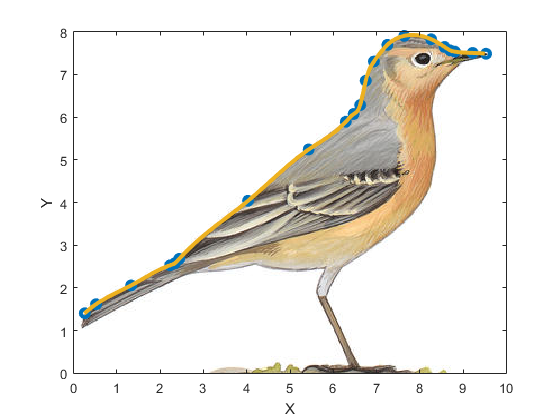
_images/44.png

From this figure, we find the cubic spline curve is nearly identical to the top profile of the bird.

8.3. Submit your code#

This is the last step. You should submit your code files to WTClass. After clicking Browse My Computer, you should select all files listed in Introduction to upload. Failure to do so will affect your grade.

Contents