Project: Bisection Method

3. Project: Bisection Method#

3.1. Introduction#

In this project, you will use bisection method to find roots of linear equations. To get started with this project, you will need to download the starter code and unzip its contents to the directory where you wish to complete the project.

Files included in this project

  • project3.m - MATLAB script that steps you through the project.

  • checkMyAnswer.m - MATLAB script that checks your code.

  • checkMyAnswer.mat - Data set.

  • data.mat - Data set.

  • * f.m - Function \(f(x)\) to find the root.

  • * bisection.m - Bisection method.

You need to complete the files with *.

Throughout the project, you will be using the script project3.m. This script set up all dataset for the problem and make calls to functions that you will write. Do not modify it. You are only required to modify functions in * files, following the instructions in this project.

3.2. Assignments#

Part 1 - Define the function f#

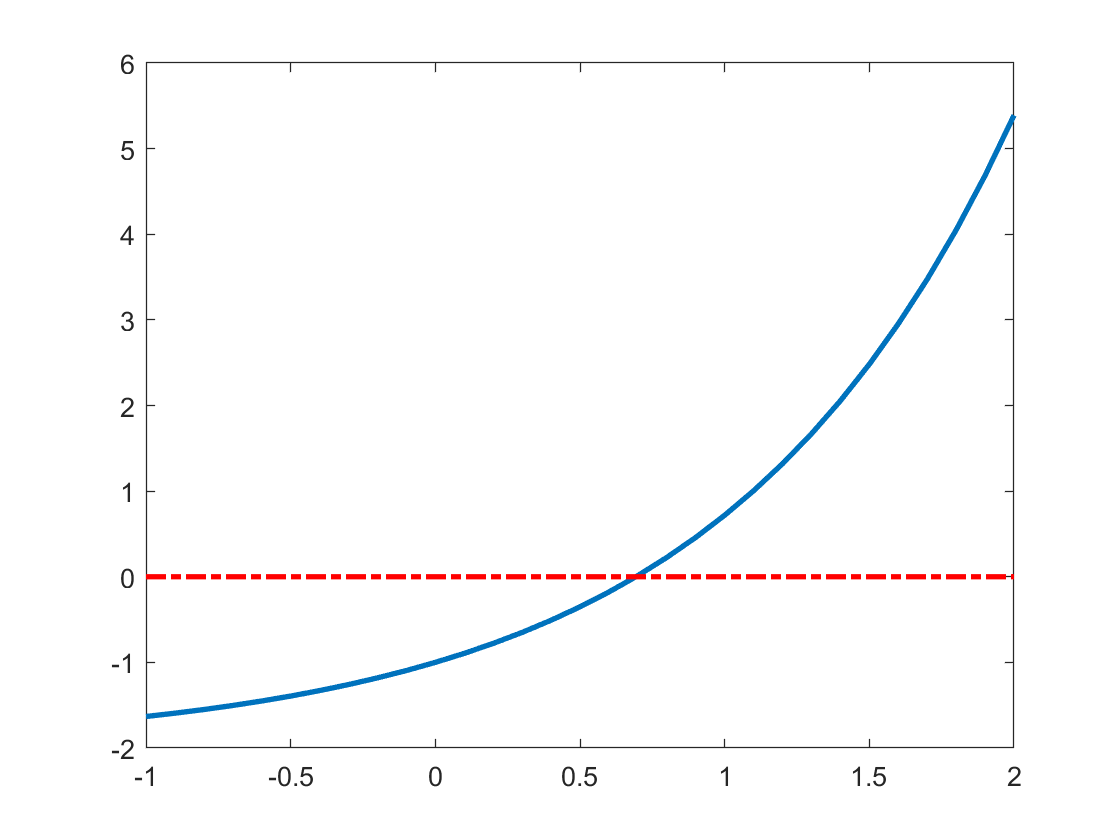
In this part, you need to modify the file f.m to return the function \(f(x)=e^x-2\). Once complete, run project3.m and it will show you the graph of function \(f(x)=e^x-2\) as follows:

_images/0.png

Part 2 - Bisection Method#

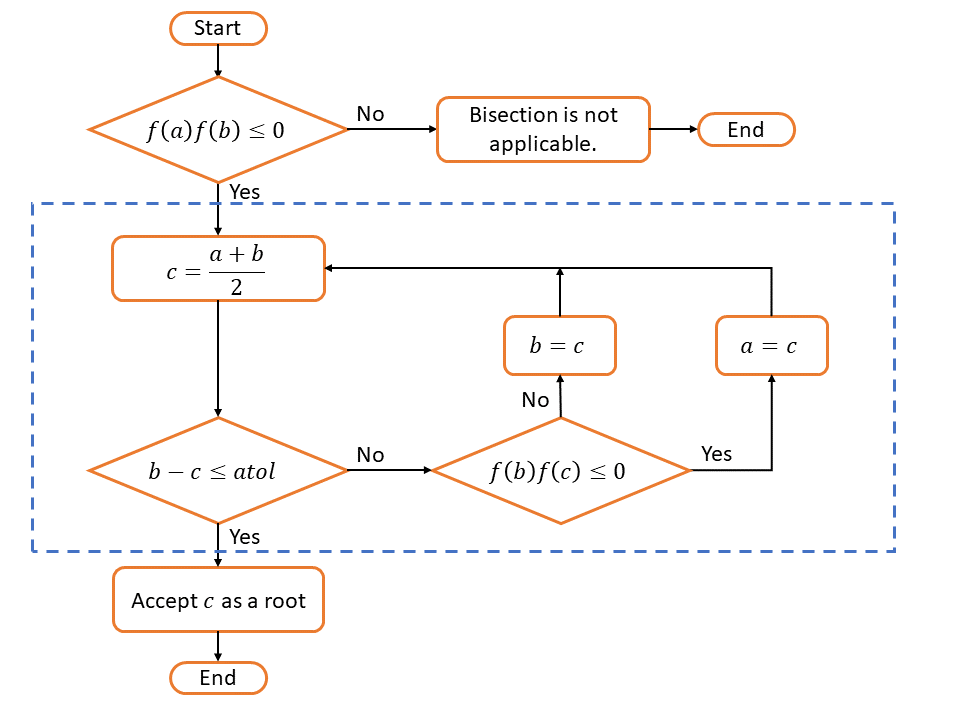
In this part, you will practice bisection method in MATLAB to find the approximation of \(\ln 2\) accurate to within \(atol=10^{-8}\). It is easy to find \(\ln 2\) is the root of function \(f(x)=e^x-2\). By the graph in last part, we can find a good initial interval where \(a=0.5\) and \(b=1.0\). You need to modify bisection.m to return the root of the function of \(f(x)=e^x-2\) by bisection method. Recall the bisection method consists of the following steps:

Algorithm 3.1 (Bisection Method)

  1. Define \(c=(a+b)/2\).

  2. If \(b-c\le atol\), then accept \(c\) as the root and stop.

  3. If \(f(b)\cdot f(c)\le 0\), then set \(a=c\). Otherwise, set \(b=c\). Return to step 1.

The following flowchart can help you understanding the process.

_images/12.png

Hint

  • Use a for loop or while loop to implement the cycle in the blue rectangle.

  • If you use for loop, after accepting c as root, do not forget use a break keyword to escape the loop.

Once complete, run project3.m. You should see output:

The approximation of ln(2) by Bisection Method is 0.693147175

3.3. Submit your code#

This is the last step. You should submit your code files to WTClass. After clicking Browse My Computer, you should select all files listed in Introduction to upload. Failure to do so will affect your grade.

Contents