Project: Gaussian Elimination

5. Project: Gaussian Elimination#

5.1. Introduction#

In this project, you will practice how to use Gaussian Elimination (with partial pivoting) to solve linear systems in MATLAB. To get started with this project, you will need to download the starter code and unzip its contents to the directory where you wish to complete the project.

Files included in this project

  • project5.m - MATLAB script that steps you through the project.

  • checkMyAnswer.m - MATLAB script that checks your code.

  • checkMyAnswer.mat - Data set.

  • data.mat - Data set.

  • * GE.m - Gaussian Elimination without pivoting.

  • * GEpivot.m - Gaussian Elimination with pivoting.

You need to complete the files with *.

Throughout the project, you will be using the script project5.m. This script set up all dataset for the problem and make calls to functions that you will write. Do not modify it. You are only required to modify functions in * files, following the instructions in this project.

5.2. Assignments#

Part 1 - Gaussian Elimination#

Recall the algorithms of Gaussian Elimination and Backward substitution:

Algorithm 5.1 (Gaussian Elimination and Backward Substitution)

Given a real, nonsingular \(n\times n\) matrix \(A\) and a vector \(\mathbf{b}\) of size \(n\), first transform into upper triangular form,

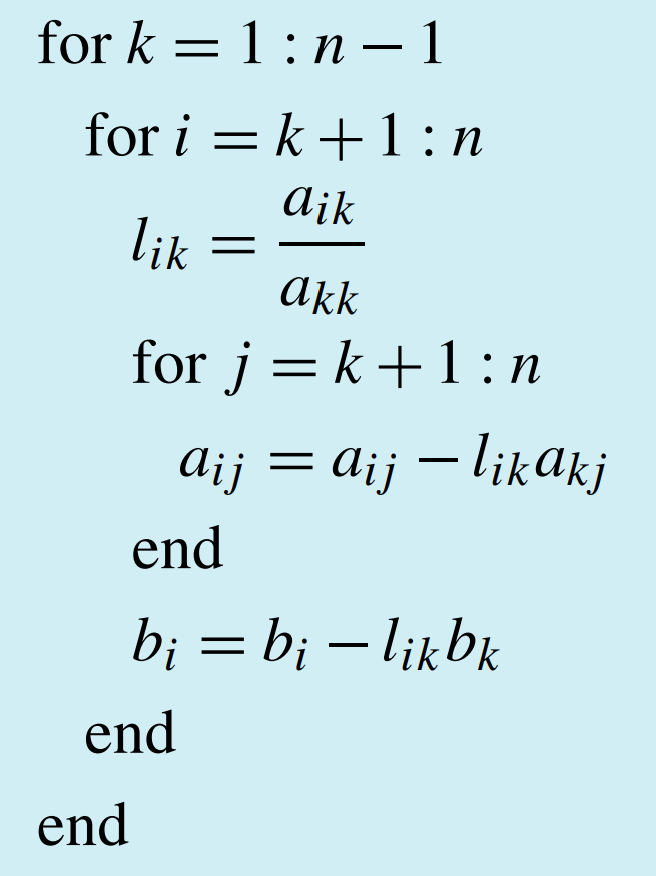
_images/14.png

Then apply the algorithm of backward substitution.

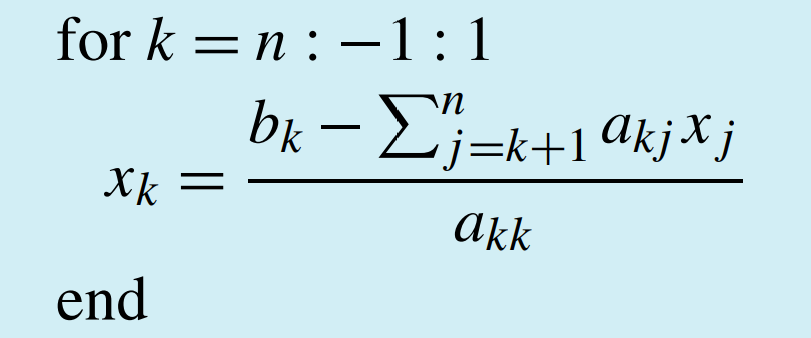
_images/23.png

In the file GE.m, you will find the outlines of MATLAB functions. Modify them to apply these algorithms.

Now you can run project5.m, and you should see the following output:

Matrix A =
     2     1    -1
     4     0    -1
    -8     2     2

Vector b =
     6
     6
    -8

Running GE.m ...
Solution vector x =
     1
     2
    -2

\(x\) is the solution of linear system

\[\begin{split} \begin{array}{ccccccl} 2x_1 & + & x_2 & - & x_3 & = & 6 \\ 4x_1 & & & - & x_3 & = & 6 \\ -8x_1 & + & 2x_2 & + & 2x_3 & = & -8 \end{array} \end{split}\]

Part 2 - Gaussian Elimination with partial pivoting#

If you run the code of part 2, you will see the following output:

Part 2: Gaussian Elimination with pivoting
Matrix A =
    6.0000    2.0000    2.0000
    2.0000    0.6667    0.3333
    1.0000    2.0000   -1.0000

Vector b =
    -2
     1
     0

If we use Gaussian Elimination without pivoting, we will have wrong answer:
Running GE.m ...
Solution vector x =
   NaN
   NaN
   NaN

That is, if we use Gaussian Elimination without pivoting to solve linear system

\[\begin{split} \begin{array}{ccccccl} 6x_1 & + & 2x_2 & + & 2x_3 & = & -2 \\ 2x_1 & + & \frac{2}{3}x_2 & + & \frac{1}{3}x_3 & = & 1 \\ x_1 & + & 2x_2 & - & x_3 & = & 0 \end{array} \end{split}\]

it will not get the right solution. The reason is \(a_{22}\) becomes 0 at the second step of elimination. We need partial pivoting! Now complete the code in GEpivot.m to add pivoting in Gaussian Elimination. Then you will have the following output:

Running GEpivot.m ...
Solution vector x =
    2.6000
   -3.8000
   -5.0000

We get the solutions!

Hint

  • How could I find the maximum absolute value and corresponded index in a partial column of matrix?

    Suppose we have a \(4\times4\) matrix A as follows,

    \[ \require{color} % required for color properties \newcommand{\highlight}[1]{\colorbox{pink}{$#1$}} \]
    \[\begin{split} A=\begin{bmatrix} -3& 2& 1& 1\\ 2& \highlight{1}& 3& 4\\ 3& \highlight{4}& 5& 2\\ -1& \highlight{2}& 3& 2 \end{bmatrix} \end{split}\]

    and we type it in MATLAB:

    >> A =[-3 2 1 1;   2 1 3 4;   3 4 5 2;   -1 2 3 2]

    Now suppose we want to find the index of maximum absolute value in the partial of column 2, say row 2 to row 4 (the highlighted part), then we can run the following code:

    >> [val,q]=max(abs(A(2:4,2)))

    val and q are outputs of the built-in function max. val is the maximum absolute value and q is the index of val in the partial column. On the right side, 2:4 use the colon operator to specify the row 2 through row 4 of the matrix A, the 2 after the comma specify the column 2 of the matrix A. So you will have the following result:

    val = 
    4
q =
    2

    This means the second element in the partial column has maximum absolute value, which is 4.

    But we need to know the position of this number in the whole matrix, so we need to convert the q to global index value:

    >> q=q+2-1
q = 
    3

    The 2 on the right side represents the first row in the partial column is the second row of the whole column. Now we have the global q value is 3.

  • How could I swap two rows in a matrix?

    Now suppose you want to swap the second and third rows of A, you can use the following code:

    >> A([2,3],:)=A([3,2],:)

Part 3 - (Optional) Backslash operation “\”#

This part gives you practice with backslash operation in MATLAB.

For a linear system \(Ax=b\) with a nonsingular square matrix A, the solution x can be found through the backslash operation:

x=A\b

Now let’s use this operation to solve the system

\[\begin{split} \begin{array}{ccccccl} 6x_1 & + & 2x_2 & + & 2x_3 & = & -2 \\ 2x_1 & + & \frac{2}{3}x_2 & + & \frac{1}{3}x_3 & = & 1 \\ x_1 & + & 2x_2 & - & x_3 & = & -2 \end{array} \end{split}\]

Writing this system in matrix format \(Ax=b\) yields

\[\begin{split} A=\begin{bmatrix} 6 & 2 & 2 \\ 2 & \frac{2}{3} & \frac{1}{3} \\ 1 & 2 & -1 \end{bmatrix},\ \ b=\begin{bmatrix} -2\\ 1\\ -2 \end{bmatrix}, \end{split}\]

Now type matrix A and column vector b and backslash operation as following command window:

A = [6 2 2
     2 2/3 1/3
     1 2 -1];
b = [-2
      1
    -2];
x = A\b

Be careful b must be column vector!

Now it will show you the solution as

x =
    3.0000
   -5.0000
   -5.0000

Part 4 - (Optional) Inverse of a nonsingular matrix#

When the inverse of a nonsingular matrix is needed, a call to the inv function does the work. For a nonsingular matrix A, call

Y = inv(A)

provides the inverse of A. Now type this code in command window, it will show you

Y =
   -1.7778    0.8889   -0.1111
    1.5556   -0.7778    0.2222
   -0.1111    0.2222   -0.1111

The matrix Y is the inverse of A. You can double check it by typing A*Y or Y*A in command window. You will find the product is an identity matrix.

5.3. Submit your code#

This is the last step. You should submit your code files to WTClass. After clicking Browse My Computer, you should select all files listed in Introduction to upload. Failure to do so will affect your grade.

Contents