Project:Truncation Error

2. Project:Truncation Error#

2.1. Introduction#

In this project, you will use Taylor polynomials to approximate functions and find truncation errors.

Recall the n-th Taylor polynomial for \(f\) about \(x_0\) is

\[ P_n(x)=f(x_0)+f'(x_0)(x-x_0)+ \frac{f''(x_0)}{2!}(x-x_0)^2+\cdots+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n \]

To get started with this project, you will need to download the starter code and unzip its contents to the directory where you wish to complete the project.

Files included in this project

  • project2.m - Script that steps you through the project.

  • checkMyAnswer.m - Script that checks your code.

  • checkMyAnswer.mat - Data set.

  • data.mat - Data set.

  • * thirdTaylorPolyExp.m - Third Taylor polynomial of \(f(x)=e^x\) at \(x=0\).

  • * errors.m - Absolute and relative errors.

  • * nthTaylorPolyExp.m - nth Taylor polynomial of \(f(x)=e^x\) at \(x=0\).

You need to complete the files with *.

Throughout the project, you will be using the script project2.m. This script set up all dataset for the problem and make calls to functions that you will write. Do not modify it. You are only required to modify functions in * files, following the instructions in this project.

2.2. Assignments#

Part 1 - Taylor polynomials of exponential function#

The first part of project2.m gives you practice with function in MATLAB. In the file thirdTaylorPolyExp.m, you will find the outline of a MATLAB function. Modify it to return the 3rd Taylor polynomial of \(f(x)=e^x\) at \(x=0\), i.e.,

\[ y=1+x+\frac{x^2}{2!}+\frac{x^3}{3!} \]

Hint

  • In MATLAB, there is a built-in function factorial(n) to return \(n!\). You can use it directly or you can calculate factorial by hand to simplify the formula above.

  • This function should work for both scalar \(x\) and vector \(\mathbf{x}\). Check your code and use the proper element-by-element operators.

Once complete, run project2.m. You should see output similar to the following:

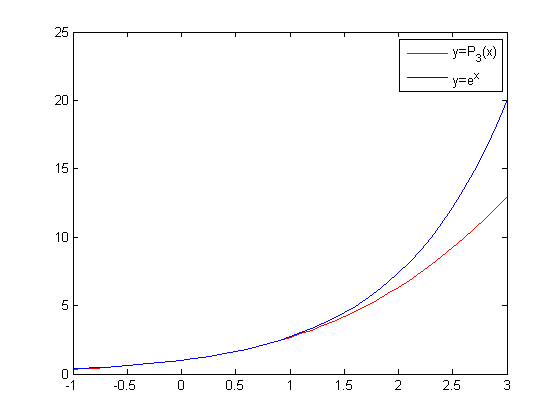
_images/11.png

Part 2 - Absolute and relative errors#

In this section we denote the true and approximate values of a quantity by \(x\) and \(x^*\), respectively. Then we write absolute error absError and relative error relError as

\[\begin{split} \begin{aligned} absError&=\left|x-x^*\right|\\ relError&=\frac{\left|x-x^*\right|}{|x|} \end{aligned} \end{split}\]

You need to modify the file errors.m to implement above formulas in MATLAB code.

Hint

  • Use the built-in function abs() to get the absolute values.

  • When you write this code, be carefule about x and x_star - they could be values or vectors. Use element-by-element operations when necessary.

Once complete, run project2.m. This part will use your function to calculate the absolute and relative errors using third Taylor polynomial at \(x=0\) to approximate \(y=e^x\). You should see output as follows:

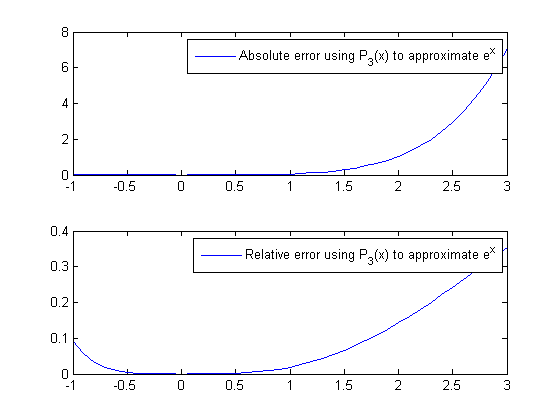
_images/21.png

Part 3 - nth Taylor polynomials#

In this part of project, you need to modify the file nthTaylorPolyExp.m to return the n-th Taylor polynomial of \(f(x)=e^x\) at \(x=0\). Recall this polynomial is

\[ y=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+ \cdots +\frac{x^n}{n!} \]

Hint

  • Use for loop to express the sum. The structure will be similar to the for loop code in Project 1.

  • x could be a vector, so use element-by-element operator if applicable.

  • Use the build-in function factorial(i) to calculate the factorial of i.

Once complete, run project2.m. You should see output similar to the following:

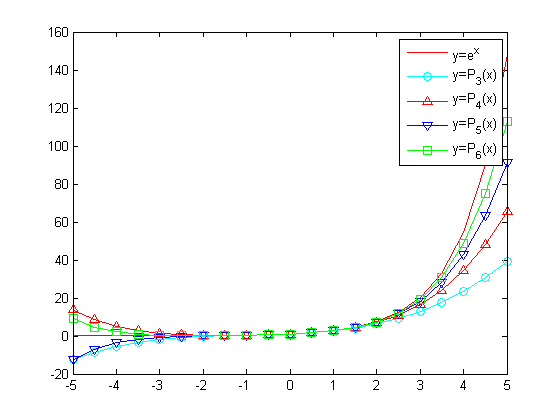
_images/31.png

2.3. Submit your code#

This is the last step. You should submit your code files to WTClass. After clicking Browse My Computer, you should select all files listed in Introduction to upload. Failure to do so will affect your grade.

Contents