Project: Newton’s Method and Secant Method

4. Project: Newton’s Method and Secant Method#

4.1. Introduction#

In this project, you will use Newton’s method and secant method to find the root of equation \(e^{-x}=\sin{x}\) accurate to within \(\epsilon=10^{-10}\). To get started with this project, you will need to download the starter code and unzip its contents to the directory where you wish to complete the project.

Files included in this project

  • project4.m - MATLAB script that steps you through the project.

  • checkMyAnswer.m - MATLAB script that checks your code.

  • checkMyAnswer.mat - Data set.

  • data.mat - Data set.

  • * f.m - Function f(x) to find the root.

  • * fp.m - The derivative of f(x), which will be used in Newton method.

  • * newton.m - Newton method

  • * secant.m - Secant method.

You need to complete the files with *.

Throughout the project, you will be using the script project4.m. This script set up all dataset for the problem and make calls to functions that you will write. Do not modify it. You are only required to modify functions in * files, following the instructions in this project.

4.2. Assignments#

Part 1 - Define functions#

In this project, you will implement Newton’s method in MATLAB. Before coding Newton’s method, complete the functions f.m and fp.m. The f.m file should return the function \( f(x) = e^{-x} - \sin{x} \), while the fp.m file should return its derivative \( f'(x) = -e^{-x} - \cos{x} \). Afterward, run project4.m to visualize the graph of \( f(x) \).

Part 2 - Newton’ Method#

From the graph, you can observe that the root is approximately 0.5, so the initial guess \( x_0 = 0.5 \) is provided in project4.m, and you do not need to modify it.

Then go to the file newton.m and you need to complete the code to return the root of the function of \(f(x)\) by Newton’s method. Note that the iteration formula of Newton’ formula is:

\[ x_{k+1}=x_k-\frac{f(x_k)}{f'(x_k)},\ \ k=0,1,2,... \]

The following flowchart can help you understanding the process.

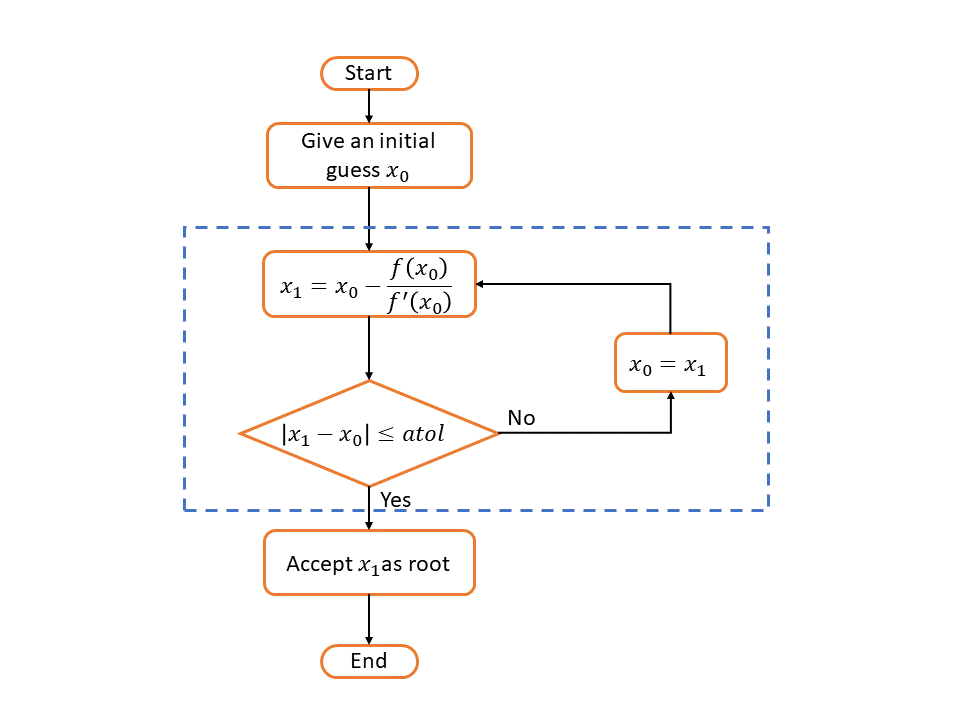
_images/13.png

Hint

  • Use a for loop or while loop to implement the cycle in the blue rectangle.

  • If you use for loop, after accepting x1 as root, do not forget use a break keyword to escape the loop.

Once complete, run project4.m. It will use Newton’s method to find the root of \(f(x)=e^{-x}-\sin{x}\), i.e. the root of \(e^{-x}=\sin{x}\). You should see the following output:

The root of e^(-x)=sin(x) solved by Newton Method is 0.5885327439819

Part 3 - Secant Method#

In this part you will practice secant method in MATLAB. Notice that secant method need two initial guesses. By the graph of \(f(x)\), we choose \(x_0=0.5, x_1=1.0\). These values are given in project4.m and you don’t need to modify it.

In the file secant.m, you should modify it to return the root of the function of \(f(x)\) by secant method. Recall that the iteration formula of secant method is

\[ x_{k+1}=x_k-f(x_k)\cdot\frac{x_k-x_{k-1}}{f(x_k)-f(x_{k-1})}, \ \ \ \ k=1,2,... \]

The following flowchart can help you understanding the process.

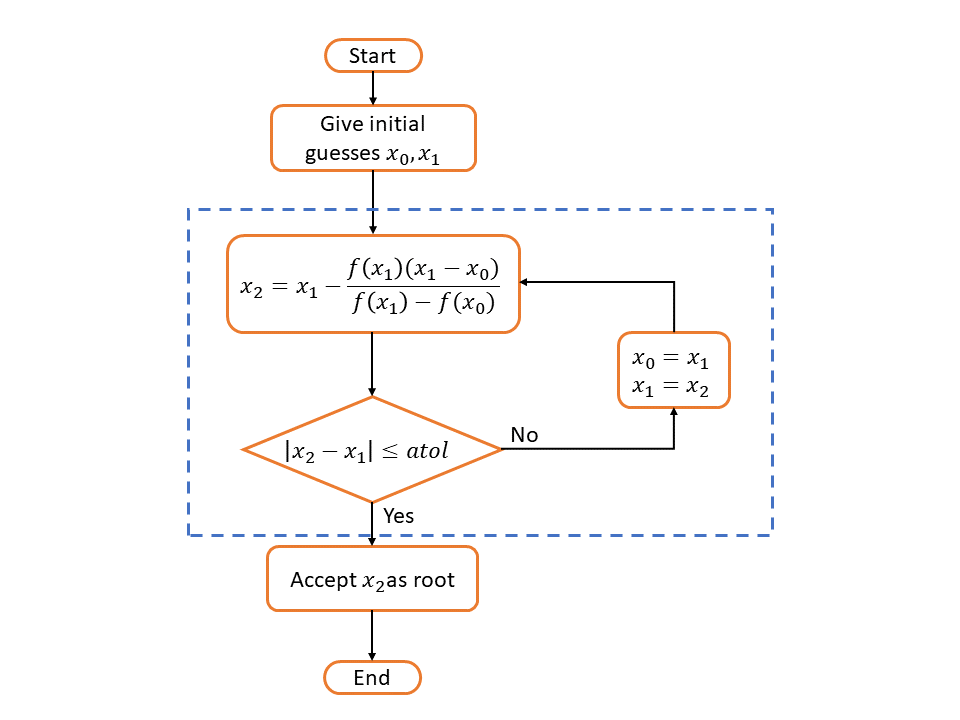
_images/22.png

Hint

  • Use a for loop or while loop to implement the cycle in the blue rectangle.

  • If you use for loop, after accepting x2 as root, do not forget use a break keyword to escape the loop.

Once complete, run project4.m. You should see output:

The root of e^(-x)=sin(x) solved by Secant Method is 0.5885327439819

Part 4 - (Optional) The MATLAB Function fzero#

In this part of project, you don’t need to modify anything. You can type help fzero in MATLAB command window to get details of fzero.

fzero is a root-finding routine in MATLAB and it uses ideas involved in the bisection method and the secant method. As with many MATLAB programs, there are several possible calling sequences. The command

root = fzero(f_name,[a, b])

produces a root within \([a,b]\), where it is assumed that \(f(a)f(b)\le 0\). The command

root = fzero(f_name, x0)

tries to find a root of the function near \(x_0\). The default error tolerance is the maximum precision of the machine, although this can be changed by the user. This is an excellent root-finding routine, combining guaranteed convergence with high efficiency.

Now you can type

root = fzero(@f,[0.5, 1])

in MATLAB command window, then you will get

root =

    0.5885

You may try root = fzero(@f,0.5) to get similar result.

4.3. Submit your code#

This is the last step. You should submit your code files to WTClass. After clicking Browse My Computer, you should select all files listed in Introduction to upload. Failure to do so will affect your grade.

Contents