College Algebra
Tutorial 33: Practice Test on Tutorials 25 - 32
 Learning Objectives
After completing this tutorial, you should be able to:
- Take a test on topics covered in tutorials 25 - 32 in
this website.
|
Special Notes about Tutorial 33:
-
I can not guarantee
you will pass
your test after going though any of the tutorials in this website or
this
practice test. However, it will definitely help you to better
understand
the topics covered better.
-
Disclaimer: WTAMU and Kim Seward are not
responsible
for how a student does on any test or any class for any reason
including
not being able to access the website due to any technology
problems.
-
There are no videos on this page. To view videos on the type of problems found on this page, please go to the tutorial (25 - 32) that corresponds with that problem.
|
Introduction
It
is important to note that, chances, are I'm not your math instructor. You need to check with your math teacher as to things like when your
next math test is and what it covers. It may cover more material
on the test than what is in this practice test. Just note that
there are other practice tests at this website. So, after finding out what
is on your test (if you have one) do the practice test(s) problems that
go with the test you are preparing for. If you are not in a class
or are not having a test soon, this practice test is still good practice
to go through and check to make sure you are understanding this material
before moving on - kind of like a spot check. The material on this
practice test goes with Tutorial 25:
Slope of a Line, Tutorial
26: Equations of Lines, Tutorial
27: Graphing Lines, Tutorial
28: Parallel and Perpendicular Lines, Tutorial
29: Circles, Tutorial
30: Introduction to Functions, Tutorial
31: Graphs of Functions, Part I, Tutorial
32: Graphs of Functions, Part II.
Also note that your teacher may word the problems on their test a
little differently, may have some different kinds of problems, or may have
a different number of problems than what is in this practice test.
Again, since I'm probably not your math instructor, I don't know exactly
how your teacher will set up your math test. Just note that these
problems will help you build an understanding of the concepts presented
and the terms used in math problems. If you have an understanding
of the problems instead of just memorizing them, then you should do fine
on these concepts, no matter how the test is set up.
|
Steps to Studying for a Math Test
|
-
Work through problems. If you are in a class, you should have
done this on completion of any homework you have done. For anyone,
you can accomplish this by doing the practice problems found in each tutorial.
-
Check work on problems. The practice problems in each tutorial
have links to the answers to them so you can instantly check how you are
doing. Also, in most math books, the odd answers are found in the
back of the book.
-
Review concepts. Whether you got the problems right or wrong,
make sure you review over them. If you did get a problem wrong, make
sure you either review that concept in it's respective tutorial or ask
your math teacher about it. If you don't ask about a problem before
a test, you are going to kick yourself when it comes up on the test.
-
Work through problems as if you were taking the test - no notes, book,
webpages, etc. This practice test is a perfect way to do that. After
taking this practice test, check your answers by clicking on the link to
the answer key found at the bottom of the practice test (before the 'need
extra help on these topics' section)
|
|
It is to your benefit to show as much of the work as
possible on
the problems that have several steps involved.
Make sure that you read the directions carefully,
you wouldn't
believe how many points get taken off math tests for people not
following
directions.
Pace yourself. You do not have to be the
first one done
to do well on the test. Do not panic if there is still time left
to take the test and others are turing it in. Sometimes that
means
they do not know the material and left some of the answers blank.
Do not worry about anyone else but yourself.
Don't rush through a problem.
Another thing that
math teachers take points off for are careless mistakes made by people
that rush through a problem. When those students get their tests
back, they bonk themselves on the head at some of the things that got
counted
wrong, things that they knew how to do.
Check your answers. If you have time, go
back and check
your answers.
Remember to breathe!!!! I know some of you
are scared to
death at the thought of having to take a math test of any kind.
For
you guys, try to relax and don't forget to breathe. (Even if you
aren't scared to take a math test, it is probably a good idea to
remember to breathe, I wouldn't want you to pass out during the
test). If it feels like your brain has left the building during
your test,
just close your eyes and breathe in and out and in and out and your
brain
will return.
Good luck on your test. If you are taking a
math test soon,
don't panic, you are going to do great!!! |
Practice Test
Problems 1a - 1c: Find the slope of the straight line that
passes through the given points or state that the slope is undefined.
Then indicate if the line through the points rises (left to right), falls
(left to right), is horizontal, or is vertical. |
1a. (7, 4) and (1, 1) |
1b. (-3, 4) and (2, -1) |
Problems 2a - 2d: Write an equation for the line in point/slope
form and slope/intercept form that has the given condition. |
2a. Slope = 3/2 and passes through the origin. |
2b. x-intercept = 4 and y-intercept
= -3 |
2c. Passes through (3, 2) and is parallel to  . |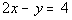
2d. Passes through (-1, -1) and is perpendicular to  . |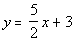
Problems 3a - 3d: Give the slope and y-intercept
of the given line and then graph it. |
3a.  |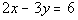
3b.  |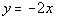
3c.  |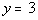
3d.  |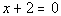
Problems 4a - 4b: Find the slope of the line that is a) parallel
and b) perpendicular to the given line. |
4a.  |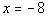
4b.  |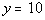
Problem 5a: Write the standard form of the equation of the circle
with the given center and radius. |
5a. center (-2, 0) and r = 3 |
Problem 6a: Find the center and radius of the given circle
and graph it. |
6a.  |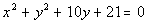
Problems 7a - 7b: Determine if the given relation is function
or not. Give its domain and range. |
7a. {(-1, 2), (1, 3), (-1, 4), (2, 5)} |
7b. {(1, 1), (2, 2), (3, 3), (4, 4)} |
Problems 8a - 8b: Decide whether y is a function of x. |
8a.  |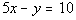
8b.  |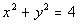
Problem 9a: Find and simplify a) f(a),
b) f(a + h)
and c)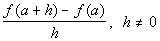 
using the given function. |
9a.  |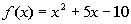
Problem 10a: Find the functional values f(-5), f(1),
and f(3) for the compound function. |
10a.  |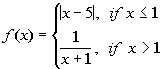
Problems 11a - 11c: Give the domain of the function. |
11a.  |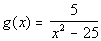
11b.  |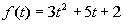
11c.  |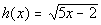
Problems 12a - 12e: Graph the given function using the given
values of x. Also use the graph
to determine the domain and range of the function. |
12a. 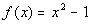 ; x = -3, -2, -1, 0, 1, 2, 3 |
12b. 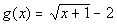 ; x = -1, 0, 3, 8 |
12c. 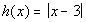 ; x = 0, 1, 2, 3, 4, 5, 6 |
12d. 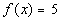 ; x = -3, -2, -1, 0, 1, 2, 3 |
12e. 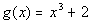 ; x = -2, -1, 0, 1, 2 |
Problem 13a: Use the graph to determine a) the x-intercepts,
if any b) the y-intercept, if any, c) the functional value indicated, to
determine intervals on which the function is d) increasing, if any, e)
decreasing, if any, and f) constant, if any. |
13a.
|
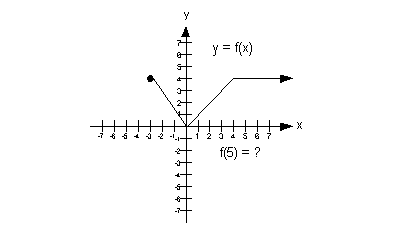
Problems 14a - 14b: Use the vertical line test to identify
graphs in which y is a function of x. |
14a.
|
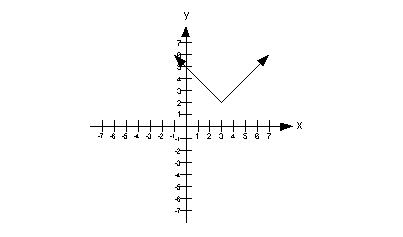
14b.
|
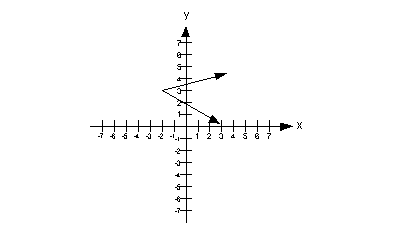
Problems 15a - 15b: Determine if the given function is even,
odd or neither. |
15a.  |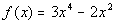
15b.  |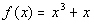
Problem 16a: If f(x)
= int(x), find the given functional value. |
Need Extra Help on these Topics?
Last revised on July 3, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward.
All rights reserved.
|
|
