College Algebra
Tutorial 29: Circles
 Learning Objectives Learning Objectives
After completing this tutorial, you should be able to:
- Write the equation of a circle in standard form given
the radius and
center.
- Write the equation of a circle in standard form given
the equation
written
in general form.
- Determine what the center and radius of a circle are
given the equation
of the circle.
- Graph a circle.
|
 Introduction Introduction
In this tutorial we get to look at circles. We
will discuss how
to write an equation in standard form given either the radius and
center
or the equation written in general form. We will revisit the idea
of completing the square to help us go from the general form to the
standard
form of the equation of the circle. If you need a review on
completing
the square, feel free to go to Tutorial
17: Quadratic Equations. We will also look at how to find
the center ahd radius of a circle when looking at the equation of
it.
And the fun part, we get to graph these circles too. I guess you
better get to it. |
 Tutorial Tutorial
|
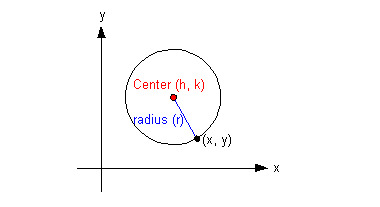
The Standard Form of the
Equation of a Circle
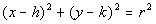
(h, k)
is
the center
r is the radius
(x, y)
is
any point on the circle
|
All points (x, y)
on the circle are a fixed distance (radius) away from the center (h, k).
The h value of
your center is the first value of your ordered pair and the k value of your center is the second value of your ordered pair. |
We can use this form to plug into when we need to
come up with the
equation of a circle.
When writing an equation of a circle, keep in mind that you
ALWAYS need two pieces of information:
- The center of the circle.
- The radius of the circle.
Once you have these two pieces of
information,
you plug the h and k values from your center and the value of the radius (r)
into the standard form of the equation of a circle. |
 Example
1: Example
1: Write the standard form of the equation of the circle
with
center (5, 7) and r = 4. |
What are the two things we need to write an equation
of a circle????
If you said the center and the radius, you are correct.
Looks like we have all the information we need. We
are ready to
put our equation together.
What value are we going to
replace h with?
If you said 5, you are correct!!! h is the first number of the ordered pair of the center of the circle.
What value are we going to
replace k with?
If you said 7, you are right on!!! k is the second number of the ordered pair of the center of the circle.
What value are we going to
replace r with?
If you said 4, give yourself a pat on the back!!! r is the radius of the circle.
Putting it into standard form
we get: |
|
*Plug in 5 for h,
7 for k, and 4 for r
*4 squared is 16
*Standard form of circle with
center (5, 7)
and radius 4
|
|
|
 Example
2: Example
2: Write the standard form of the equation of the circle
with
center (-3, -1) and 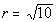 . |
What are the two things we need to write an equation
of a circle????
If you said the center and the radius, you are correct.
Looks like we have all the information we need. We
are ready to
put our equation together.
What value are we going to
replace h with?
If you said -3, you are correct!!! h is the first number of the ordered pair of the center of the circle.
What value are we going to
replace k with?
If you said -1, you are right on!!! k is the second number of the ordered pair of the center of the circle.
What value are we going to
replace r with?
If you said square root of 10, give yourself a pat on the back!!! r is the radius of the circle.
Putting it into standard form
we get: |
|
*Plug in -3 for h,
-1 for k, and sq. root of 10 for r
*sq. root of 10 squared is 10
*Standard form of circle with
center (-3,-1)
and radius of sq. root of 10
|
Make sure that you are careful
when one of
your values is negative and you have to subtract it as we did in line
2. x - (-3) is not the same as x - 3 and y - (-1) is not the same as y - 1. |
 Example
3: Example
3: Write the standard form of the equation of the circle
with
center (0, 0) and r = 10. |
What are the two things we need to write an equation
of a circle????
If you said the center and the radius, you are correct.
Looks like we have all the information we need. We
are ready to
put our equation together.
What value are we going to
replace h with?
If you said 0, you are correct!!! h is the first number of the ordered pair of the center of the circle.
What value are we going to
replace k with?
If you said 0, you are right on!!! k is the second number of the ordered pair of the center of the circle.
What value are we going to
replace r with?
If you said 10, give yourself a pat on the back!!! r is the radius of the circle.
Putting it into standard form
we get: |
|
*Plug in 0 for h,
0 for k, and 10 for r
*10 squared is 100
*Standard form of circle with
center (0, 0)
and radius 10
|
Generally, when you have an expression where you are
subtracting 0,
you can simplify it by not writing the - 0. Going from line 2 to
3 above, I simplified the expression x -
0
by writing it in the equivalent form x and then squaring it, it
becomes 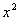 .
Similarly, I wrote y - 0 as y and then squaring it, it
becomes 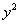 . |
|
The General Form of the Equation
of a Circle
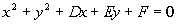
|
Finding the Center and
Radius
of a Circle Given its Equation
|
If your equation is in standard form it will make it
easier for you
to identify the center and radius.
If your equation is in the general
form you will need to complete the square to both the x terms and the y terms as if they were
two separate
problems.
Below is a review on completing the square. If you
need more of
a review on this topic, feel free to go to Tutorial
17: Quadratic Equations. |
Step 1a: Make
sure that the coefficients on the 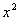 and and 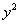 terms
are equal
to 1. terms
are equal
to 1. |
If the coefficient of 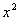 and and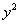 are are already 1, then proceed to step 1b.
If the coefficient is not equal to 1, then divide both
sides by the
coefficients of the 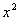 and and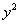 squared terms. squared terms. |
Step 1b: Isolate
the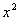 , x, , x, 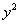 and y terms. and y terms. |
In other words, rewrite it so that the 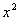 ,
x, ,
x, 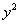 and
y terms and
y terms are all on one side and the constant is on the
other
side. |
Step 1c: Complete
the square for both x and y. |
At this point we will be creating a perfect square
trinomial for the x terms
as well as the y terms. Recall
that a
perfect square trinomial (PST) is of the form 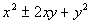 and
it factors in the form 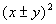 .
When it is in that form it will allow us to continue onto the next step
and write the equation in standard form, 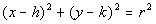 .
We need to find a number that we can add to the 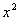 and x terms so that we have a PST.
We
also need to find a number that we can add to the and x terms so that we have a PST.
We
also need to find a number that we can add to the 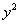 and y terms so that we have a PST. We can get that magic number
by
doing the following: and y terms so that we have a PST. We can get that magic number
by
doing the following:
If we have 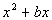 we
complete its square by adding we
complete its square by adding 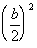 to
both sides of the equation. to
both sides of the equation.
In other words, we complete the square by taking
½ of b (the
coefficient of the x term) and then
squaring
it. Make sure you remember to add it to BOTH sides to keep the
equation
balanced. We do the same type of thing with the 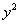 and y terms. and y terms.
Since we will be completing the square for both the x’s and the y’s, we
will have
two numbers that we will be adding to both sides. |
Step 1d: Factor
both PST’s created in step 1c as a binomial squared. |
This will put the equation of the circle in standard
form, 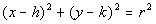 . |
Step 2: Identify
the center and radius of circle. |
You can do this by lining up the equation found in step
1 with the
standard form of the equation of a circle. |
Step 3: Graph,
if needed. |
This step isn't really part of finding the center or
the radius.
But in some cases you will need to graph your circle after finding
those
two items. You can graph your circle by plotting your center (h, k)
and then using your radius to find points on the circle. All
points
(x, y) on
the circle
are a fixed distance (radius) away from the center (h, k). Then, draw your circle. Keep in mind that when we use the letters h and k for our center, h is the first value of the ordered pair of the center. In other
words,
when you graph it, it corresponds to the x-axis. k is the second value of the ordered pair of the center. In other
words,
when you graph it, it corresponds to the y-axis. |
 Example
4: Example
4: Find the center and radius of the circle, 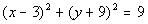 ,
and graph it. |
The equation is already in standard form. |
|
*Standard form of circle
*9 is 3 squared
|
Make sure that you are
careful. The
original standard form is 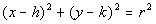 ,
where we have x MINUS h and y MINUS k.
So h is the number that we are
subtracting
from x and k is
the number that we are subtracting from y.
Also, the right side of the equation is r SQUARED. ,
where we have x MINUS h and y MINUS k.
So h is the number that we are
subtracting
from x and k is
the number that we are subtracting from y.
Also, the right side of the equation is r SQUARED.
So, in line 2 above, I rewrote
the equation
to show what numbers we were actually subtracting on the left side of
the
equation.
On the right side of the
equation I showed
what number was being squared. This is to help you see how we get
the center (h, k)
and the radius (r).
Make sure that you are careful
when one of
your values is negative and you have to subtract it as we did in line
2. y - (-9) is not the same as y -
9.
What value is h?
If you said 3, you are correct!!! Since
3 is the value being subtracted from x in the
first ( ), that is the value of h.
What value is k?
If you said -9, you are right on!!! Since
-9 is the value being subtracted from y in
the second ( ), that is the value of k.
What value is r?
If you said 3, give yourself a pat on the back!!! Since 3 is
the number being squared on the right side of the standard form of our
equation, that is the value of r.
The center is (3, -9) and the radius is 3. |
Step 3: Graph,
if needed. |
 Example
5: Example
5: Find the center and radius of the circle, 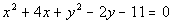 ,
and graph it. |
The coefficients on the 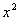 and 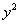 terms
are both
already 1. |
|
*Inverse of sub. 11 is add. 11
|
|
*Complete the square for both x and y
*Make sure that you add 4 and 1 to
BOTH sides |
Completing the square for x (as
shown
above):
b is the coefficient of the 4x term, which in this case is 4. Complete the square by taking 1/2
of b and squaring it. Taking 1/2
of 4
we get 2, and then squaring 2 we get 4.
Completing the square for y (as
shown
above):
b is the coefficient of the -2y term, which in this case is -2. Complete the square by taking 1/2
of b and squaring it. Taking 1/2 of
-2
we get -1, and then squaring -1 we get 1. |
|
*Factor each PST
*Standard form of circle |
|
*Standard form of circle
*16 is 4 squared
|
Make sure that you are
careful. The
original standard form is 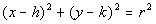 ,
where we have x MINUS h and y MINUS k.
So h is the number that we are
subtracting
from x and k is
the number that we are subtracting from y.
Also, the right side of the equation is r SQUARED. ,
where we have x MINUS h and y MINUS k.
So h is the number that we are
subtracting
from x and k is
the number that we are subtracting from y.
Also, the right side of the equation is r SQUARED.
So in line 2 above, I rewrote
the equation
to show what numbers we were actually subtracting on the left side of
the
equation.
On the right side of the
equation I showed
what number was being squared. This is to help you see how we get
the center (h, k)
and the radius (r).
Make sure that you are careful
when one of
your values is negative and you have to subtract it as we did in line
2. x - (-2) is not the same as x - 2.
What value is h?
If you said -2, you are correct!!! Since
-2 is the value being subtracted from x in
the first ( ), that is the value of h.
What value is k?
If you said 1, you are right on!!! Since
1 is the value being subtracted from y in the
second ( ), that is the value of k.
What value is r?
If you said 4, give yourself a pat on the back!!! Since 4 is
the number being squared on the right side of the standard form of our
equation, that is the value of r.
The center is (-2, 1) and the radius is 4. |
Step 3: Graph,
if needed. |
 Example
6: Example
6: Find the center and radius of the circle, 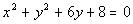 ,
and graph it. |
The coefficients on the 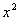 and 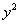 terms
are both
already 1. |
|
*Inverse of add. 8 is sub. 8
|
|
*Complete the square for both x and y
*Make sure that you add 0 and 9 to
BOTH sides |
Completing the square for x (as
shown
above):
Note how we have an x squared term, but
we are missing our x term. If we
are
missing a term then it is understood to be 0. So in this case we
would think of our b, the coefficient in
front
of the x term, as 0. Taking 1/2 of
0
we get 0, and then squaring 0 we get 0.
Completing the square for y (as
shown
above):
b is the coefficient of the 6y term, which in this case is 6. Complete the square by taking 1/2
of b and squaring it. Taking 1/2 of
6
we get 3, and then squaring 3 we get 9. |
|
*Factor each PST
*Standard form of circle
|
Note that since we were only adding a 0 to the x squared term, that we can just write that as 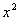 . |
|
*Standard form of circle
*16 is 4 squared
|
Make sure that you are
careful. The
original standard form is 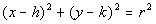 ,
where we have x MINUS h and y MINUS k.
So h is the number that we are
subtracting
from x and k is
the number that we are subtracting from y.
Also, the right side of the equation is r SQUARED. ,
where we have x MINUS h and y MINUS k.
So h is the number that we are
subtracting
from x and k is
the number that we are subtracting from y.
Also, the right side of the equation is r SQUARED.
So in line 2 above, I rewrote
the equation
to show what numbers we were actually subtracting on the left side of
the
equation.
On the right side of the
equation I showed
what number was being squared. This is to help you see how we get
the center (h, k)
and the radius (r).
Make sure that you are careful
when one of
your values is negative and you have to subtract it as we did in line
2. y - (-3) is not the same as y - 3.
What value is h?
If you said 0, you are correct!!! Since
there is no value being subtracted from x in
the first ( ) that means it is understood that 0 is the number
being
subtracted, that is the value of h.
What value is k?
If you said -3, you are right on!!! Since
-3 is the value being subtracted from y in
the second ( ), that is the value of k.
What value is r?
If you said 1, give yourself a pat on the back!!! Since 1 is
the number being squared on the right side of the standard form of our
equation, that is the value of r.
The center is (0, -3) and the radius is 1. |
Step 3: Graph,
if needed. |
 Practice Problems Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1b: Write the standard form of the
equation of the
circle with the given conditions. Practice
Problems 1a - 1b: Write the standard form of the
equation of the
circle with the given conditions.
 Practice
Problems 2a - 2b: Find the center and radius of
the given circle and graph it. Practice
Problems 2a - 2b: Find the center and radius of
the given circle and graph it.
 Need Extra Help on these Topics? Need Extra Help on these Topics?

Last revised on Feb. 26, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.
|
|


