College Algebra
Tutorial 32: Graphs of Functions, Part II:
Domain/Range, Vertical Line Test, Increasing/Decreasing/Constant Functions, Even/Odd Functions, and Greatest Integer Function
 Learning Objectives
After completing this tutorial, you should be able to:
- Determine the domain and range of a function given a
graph.
- Use the vertical line test to determine if a graph is
the graph of a
function
or not.
- Determine the intervals on which a function is
increasing, decreasing
or
constant by looking at a graph.
- Determine if a function is even, odd, or neither by
looking at a graph.
- Determine if a function is even, odd, or neither
given an equation.
- Apply the greatest integer function to any given
number.
|
Introduction
In this tutorial we will take a close look at several
different aspects
of graphs of functions. First we will look at finding the domain
and range of a function given a graph. Next I will show you how a
vertical line can help us determine if a graph is a graph of a function
or not. Then we will look at what it means for a function to be
increasing,
decreasing or constant. This will be followed by showing you how
to tell if a function is even, odd, or neither given either a graph of
the function or just its assignment. We will finish the
lesson
by taking a peek at the greatest integer function. If you need a
review on the definition of a function, feel free to go to Tutorial
30: Introduction to Functions. Sounds like we have our
work
cut out for us in this lesson. I guess you better get to it. |
Tutorial
Let's start by reviewing some terms associated with
functions and how
they pertain to graphs of a function. |
Recall that the domain is the set of all input values
to which the
rule applies. These are called your independent variables.
These are the values that correspond to the first components of the
ordered
pairs it is associated with. If you need a review on the domain,
feel free to go to Tutorial
30: Introduction to Functions.
On a graph, the domain corresponds to the horizontal
axis. Since
that is the case, we need to look to the left and right to see if there
are any end points to help us find our domain. If the graph keeps going
on and on to the right then the domain is infinity on the right side of
the interval. If the graph keeps going on and on to the left then
the domain is negative infinity on the left side of the
interval.
If you need a review on finding the domain given a graph, feel free to
go to Tutorial 31: Graphs of
Functions,
Part I. |
Recall that the range is the set of all output
values. These
are called your dependent variables. These are the values that
correspond
to the second components of the ordered pairs it is associated
with.
If you need a review on the range, feel free to go to Tutorial
30: Introduction to Functions.
On a graph, the range corresponds to the vertical
axis. Since
that is the case, we need to look up and down to see if there are any
end
points to help us find our range. If the graph keeps going up with no
endpoint
then the range is infinity on the right side of the interval. If
the graph keeps going down then the range goes to negative infinity on
the left side of the interval. If you need a review on finding
the
domain given a graph, feel free to go to Tutorial
31: Graphs of Functions, Part I |
No matter what type of graph that you have, recall
that the x-intercept
is where the graph crosses the x axis.
The word 'intercept' looks like the word
'intersect'. Think
of it as where the graph intersects the x-axis.
If you need more review on intercepts, feel free to go
to Tutorial
26: Equations of Lines. |
No matter what type of graph that you have, recall
that the y-intercept
is where the graph crosses the y axis.
The word 'intercept' looks like the word
'intersect'. Think
of it as where the graph intersects the y-axis.
If you need more review on intercepts, feel free to go
to Tutorial
26: Equations of Lines. |
Recall that the functional value correlates with the
second or y value of an ordered pair.
If you need a review on functional values, feel free to
go to Tutorial
30: Introduction to Functions. |
 Example
1: Use the graph to determine a) the domain, b) the
range,
c) the x-intercepts, if any d) the y-intercept,
if any, and e) the functional value indicated.
|
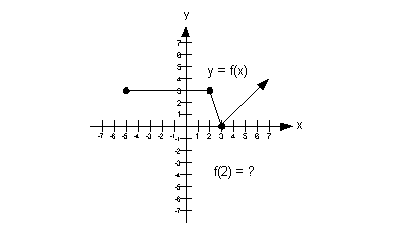
a) Domain
We need to find the set of all input values. In terms of ordered
pairs, that correlates with the first component of each one. In
terms
of this two dimensional graph, that corresponds with the x values
(horizontal axis).
Since that is the case, we need to look to the left and
right and see
if there are any end points. In
this case, note how there is a left endpoint at x = -5 and then the graph goes on and on forever to the right of
-5.
This means that the domain is  . |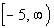
b) Range
We need to find the set of all output values. In terms of ordered
pairs, that correlates with the second component of each one. In terms
of this two dimensional graph, that corresponds with the y values (vertical axis).
Since that is the case, we need to look up and down and
see if there
are any end points. In this case, note how the graph has a low
endpoint
of y = 0 and it has an arrow going up
from
that.
This means that the range is  . |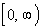
c) x-intercept
If the x-intercept
is where the graph crosses the x-axis,
what
do you think the x-intercept is for this
function?
If you said x = 3
you are correct.
The ordered pair for this x-intercept
would be (3, 0). |
d) y-intercept
If the y-intercept is where the graph
crosses
the y-axis, what do you think the y-intercept
is for this function?
If you said y = 3 you are
correct.
The ordered pair for this y-intercept
would be (0, 3). |
e) Functional
value indicated
If the functional value correlates with the second or y value of an ordered pair what is f(2)?
If you said f(2) = 3 ,
then give yourself
a pat on the back. The functional value at x = 2 is 3.
The ordered pair for this would be (2, 3). |
Example
2: Use the graph to determine a) the domain, b) the
range,
c) the x-intercepts, if any d) the y-intercept,
if any, and e) the functional value indicated.
|
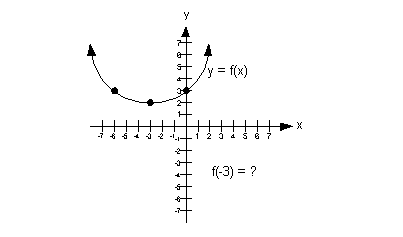
a) Domain
We need to find the set of all input values. In terms of ordered
pairs, that correlates with the first component of each one. In
terms
of this two dimensional graph, that corresponds with the x values
(horizontal axis).
Since that is the case, we need to look to the left and
right and see
if there are any end points. In
this case, note how there are arrows on both ends of the graph and
no end points. This means that the graph goes on and on forever
in
both directions.
This means that the domain is  . |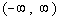
b) Range
We need to find the set of all output values. In terms of ordered
pairs, that correlates with the second component of each one. In terms
of this two dimensional graph, that corresponds with the y values (vertical axis).
Since that is the case, we need to look up and down and
see if there
are any end points. In this case, note how the graph has a low
endpoint
of y = 2 and it has arrows going up from
that.
This means that the range is  . |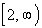
c) x-intercept
If the x-intercept
is where the graph crosses the x-axis,
what
do you think the x-intercept is for this
function?
If you said there is none, you are
right.
Since the graph never crosses the x-axis,
then there is no x-intercept. |
d) y-intercept
If the y-intercept is where the graph
crosses
the y-axis, what do you think the y-intercept
is for this function?
If you said y = 3 you are
correct.
The ordered pair for this y-intercept
would be (0, 3). |
e) Functional
value indicated
If the functional value correlates with the second or y value of an ordered pair what is f(-3)?
If you said f(-3) = 2 ,
then give yourself
a pat on the back. The functional value at x = -3 is 2.
The ordered pair for this would be (-3, 2). |
Example
3: Use the graph to determine a) the domain, b) the
range,
c) the x-intercepts, if any d) the y-intercept,
if any, and e) the functional value indicated.
|
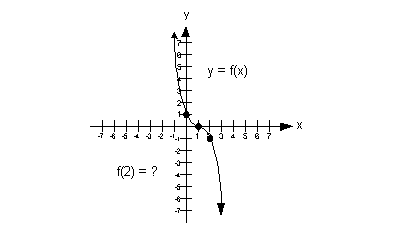
a) Domain
We need to find the set of all input values. In terms of ordered
pairs, that correlates with the first component of each one. In
terms
of this two dimensional graph, that corresponds with the x values
(horizontal axis).
Since that is the case, we need to look to the left and
right and see
if there are any end points. In
this case, note how there are arrows on both ends of the graph and
no end points. This means that the graph goes on and on forever
in
both directions.
This means that the domain is . |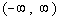
b) Range
We need to find the set of all output values. In terms of ordered
pairs, that correlates with the second component of each one. In terms
of this two dimensional graph, that corresponds with the y values (vertical axis).
Since that is the case, we need to look up and down and
see if there
are any end points. In
this case, note how there are arrows on both ends of the graph and
no end points. This means that the graph goes on and on forever
in
both directions.
This means that the range is . |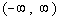
c) x-intercept
If the x-intercept
is where the graph crosses the x-axis,
what
do you think the x-intercept is for this
function?
If you said x = 1
you are correct.
The ordered pair for this x-intercept
would be (1, 0). |
d) y-intercept
If the y-intercept is where the graph
crosses
the y-axis, what do you think the y-intercept
is for this function?
If you said y = 1 you are
correct.
The ordered pair for this y-intercept
would be (0, 1). |
e) Functional
value indicated
If the functional value correlates with the second or y value of an ordered pair what is f(2)?
If you said f(2) = -1 ,
then give yourself
a pat on the back. The functional value at x = 2 is -1.
The ordered pair for this would be (2, -1). |
If no vertical line can be drawn so that it
intersects a graph more
than once, then it is a graph of a function.
Think about it, if a vertical line intersects a graph in
more than one
place, then the x value (input) would
associate
with more than one y value (output), and
you
know what that means. The relation is not a function.
The next two examples illustrate this concept. |
Example
4: Use the vertical line test to identify graphs in which y is a function of x.
|
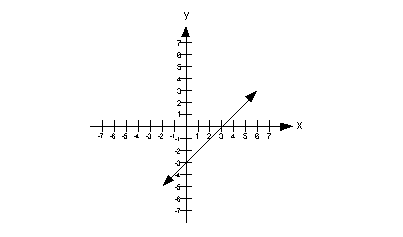
This graph would pass the vertical line test, because
there would not
be any place on it that we could draw a vertical line and it would
intersect
it in more than one place.
Therefore, this is a graph of a function. |
Example
5: Use the vertical line test to identify graphs in which y is a function of x.
|
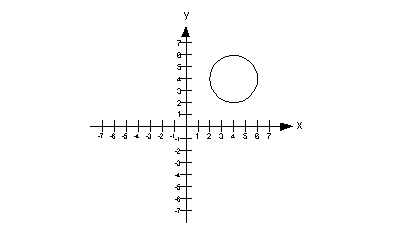
This graph would not pass the vertical line test
because there is at
least one place on it that we could draw a vertical line and intersect
it in more than one place. In fact, there are a lot of vertical
lines
that we can draw that would intersect it in more than one place, but we
only need to show one to say it is not a function.
The graph below shows one vertical line drawn through
our graph that
intersects it in two places: (4, 2) and (4, 6). This shows that
the
input value of 4 associates with two output values, which is not
acceptable
in the function world.
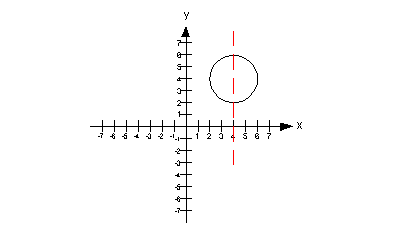
Therefore, this is not a graph of a function. |
In other words, a function is increasing in an
interval if it is
going up left to right in the entire interval.
Below is an example where the function is increasing
over the interval .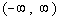
Note how it is going up left to right in the interval .
|
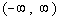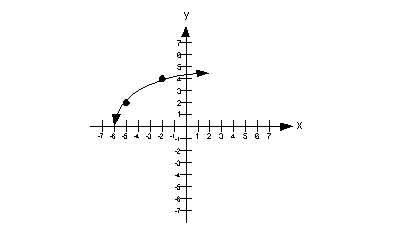
In other words, a function is decreasing in an
interval if it is
going down left to right in the entire interval.
Below is an example where the function is decreasing
over the interval .
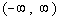Note how it is going down left to right in the interval .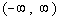
|
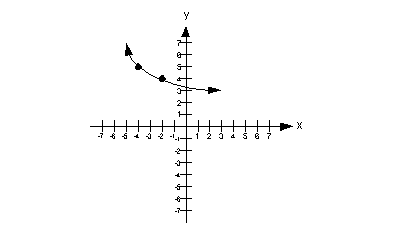
In other words, a function is constant in an
interval if it is horizontal
in the entire interval.
Below is an example where the function is constant over
the interval .
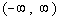Note how it is a horizontal line in the interval .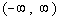
|
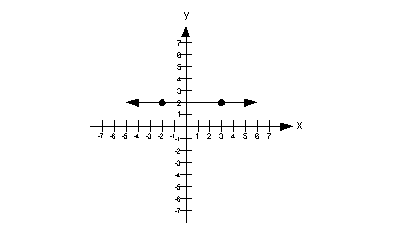
Example
6: Use the graph to determine intervals on which the
function
is a) increasing, if any, b) decreasing, if any, and c) constant, if
any.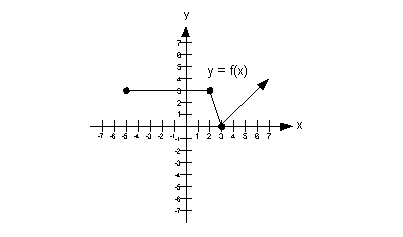
|
a) Increasing
A function is increasing in an interval when it is going up left to
right in that interval? With that in mind, what interval, if any,
is this function increasing?
If you said  ,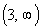
you are correct.
Note how the function is going up left to right,
starting at x = 3 and everywhere to the right of that.
Below shows the part of the graph that is increasing:
|
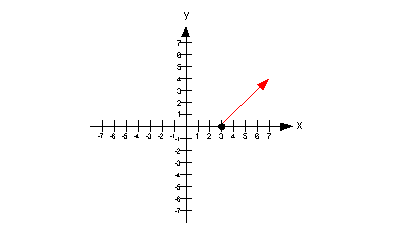
b) Decreasing
A function is decreasing in an interval when it is going down left
to right in that interval? With that in mind, what interval, if
any,
is this function decreasing?
If you said (2, 3), you are right on.
Note how the function is going down left to right from x = 2 to x = 3.
Below shows the part of the graph that is decreasing:
|
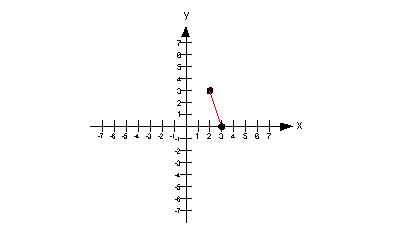
c) Constant
A function is constant in an interval if it is horizontal in the entire
interval. With that in mind, what interval, if any, is this
function
constant?
If you said (-5, 2), pat yourself on the back.
Note how the function is horizontal starting at x = -5 all the way to x = 2.
Below shows the part of the graph that is constant:
|
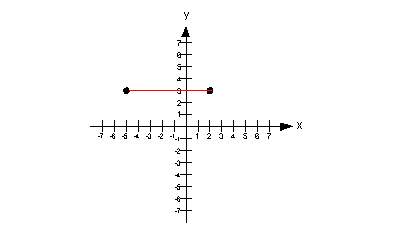
Example
7: Use the graph to determine intervals on which the
function
is a) increasing, if any, b) decreasing, if any, and c) constant, if
any.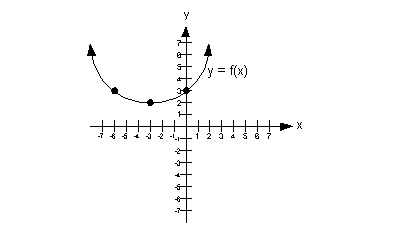
|
a) Increasing
A function is increasing in an interval when it is going up left to
right in that interval? With that in mind, what interval, if any,
is this function increasing?
If you said  ,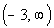
you are correct.
Note how the function is going up left to right,
starting at x = -3 and everywhere to the right of that.
Below shows the part of the graph that is increasing:
|
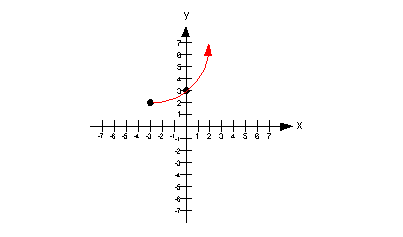
b) Decreasing
A function is decreasing in an interval when it is going down left
to right in that interval? With that in mind, what interval, if
any,
is this function decreasing?
If you said  ,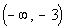
you are right on.
Note how the function is going down left to right from
negative infinity
to x = -3.
Below shows the part of the graph that is decreasing:
|
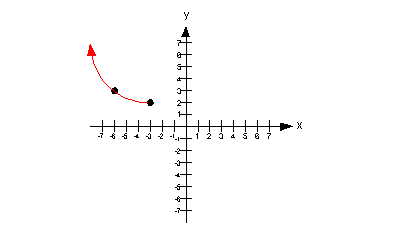
c) Constant
A function is constant in an interval if it is horizontal in the entire
interval. With that in mind, what interval, if any, is this
function
constant?
If you said it is never constant, pat yourself on the
back.
Note how the function is never a horizontal line. |
Example
8: Use the graph to determine intervals on which the
function
is a) increasing, if any, b) decreasing, if any, and c) constant, if
any.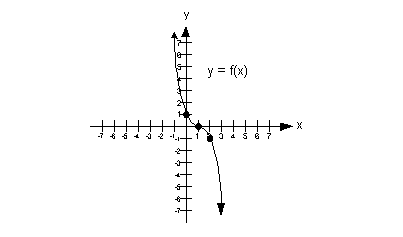
|
a) Increasing
A function is increasing in an interval when it is going up left to
right in that interval? With that in mind, what interval, if any,
is this function increasing?
If you said it never increases, you are correct.
Note how the function never goes up left to right. |
b) Decreasing
A function is decreasing in an interval when it is going down left
to right in that interval? With that in mind, what interval, if
any,
is this function decreasing?
If you said ,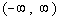
you are right on.
Note how the function is going down left to right from
negative infinity
to infinity.
Below shows the part of the graph that is decreasing:
|
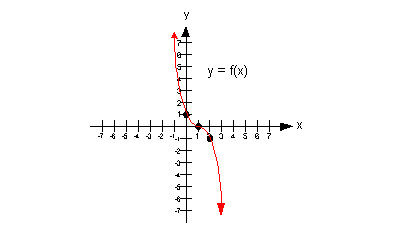
c) Constant
A function is constant in an interval if it is horizontal in the entire
interval. With that in mind, what interval, if any, is this
function
constant?
If you said it is never constant, pat yourself on the
back.
Note how the function is never a horizontal line. |
|
Even Function
A function is even if for all x in the domain
of f
 .
|
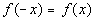In other words, a function is even if replacing x with -x does NOT change the original
function.
In terms of looking at a graph, an even function is
symmetric with respect
to the y-axis. In other words, the
graph
creates a mirrored image across the y-axis.
The graph below is a graph of an even function.
Note how
it is symmetric about the y-axis.
|
|
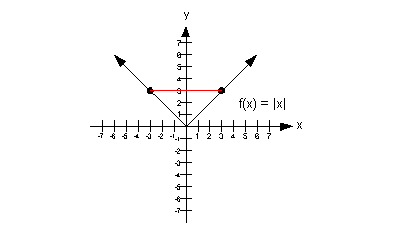
Odd Function
A function is odd if for all x in the domain
of f
 .
|
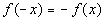In other words, a function is odd if replacing x with -x results in changing every sign of
every
term of the original function.
In terms of looking at a graph, an odd function is
symmetric with respect
to the origin. In other words, the graph creates a mirrored image
across the origin.
The graph below is a graph of an odd function.
Note how
it is symmetric about the origin.
|
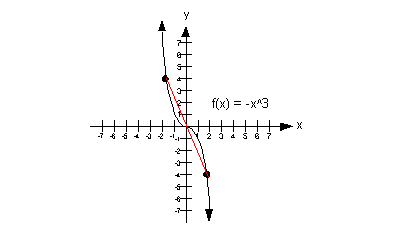
Example
9: Determine if the function 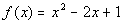 is even, odd or neither. |
To determine if this function is even, odd, or
neither, we need
to replace x with -x and compare f(x)
with f(-x):
|
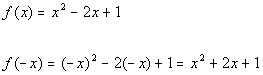
Even?
A function is even if 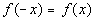for all x in the domain of f.
With that in mind, is this function even?
If you said no, you are
correct. Note how
their second terms have opposite signs, so  . |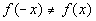
Since we said no for both even and odd, that leaves us
with our answer
to be neither.
Final answer: The function is neither even nor odd. |
Example
10: Determine if the function 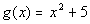 is even, odd or neither. |
To determine if this function is even, odd, or
neither, we need
to replace x with -x and compare g(x)
with g(-x):
|
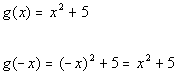
Even?
A function is even if 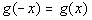 for all x in the domain of g.
With that in mind, is this function even?
If you said yes, you are
correct. Note how
all of the terms of g(x)
and g(-x)
match
up, so .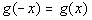
Final answer: The function is
even. |
Example
11: Determine if the function 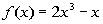 is even, odd or neither. |
To determine if this function is even, odd, or
neither, we need
to replace x with -x and compare f(x)
with f(-x):
|
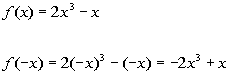
Even?
A function is even if 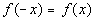for all x in the domain of f.
With that in mind, is this function even?
If you said no, you are
correct. Note how
both of their terms have opposite signs, so . |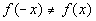
Odd?
A function is odd if 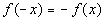for all x in the domain of f.
With that in mind, is this function odd?
If you said yes, you are
right.
Looking at  ,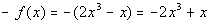
note how all of the terms of f(-x)
and -f(x)
match up, so .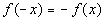
Final answer: The function is
odd. |
|
Greatest Integer Function
int(x)
Greatest integer that is less than or
equal to x.
|
For example, int(5) = 5, int(5.3) = 5, int(5.9) =
5, because
5 is the greatest integer that is less than or equal to 5, 5.3, and
5.9.
The basic graph of the function f(x)
= int(x) is:
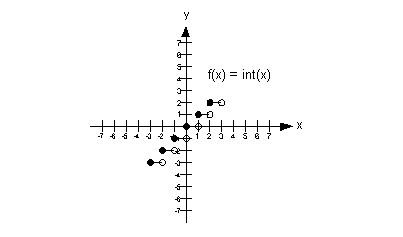
Note how it looks like steps. |
Example
12: If f( x)
= int( x), find the functional value f(7.92). |
We need to ask ourselves, what is the greatest integer
that is less
than or equal to 7.92?
If you said 7, you are correct.
Final answer: 7 |
Example
13: If f( x)
= int( x), find the functional value f(-3.25). |
We need to ask ourselves, what is the greatest integer
that is less
than or equal to -3.25?
If you said -4, you are correct.
Be careful on this one. We are working with a
negative number.
-3 is not a correct answer because -3 is not less than or equal to
-3.25,
it is greater than -3.25.
Final answer: -4 |
Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1b: Use the graph to determine a)
the domain, b)
the range, c) the x-intercepts, if any d) the y-intercept, if any, and
e) the functional value indicated.
Practice
Problems 2a - 2b: Use the vertical line test to
identify graphs
in which y is a function of x.
Practice
Problems 3a - 3b: Use the graph to determine intervals
on which the function
is a) increasing, if any, b) decreasing, if any, and c) constant, if
any.
Practice
Problems 4a - 4b: Use the graph to determine if the
function is even,
odd, or neither.
Practice
Problems 5a - 5c: Determine if the given function is
even, odd or neither.
Practice
Problem 6a: If f(x) = int(x),
find the given
functional value.
Need Extra Help on these Topics?
Last revised on June 18, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.
|
|
and 
in the
interval,
where 
, then 
.
.
.
,
we see that the signs of the first and third terms of f(-x)
and -f(x)
don’t
match, so 
.
