College Algebra
Tutorial 31: Graphs of Functions, Part I:
Graping Functions by Plotting Points
 Learning Objectives Learning Objectives
After completing this tutorial, you should be able to:
- Graph a function by plotting points.
- Determine the domain and range of a function from a graph.
|
 Introduction Introduction
This lesson covers graphing functions by plotting
points as well as
finding the domain and range of a function after it has been
graphed.
Graphs are important in giving a visual representation of the
correlation
between two variables. Even though in this section we are going
to
look at it generically, using a general x and y variable, you can use two-dimensional graphs for any application where
you have two variables. For example, you may have a cost function
that is dependent on the quantity of items made. If you needed to
show your boss visually the correlation of the quantity with the cost,
you could do that on a two-dimensional graph. I believe that it
is
important for you to learn how to do something in general, then when
you
need to apply it to something specific you have the knowledge to do
so.
Going from general to specific is a lot easier than specific to
general.
And that is what we are doing here looking at graphing in general so
later
you can apply it to something specific, if needed. We will also
revisit
the concept of domain and range. This time we will be finding them by
looking
at a graph. We will be using interval notation to write our
answers. In some cases, our domain and/or range will go out
to infinity.
I think that you are ready to go ahead and graph. |
 Tutorial Tutorial
Recall that the domain is the set of all input values
to which the
rule applies. These are called your independent variables.
These are the values that correspond to the first components of the
ordered
pairs it is associated with. If you need a review on the domain,
feel free to go to Tutorial
30: Introduction to Functions.
On a graph, the domain corresponds to the horizontal
axis. Since
that is the case, we need to look to the left and right to see if there
are any end points to help us find our domain. If the graph keeps going
on and on to the right then the domain is infinity on the right side of
the interval. If the graph keeps going on and on to the left then
the domain is negative infinity on the left side of the interval. |
Recall that the range is the set of all output
values. These
are called your dependent variables. These are the values that
correspond
to the second components of the ordered pairs it is associated
with.
If you need a review on the range, feel free to go to Tutorial
30: Introduction to Functions.
On a graph, the range corresponds to the vertical
axis. Since
that is the case, we need to look up and down to see if there are any
end
points to help us find our range. If the graph keeps going up with no
endpoint
then the range is infinity on the right side of the interval. If
the graph keeps going down then the range goes to negative infinity on
the left side of the interval. |
Graphing a Function
by Plotting Points
|
Step 1: Find at
least four ordered pair solutions. |
Functions can vary on what the graph looks like.
So it is good
to have a lot of points so that you can get the right shape of the
graph,
whether it be a straight line, curve, etc.. |
Step 2: Plot the
points found in step 1. |
Here are the basic shapes of some of the more common
graphs of functions.
Keep in mind that these are the
basic shapes
of these graphs. They can be shifted and stretched depending on
the
function given. A major goal is to recognize what type of
function
you are graphing and predict the basic shape from that before you even
start.
Note that the domain and ranges that go with each one
are also given.
|
 Example
1 Example
1: Graph the function 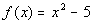 using the given values of x. Also
use
the graph to determine the domain and range of the function. x = -3, -2, -1, 0, 1, 2, 3 |
Step 1: Find at
least four ordered pair solutions. |
I’m going to use a chart to organize my
information. A chart
keeps track of the x values that you are
using
and the corresponding y value found when
you
used a particular x value.
We will use the seven values of x that were
given to find corresponding functional values to give us seven ordered
pair solutions.
Keep in mind that the functional value that we find
correlates to the
second or y value of our ordered pair. |
|
x
|
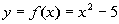
|
(x, y)
|
|
-3
|
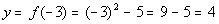
|
(-3, 4)
|
|
-2
|
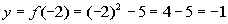
|
(-2, -1)
|
|
-1
|
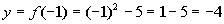
|
(-1, - 4)
|
|
0
|
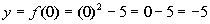
|
(0, -5)
|
|
1
|
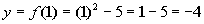
|
(1, - 4)
|
|
2
|
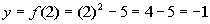
|
(2, -1)
|
|
3
|
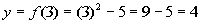
|
(3, 4)
|
Step 2: Plot the
points found in step 1. |
Domain
We need to find the set of all input
values.
In terms of ordered pairs, that correlates with the first component of
each one. In terms of this two dimensional graph, that
corresponds
with the x values (horizontal
axis).
Since that is the case, we need to
look to the
left and right and see if there are any end points. In
this case, note how the curve has
arrows at both
ends, that means it would go on and on forever to the right and to the
left.
This means that the domain
is 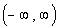 . . |
Range
We need to find the set of all output
values.
In terms of ordered pairs, that correlates with the second component of
each one. In terms of this two dimensional graph, that corresponds with
the y values (vertical axis).
Since that is the case, we need to
look up and
down and see if there are any end points. In this case,
note
how the curve has a low endpoint of y =
-5
and it has arrows at both ends going up, that means it would go up on
and
on forever.
This means that the range is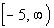 . . |
 Example
2 Example
2: Graph the function 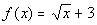 using the given values of x. Also
use
the graph to determine the domain and range of the function. x = 0, 1, 4, 9 |
Step 1: Find at
least four ordered pair solutions. |
I’m going to use a chart to organize my
information. A chart
keeps track of the x values that you are
using
and the corresponding y value found when
you
used a particular x value.
We will use the four values of x that were
given to find corresponding functional values to give us four ordered
pair
solutions.
Keep in mind that the functional value that we find
correlates to the
second or y value of our ordered pair. |
|
x
|
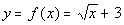
|
(x, y)
|
|
0
|
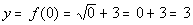
|
(0, 3)
|
|
1
|
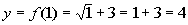
|
(1, 4)
|
|
4
|
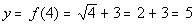
|
(4, 5)
|
|
9
|
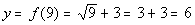
|
(9, 6)
|
Step 2: Plot the
points found in step 1. |
Domain
We need to find the set of all input
values.
In terms of ordered pairs, that correlates with the first component of
each one. In terms of this two dimensional graph, that
corresponds
with the x values (horizontal
axis).
Since that is the case, we need to
look to the
left and right and see if there are any end points. In
this case, note how there is a left
endpoint
at x = 0. Also note that the curve
has
an arrow going to the right, that means it would go on and on
forever
to the right.
This means that the domain
is 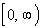 . . |
Range
We need to find the set of all output
values.
In terms of ordered pairs, that correlates with the
second component of each one. In
terms of this
two dimensional graph, that corresponds with the y
values (vertical axis).
Since that is the case, we need to
look up and
down and see if there are any end points. In this case,
note
how the curve has a low endpoint of y =
3 and
it has an arrow going up, that means it would go on and on
forever
up.
This means that the range is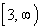 . . |
 Example
3 Example
3: Graph the function 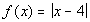 using the given values of x. Also
use
the graph to determine the domain and range of the function. x = 0, 1, 2, 3, 4, 5, 6 |
Step 1: Find at
least four ordered pair solutions. |
I’m going to use a chart to organize my
information. A chart
keeps track of the x values that you are
using
and the corresponding y value found when
you
used a particular x value.
We will use the seven values of x that were
given to find corresponding functional values to give us seven ordered
pair solutions.
Keep in mind that the functional value that we find
correlates to the
second or y value of our ordered pair. |
|
x
|
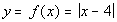
|
(x, y)
|
|
0
|
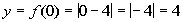
|
(0, 4)
|
|
1
|
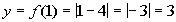
|
(1, 3)
|
|
2
|
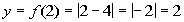
|
(2, 2)
|
|
3
|
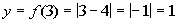
|
(3, 1)
|
|
4
|
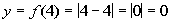
|
(4, 0)
|
|
5
|
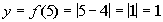
|
(5, 1)
|
|
6
|
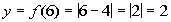
|
(6, 2)
|
Step 2: Plot the
points found in step 1. |
Domain
We need to find the set of all input
values.
In terms of ordered pairs, that correlates with the first component of
each one. In terms of this two dimensional graph, that
corresponds
with the x values (horizontal
axis).
Since that is the case, we need to
look to the
left and right and see if there are any end points. In
this case, note how there are arrows
at both
ends, that means it would go on and on forever to the right and to the
left.
This means that the domain
is 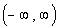 . . |
Range
We need to find the set of all output
values.
In terms of ordered pairs, that correlates with the
second component of each one. In
terms of this
two dimensional graph, that corresponds with the y
values (vertical axis).
Since that is the case, we need to
look up and
down and see if there are any end points. In this case,
note
how the graph has a low endpoint of y = 0
and
it has an arrows that go up, that means it would go up on and on
forever.
This means that the range is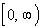 . . |
 Example
4 Example
4: Graph the function 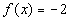 using the given values of x. Also
use
the graph to determine the domain and range of the function. x = -3, -2, -1, 0, 1, 2, 3 |
Step 1: Find at
least four ordered pair solutions. |
I’m going to use a chart to organize my
information. A chart
keeps track of the x values that you are
using
and the corresponding y value found when
you
used a particular x value.
We will use the seven values of x that were
given to find corresponding functional values to give us seven ordered
pair solutions.
Keep in mind that the functional value that we find
correlates to the
second or y value of our ordered pair. |
|
x
|
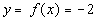
|
(x, y)
|
|
-3
|
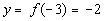
|
(-3, -2)
|
|
-2
|
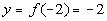
|
(-2, -2)
|
|
-1
|
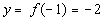
|
(-1, -2)
|
|
0
|
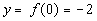
|
(0, -2)
|
|
1
|
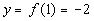
|
(1, -2)
|
|
2
|
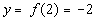
|
(2, -2)
|
|
3
|
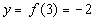
|
(3, -2)
|
Step 2: Plot the
points found in step 1. |
Domain
We need to find the set of all input
values.
In terms of ordered pairs, that correlates with the first component of
each one. In terms of this two dimensional graph, that
corresponds
with the x values (horizontal
axis).
Since that is the case, we need to
look to the
left and right and see if there are any end points. In
this case, note how the curve has
arrows at both
ends, that means it would go on and on forever to the right and to the
left.
This means that the domain
is 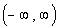 . . |
Range
We need to find the set of all output
values.
In terms of ordered pairs, that correlates with the
second component of each one. In
terms of this
two dimensional graph, that corresponds with the y values (vertical axis).
Since that is the case, we need to
look up and
down and see if there are any end points. In this case,
note
how the line does not go up or down and that all the values of y are -2.
This means that the range is {y | y = -2}. |
 Example
5 Example
5: Graph the function 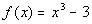 using the given values of x. Also
use
the graph to determine the domain and range of the function. x = -2, -1, 0, 1, 2 |
Step 1: Find at
least four ordered pair solutions. |
I’m going to use a chart to organize my
information. A chart
keeps track of the x values that you are
using
and the corresponding y value found when
you
used a particular x value.
We will use the five values of x that were
given to find corresponding functional values to give us five ordered
pair
solutions.
Keep in mind that the functional value that we find
correlates to the
second or y value of our ordered pair. |
|
x
|
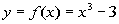
|
(x, y)
|
|
-2
|
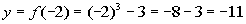
|
(-2, -11)
|
|
-1
|
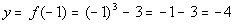
|
(-1, - 4)
|
|
0
|
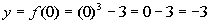
|
(0, -3)
|
|
1
|
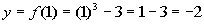
|
(1, -2)
|
|
2
|
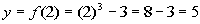
|
(2, 5)
|
Step 2: Plot the
points found in step 1. |
Domain
We need to find the set of all input
values.
In terms of ordered pairs, that correlates with the first component of
each one. In terms of this two dimensional graph, that
corresponds
with the x values (horizontal
axis).
Since that is the case, we need to
look to the
left and right and see if there are any end points. In
this case, note how the curve has
arrows at both
ends, that means it would go on and on forever to the right and to the
left.
This means that the domain
is 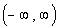 . . |
Range
We need to find the set of all output
values.
In terms of ordered pairs, that correlates with the
second component of each one. In
terms of this
two dimensional graph, that corresponds with the y values (vertical axis).
Since that is the case, we need to
look up and
down and see if there are any end points. In this case, note how the
curve
has arrows at both ends, that means it would go on and on forever up
and
down.
This means that the range is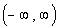 . . |
 Practice Problems Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1e: Graph the given function using
the given values
of x. Also use the graph to determine the domain and
range
of the function. Practice
Problems 1a - 1e: Graph the given function using
the given values
of x. Also use the graph to determine the domain and
range
of the function.
 Need Extra Help on these Topics? Need Extra Help on these Topics?

Last revised on April 7, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.
|
|


