College Algebra
Tutorial 30: Introduction to Functions
 Learning Objectives
After completing this tutorial, you should be able to:
- Know what a relation, function, domain and range are.
- Find the domain and range of a relation.
- Identify if a relation is a function or not.
- Evaluate functional values.
|
Introduction
In this tutorial we will be taking a look at working
with functions.
We will start off by looking for the domain and range. Then, we
will
move on to finding functional values. Don't be thrown by the
different
way function notation looks. When you go to evaluate these
functions,
we are just plugging in values for x and
simplifying,
just like you have done a million times before (it is one of those
types
of problems that I warn students to not make harder than it is).
Just think of finding a functional value as a fancy assignment
statement.
I think we are ready to forge ahead. |
Tutorial
A relation is a set of ordered pairs where the
first components
of the ordered pairs are the input values and the second components are
the output values. |
A function is a relation that assigns to each
input number EXACTLY
ONE output number.
Be careful. Not every
relation is a function.
A function has to fit the above definition to a tee. |
The domain is the set of all input values to which the
rule applies. These are called your independent variables.
These are the values that correspond to the first components of the
ordered
pairs it is associated with. |
The range is the set of all output values. These
are called your dependent variables. These are the values that
correspond
to the second components of the ordered pairs it is associated with. |
 Example
1: Determine if the given relation is function or
not.
Give its domain and range.
{(1, 2), (1, -2), (2, 3), (3, 4)} |
Is this a
function or not?
We need to ask ourselves, does every
first element
(or input) correspond with EXACTLY ONE second element (or
output)?
In this case, the answer is no. The input value of 1 goes with
two
output values, 2 and -2. It only takes one input value to
associate
with more than one output value to be invalid as a function.
So, this relation would not be
an example of
a function.
Domain
We need to find the set of all input values. In terms of ordered
pairs, that correlates with the first component of each one. So,
what do you get for the domain?
If you got {1, 2, 3}, you are correct!
Note that if any value repeats, we only need to list it
one time.
Range
We need to find the set of all output values. In terms of ordered
pairs, that correlates with the second component of each one. So,
what do you get for the range?
If you got {2, -2, 3, 4}, you are absolutely right! |
Example
2: Determine if the given relation is function or
not.
Give its domain and range.
{(5, 10), (10, 10), (15, 10)} |
Is this a
function or not?
We need to ask ourselves, does every
first element
(or input) correspond with EXACTLY ONE second element (or
output)?
In this case, the answer is yes. 5 only goes with 10, 10 only
goes
with 10, and 15 only goes with 10.
Note that a relation can still be
a function if
an output value associates with more than one input value as shown in
this
example. But again, it would be a no no the other way around,
where
an input value corresponds to two or more output values.
So, this relation would be an
example of a
function.
Domain
We need to find the set of all input values. In terms of ordered
pairs, that correlates with the first component of each one. So,
what do you get for the domain?
If you got {5, 10, 15}, you are correct!
Range
We need to find the set of all output values. In terms of ordered
pairs, that correlates with the second component of each one. SO,
what do you get for the range?
If you got {10}, you are absolutely right!
Note that if any value repeats, we only need to list it
one time. |
Example
3: Decide whether y is
a function
of x:  . |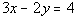
To check if y is a
function of x,
we need to solve for y first and then
check
to see if there is only one output for every input. |
|
*Inverse of add 3x is
sub. 3x
*Inverse of mult. by -2y is div. by -2y
*Solved for y
|
At this point we ask ourselves, would we get one value
for y if you plug in any value for x?
If you answered yes, you are right on. For example, if
we plugged in
a 1 for x, then y would only equal one value, -1/2. Note that ANY value you would
plug
in for x would produce only one value
for y.
Note that since it is solved for y, y is
our output value and x is our input
value.
Since our answer to that question is yes, that means
by definition, y is a function of x. |
Example
4: Decide whether y is
a function
of x:  |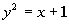
To check if y is a
function of x,
we need to solve for y and then check
to see
if there is only one output for every input. |
|
*Inverse of squaring is taking
the sq. root
*Solved for y |
At this point we ask ourselves, would we get one value
for y if you plug in any value for x?
If you answered no, you are correct.
For example, if our input value x is 3,
then our output value y could either be 2 or -2. Note
that
I could have picked an infinite number of examples like this one.
You only need to show one example where the input value is associated
with
more than one output value to disqualify it from being a function.
This means that at least one input value is
associated with more
than one output value, so by definition, y is not a function of x. |
Function Notation
f(x) read “f of x”
|
f is the function
name. Output
values are also called functional values. Note that you can use any
letter
to represent a function name, f is a very
common
one used.
x is your input
variable.
Think of functional notation as a fancy assignment
statement.
When you need to evaluate the function for a given value of x,
you simply replace x with that given
value
and simplify. For example, if we are looking for f(0),
we would plug in 0 as the value of x in
our
function f. |
Example
5: Find the functional values f(-2), f(0),
and f(1) for the function  . |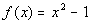
Again, think of functional notation as a fancy
assignment statement.
For example, when we are looking for f(0),
we are going to plug in 0 as the value of x in
our function f and so forth. |
|
*Plug in -2 for x and evaluate
*Plug in 0 for x and evaluate
*Plug in 1 for x and evaluate
|
So our answers are f(-2)
= 3, f(0)
= -1, and f(1) = 0. |
Example
6: Find the functional values g(-5), g(0),
and g(5) for the function  . |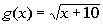
|
*Plug in -5 for x and evaluate
*Plug in 0 for x and evaluate
*Plug in 5 for x and evaluate
|
So our answers are ,  ,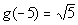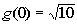
and  . |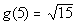
Example
7: Find and simplify a) f( a),
b) f( a + h)
and c)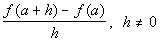 
using the function  . |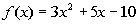
f(a):
Don't let the fact that we need to plug in an a throw you. You plug it into the function just like you do a
number.
Everywhere you have an x in your
function,
replace it with an a. |
f(a + h)
Don't let the fact that we need to plug in the
expression a + h throw you. You plug it into
the function
just like you do a number. Everywhere you have an x in your function, replace it with an a + h. |
|
*Plug in a + h for x and evaluate
|
:
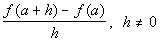Putting it all together we get: |
|
*Plug in f( a + h) and f(a)
found above
*Combine like terms
*Divide out h from
every term
|
|
Constant Function
A function of the form
f(x) = C,
where C is a constant.
|
If the function is constant, that means that the
functional value
never changes, it is always equal to that constant.
Example
8: Find the functional values h(0) and h(2) of the constant function h(x)
= -5. |
Since there is no x to
plug into, the functional
value is going to be -5 no matter what x is. |
A compound function is also known as a piecewise
function.
The rule for specifying it is given by more than one
expression.
Example
9: Find the functional values f(1), f(3),
and f(4) for the compound function |
To find f(1), we
need to go to the
piece of the function that x = 1 would
be under,
which would be the first one where x < 3. |
|
*This piece of the function is
used when x <
3
*Plug in 1 for x |
To find f(3), we
need to go to the
piece of the function that x = 3 would
be under,
which would be the first one where x < 3. |
|
*This piece of the function is
used when x <
3
*Plug in 3 for x |
To find f(4), we
need to go to the
piece of the function that x = 4 would
be under,
which would be the last one where x >
3. |
|
*This piece of the function is
used when x > 3
*Plug in 4 for x
|
|
Finding the Domain
Given an Equation
|
As mentioned above, the domain is the set of all input
values to which
the rule applies. If you are needing to find the domain given an
equation, you want to look for all values of x that would give you a real number answer for your functional
value.
A way to approach this is to look to see if there are any
restrictions.
If there are none, your domain is all real numbers. But,
sometimes
that is not the case. For example, if your function has a
denominator,
you have to be careful that the denominator does not equal 0. You
would have to restrict values for x that
would
cause the denominator to be 0. Or if you had a square root as
part
of your function, you would have to be careful to not include values of x that would cause the expression under the square root to be
negative.
Let's look at a couple examples to illustrate what I'm talking about
here. |
Example
10: Give the domain of the function  . |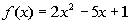
Since we can plug in any value for x (input
variable) and get a real number answer for our function (output
variable),
then there are no restrictions. Therefore the domain is all
real
numbers. |
Example
11: Give the domain of the function  . |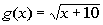
This time we do have a restriction on our domain.
We can only
take the square root of a number greater than or equal to 0. So we must
set the radicand (the inside of the radical) greater than or equal to 0. |
|
*Inv. of add. 10 is sub. 10
*This is our domain
|
Only values of x that
are greater than
or equal to -10 make the original radicand greater than or equal to 0, so
x>-10 is our domain for this
function. |
Example
12: Give the domain of the function  . |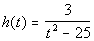
Our restriction here is that the denominator of a
fraction can never
be equal to 0. So to find our domain, we want to set the
denominator
equal to 0 and restrict those values. |
|
*The den. cannot equal to 0
*Factoring to help "solve"
*5 and -5 are restricted values |
Our domain would be all real numbers except 5 and -5,
because
5 and -5 both make the denominator equal 0, which would not give us a
real
number answer for our function. |
Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1b: Determine if the given relation
is function or
not. Give its domain and range.
Practice
Problems 2a - 2b: Decide whether y is a
function of x.
Practice
Problem 3a: Find f(-5) and f(2)
for the given
function.
Practice
Problem 4a: Find and simplify a) f(a),
b) f(a + h) and 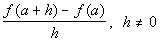using the given function.
Practice
Problem 5a: Find the functional values g(-1), g(0),
and g(4) for the compound function.
Practice
Problems 6a - 6c: Give the domain of the function.
Need Extra Help on these Topics?
Last revised on March 30, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.
|
|
