College Algebra
Tutorial 28: Parallel and Perpendicular Lines
 Learning Objectives Learning Objectives
After completing this tutorial, you should be able to:
- Find the slope of a line that is parallel to a given
line.
- Find the slope of a line that is perpendicular to a
given line.
|
 Introduction Introduction
This tutorial looks at the relationship between the
slopes of parallel
lines as well as perpendicular lines. Once again we are going to
be using material from our math past to help find the new
concept.
You will need to know how to find the slope of a line given an equation
and how to write the equation of a line. If you need a review on
these concepts, feel free to go to Tutorial
26: Equations of Lines. Let's see what you
can
do with parallel and perpendicular. |
 Tutorial Tutorial
Parallel Lines and Their Slopes
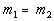
|
In other words, the slopes of parallel lines are
equal.
Note that two lines are
parallel if their slopes
are equal and they have different y-intercepts.
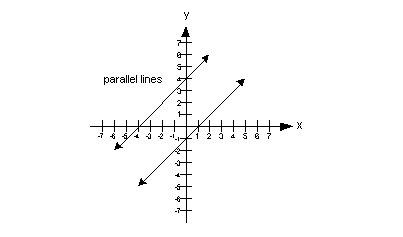
|
Perpendicular Lines and Their
Slopes
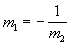
|
In other words, perpendicular
slopes are negative
reciprocals of each other.
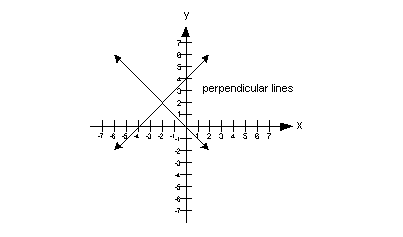
|
Here is a quick review of the slope/intercept form of a
line.
If you need more of a review on how to use this form, feel free to go
to Tutorial
26: Equations of Lines. |
|
Slope/Intercept Equation of a
Line
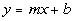
|
If your linear equation is written in this form, m represents the slope and b represents
the y-intercept.
This form can be handy if you need to find the slope of
a line given
the equation. |
 Example
1 Example
1: Find the slope of any line that is a)
parallel
and b) perpendicular to the line 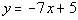 . |
Before we tackle finding the parallel and perpendicular
slopes it really
can help us out if we find the slope of the given line.
Recall that when you are given the equation of a line
that you can find
the slope of it by writing it in the slope/intercept
form, 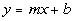 ,
where m is the slope and b is
the y-intercept of the line. ,
where m is the slope and b is
the y-intercept of the line.
This equation is already written in the
slope/intercept form: |
|
*Written in slope/intercept
form |
Lining up the form with the equation we have been
given, can
you see what the slope is?
If you said -7, you are correct!!!
Slope of the parallel line:
Since parallel lines have the same slope what do you think the slope
of any parallel line to this line is going to be? Pat yourself on the
back if you
said
-7.
Slope of the perpendicular line:
Since the slopes of perpendicular lines are negative reciprocals of
each other, what do you think the slope of any perpendicular line
to this line is?
Give yourself a high five if you said 1/7.
Remember that you take the reciprocal which is -1/7 and
then you negate
it to get the 1/7 for your perpendicular slope.
The slope of any parallel line to the line 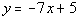 is -7 and the slope of any perpendicular
line to the line is -7 and the slope of any perpendicular
line to the line 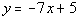 is 1/7. is 1/7. |
 Example
2 Example
2: Find the slope of the line that is a)
parallel
and b) perpendicular to the line 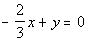 . |
Before we tackle finding the parallel and perpendicular
slopes it really
can help us out if we find the slope of the given line.
Recall that when you are given the equation of a line
that you can find
the slope of it by writing it in the slope/intercept
form, 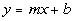 ,
where m is the slope and b is
the y-intercept of the line. ,
where m is the slope and b is
the y-intercept of the line.
Rewriting this equation in the slope/intercept form
we get: |
|
*Inverse of sub. 2/3x is add. 2/3x
*Written in slope/intercept form
|
Lining up the form with the equation we got, can
you see what the
slope is?
If you said 2/3, you are correct!!!
Slope of the parallel line:
Since parallel lines have the same slope what do you think the slope
of the parallel line is going to be? Pat yourself on the back if you
said
2/3.
Slope of the perpendicular line:
Since the slopes of perpendicular lines are negative reciprocals of
each other, what do you think the slope of the perpendicular line
is?
Give yourself a high five if you said -3/2.
Remember that you take the reciprocal which is 3/2 and
then you negate
it to get the -3/2 for your perpendicular slope.
The slope of the parallel line is 2/3 and the slope
of the perpendicular
line is -3/2. |
 Example
3 Example
3: Find the slope of the line that is a)
parallel
and b) perpendicular to the line 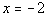 . |
Do you remember what special type of line this equation
is? It
is a vertical line. If you need a review on vertical lines, feel
free to go to Tutorial
27: Graphing Lines.
What is the slope of a vertical line? If
you said undefined,
you are right on.
Slope of the parallel line:
Since parallel lines have the same slope, what do you think the slope
of the parallel line is going to be? Pat yourself on the back if you
said
undefined.
Slope of the perpendicular line:
Since slopes of perpendicular lines are negative reciprocals of each
other, what do you think the slope of the perpendicular line is?
This one is a little trickier. Vertical lines and horizontal
lines
are perpendicular to each other. The slope of the perpendicular
line
in this case would be the slope of a horizontal line which would be
0.
The slope of the parallel line is undefined and the
slope of the
perpendicular line is 0. |
 Example
4 Example
4: Find the slope of the line that is a)
parallel
and b) perpendicular to the line 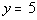 . |
Do you remember what special type of line this equation
is? It
is a horizontal line. If you need a review on horizontal lines,
feel
free to go to Tutorial
27: Graphing Lines.
What is the slope of a horizontal line? If
you said 0,
you are right on.
Slope of the parallel line:
Since parallel lines have the same slope, what do you think the slope
of the parallel line is going to be? Pat yourself on the back if you
said
0.
Slope of the perpendicular line:
Since slopes of perpendicular lines are negative reciprocals of each
other, what do you think the slope of the perpendicular line is?
This one is a little trickier. Vertical lines and horizontal
lines
are perpendicular to each other. The slope of the perpendicular
line
in this case would be the slope of a vertical line which would be
undefined.
The slope of the parallel line is 0 and the slope of
the perpendicular
line is undefined. |
Here is a quick review of the point/slope form of a
line. If
you need more of a review on how to use this form, feel free to go to Tutorial
26: Equations of Lines |
|
Point/Slope Form of an Equation
A line going through the point 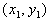 and and
having slope of m would have the equation
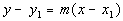
|
We can use this form to plug into when we need to
come up with a
linear equation.
When writing an equation of a line, keep in mind that you
ALWAYS need two pieces of information when you go to write an equation:
- ANY point on the line
- Slope
Once you have these two pieces of
information,
you plug the x and y values from your point and the slope (m)
value
into the point/slope formula. |
 Example
5: Example
5: Write an equation for the line in point/slope form
and slope/intercept form that passes through (-2, -5) and parallel to
the
line 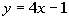 . |
What are the two things we need to write an equation
of a line????
If you said any point on the line and the slope, you are
correct.
We have a point, however what about the slope?
Does this mean
we can’t work out the problem? You are not going to get off that
easily.
We need to do a little digging to get our slope.
As mentioned above, parallel
lines have the same
slope. So, if we know the slope of the line parallel to
our
line, we have it made.
Let’s find the slope of the
given line: |
|
*Slope/intercept form of the
line |
Now keep in mind that this is not the equation of our
line but of a
line parallel to our line. We needed to write it this way so we
could
get the slope. And it looks like the slope is 4. Since our
line is parallel to a line that has a slope of 4, our line also has
a slope of 4.
OK, now we have our slope, which is 4. Now it is
just like problems
in Tutorial 26: Equations of
Lines,
we put the slope and one point into the point/slope equation.
Point/Slope Form: |
|
*Point/slope form of the line
|
Make sure that you are careful when one of your
values is negative
and you have to subtract it as we did in line 2. y - (-5) is not he same as y - 5
and x - (-2) is not the same
as x - 2. |
Next, we want to write it in the Slope/Intercept
Form, which basically means we need to solve for y: |
|
*Dist. the 4 through ( )
*Inverse of add. 5 is sub. 5
*Slope/intercept form of the
line |
The equation of the line that passes through (-2,
-5) and is parallel
to the line 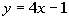 is
y + 5 = 4(x + 2) OR y = 4x + 3. is
y + 5 = 4(x + 2) OR y = 4x + 3. |
 Example
6: Example
6: Write an equation for the line in point/slope form
and slope/intercept form that passes through (3, 2) and perpendicular
to
the line 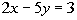 . |
What are the two things we need to write an equation
of a line????
If you said any point on the line and the slope, you are
correct.
We have a point, however what about the slope?
Does this mean
we can’t work out the problem? You are not going to get off that
easily.
We need to do a little digging to get our slope.
As mentioned above, the slopes
of perpendicular
lines are negative reciprocals of each other. So, if we
know
the slope of a line perpendicular to our line, we have it made.
Let’s find the slope of the
given line: |
|
*Inverse of add. 2x is sub. 2x
*Inverse of mult. by -5 is div.
by -5
*Slope/intercept form of the
line
|
Now keep in mind that this is not the equation of our
line but of the
line parallel to our line. We needed to write it this way so we
could
get the slope. And it looks like the slope is 2/5. Since
our
line is perpendicular to a line that has a slope of 2/5, our line
has
a slope of -5/2 (the negative reciprocal of 2/5).
OK, now we have our slope, which is -5/2. Now it
is just like
problems in Tutorial 26:
Equations
of Lines, we put the slope and one point into the point/slope
equation.
Point/Slope Form: |
|
*Point/slope form of the line
|
Next, we want to write it in the Slope/Intercept
Form, which basically means we need to solve for y: |
|
*Dist. the -5/2 through
( )
*Inverse of sub. 2 is add. 2
*Slope/intercept form of the
line
|
The equation of the line that passes through (3, 2)
and perpendicular
to the line 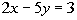 is y - 2 = -5/2(x - 3) OR y = -5/2x + 19/2. is y - 2 = -5/2(x - 3) OR y = -5/2x + 19/2. |
 Practice Problems Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1c: Find the slope of the line that
is a) parallel
and b) perpendicular to the given line. Practice
Problems 1a - 1c: Find the slope of the line that
is a) parallel
and b) perpendicular to the given line.
 Practice
Problems 2a - 2b: Write an equation for the line
in point/slope
form and slope/intercept form that has the given condition. Practice
Problems 2a - 2b: Write an equation for the line
in point/slope
form and slope/intercept form that has the given condition.
 Need Extra Help on these Topics? Need Extra Help on these Topics?

Last revised on Feb. 20, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.
|
|


