GRE Math Practice Test I
Answer Key with Explanantions
WTAMU > Virtual Math Lab > GRE Math
| This page contains the answers to Practice Test I with detailed explanations. |
Column A
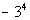 |
Column B
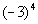 |
 Answer:
B Answer:
B

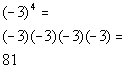
Hey, they look a lot alike, but they are not exactly the
same.
Can you see the difference between the two?? Hopefully, you noticed
that in Column B, there was a ( ) around the - and the 3. In Column A, there
is no ( ). This means the - is NOT part of the base, so it will
not get expanded like it did in Column B. It is interpreted as
finding the negative or opposite of 3 to the fourth power.
Hence, Column B's value is greater than Column A's value.
Need more help on this topic? Exponents
|
2. x
and y are integers: 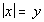 |
 Answer:
D Answer:
D
The reason that the answer is D on this
problem is that opposites have the same absolute value. Since x
and y are integers, x
could be a positive or negative value or zero. Since y
is set equal to the absolute value of x,
then y’s
value will always be nonnegative. Based on the information
given, x could be a negative value, and
in that case, y would always be
greater.
But if x is a nonnegative value, then x
and y will be the same value. For example, x
could be -5, then y = 5. But x
could be 5, where y = 5.
So, the relationship cannot be
determined from the information given.
Need more help on this topic? Absolute
Value
|
Column A
.25% of .25 |
Column B
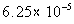 |
 Answer:
A Answer:
A
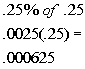
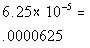
|
*Move decimal on .25% two places to
the left
*Move decimal 5 places to the LEFT
|
4. If 25 students in one class had an average
of 93% and 20 students from another class had an average of 98%, approximately
what is the average in percent of all 45 students? |
 Answer: D
Answer: D
In general, when finding the average of tests, you add the
tests together and then divide by the number of tests. On this problem we have
two separate averages to start with. So we need to find the total number of
points we have using that information and then divide by the number of
students, which in this case is 45.
If 25 students averaged 93, then the total number of points
would be (25)(93) = 2325.
If 20 students averaged 98, then the total number of points
would be (20)(98) = 1960.
So the total number of points is 2325 + 1960 = 4285.
To find the average, take the number of points and divide
by the number of students:
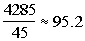
The overall average percent is 95.2%.
Need more help on this topic? Averages
(Mean) |
5. A water treatment plant is built with two
cylindrical tanks to contain water for a town. Each tank has a radius of 10
feet and a depth of 20 feet. If there are about 7.5 gallons in a cubic
foot of water, approximately how many gallons of water can be treated
at the plant at any one time? |
 Answer: C Answer: C
First, let’s find the volume of each cylindrical tank. The
volume of a cylindrical tank is
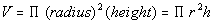
Filling in 10 for radius and 20 for height we get:
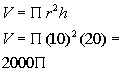
Next we want to consider the fact that we have two tanks. Multiplying
the volume by two we get:
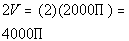
Next we want to consider that there are about 7.5 gallons in a
cubic foot of water. Multiplying the volume of the two cylinders by
7.5 we get:
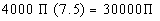
Next notice that none of the answers has the pi symbol in
them. That means we will have to put in 3.14 for pi
and see what we get:
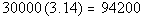
94,200 gallons of water can be treated at the water plant
at one time.
Need more help on this topic? Formulas
for Three-Dimensional Figures
|
Column A
Probability of randomly selecting
a given name out of a hat
containing 12 different names. |
Column B
.08
|
 Answer:
A Answer:
A
In Column A, each name has an equally likely chance of being
picked.
The probability of randomly selecting a given name out if a
hat containing 12 different names can be found by taking the number of names being
selected, which in this case is 1, and put that over the total number of names,
which is 12:

Since .08333... is larger than .08, then the probability of
randomly selecting a given name out if a hat containing 12 different names is a
larger value than .08.
Need more help on this topic? Probability
|
7. If 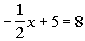
what is the value of 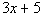 ? |
 Answer: A Answer: A
The first step here is to find the value of x.
If we know that, then we can plug that in to the second expression and
find out what 3x + 5 is.
Solving the equation for x
we get:
|
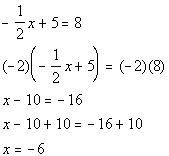 |
*Mult. BOTH sides by the LCD of -2
*Inverse of sub. 10 is add 10 to BOTH
sides
|
Now be careful, this is not our final answer.
We still need to plug in -6 for x
in the given expression:
|
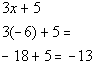 |
*Plug in -6 for x
|
8. x is a
positive integer: 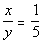 |
 Answer:
D Answer:
D
If we did a cross multiplication we would get:
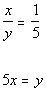
It is given that x is a
positive integer.
That could mean x is 1, 2, 3, ....
If x is 1, then y would equal 5. However, if x is an
integer greater than or equal to 2 then y would
be greater than 5. Since we don’t know x’s
exact value, then we cannot determine the relationship between 5 and y.
Need more help on this topic? Solving
Linear Equations
|
Column A
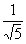 |
Column B
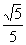 |
 Answer: C Answer: C
Rationalizing the denominator in Column A we get:
|
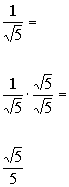 |
*Mult. num. and den. by square root of 5
|
The two quantities are equal to each other.
Need more help on this topic? Square
Root
|
10.

What is the area of the rectangle above?
|
 Answer: E Answer: E
The area of a rectangle is length times width. So, we
need the length and the width to get our answer.
It looks like we have the length which is 10, but we still
need the width.
Note how we have the diagonal of the rectangle which is
12. The diagonal, length and width of the rectangle make up an right
triangle. Anytime you are missing one side of a right triangle, you can use the
Pythagorean theorem to find that long lost side.
Using the Pythagorean Theorem we get:
|
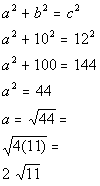 |
*Pythagorean Theorem
*Plugging in 10 for one leg and 12
for the hypotenuse
*Subtract 100 form BOTH sides
*Take the square root of BOTH sides
*Square root of 4 is 2
|
2 square root of 11 is the width of the rectangle.
Putting the length and the width values of the rectangle
into the area formula we get:
|
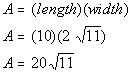 |
*Plugging in 10 for length and 2 sq.root
of 11 for width
|
Column A
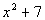 |
Column B
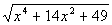 |
 Answer: C Answer: C |
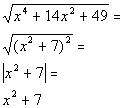 |
*Factor the Perfect Square Trinomial
*The sq. root of an expression
squared is the abs. value of that expression
*Since x
squared plus 7 is ALWAYS positive it is equal to its abs. value
|
12. What is the area of a circle that is
inscribed in a square whose area is 81 square inches? |
 Answer: D Answer: D
Ultimately, we need to find the area of the circle. That
means we need the area of a circle formula which is

Since we were not given the radius of the circle, it looks
like we will have to go out and find it.
Since the area of a square is found by taking the side
squared, this means the side of our square is going to be 9 inches, since its area is
81 square inches.
Let's look at a visual of this:
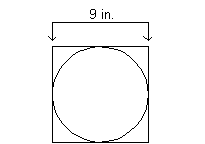
It looks like the side of the square is also the diameter of
the circle. Since the diameter is 9, the radius, which is half of the diameter, is
going to be 9/2 or 4.5.
Putting the radius into the area formula we get:
|
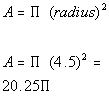 |
*Plugging in 4.5 for the radius
|
13. Being a conscientious driver, Suzy stayed
at or below the speed limit while traveling down the interstate. Overall, she
went an average rate of 65 mph and it took her 10 hours to complete her
journey. If she traveled for 6 of her 10 hours at 70 mph, what
constant speed did she go for the remaining 4 hours to obtain the overall 65 mph
average? |
 Answer: C Answer: C
This problem has several parts to it. We
will need to use the formula distance = (rate)(time) to help us out with
this.
First let see how many miles Suzy
traveled overall.
Plugging in the rate of 65 mph and the time of 10 hours we get:
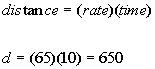
Suzy traveled a total of 650 miles.
Next we start breaking it down. It
says that she traveled for 6 hours at 70 mph. From this we can
figure out how many of the 650 miles she traveled at this speed:
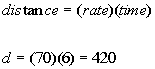
She traveled 420 miles at the 70
mph.
How many miles does that leave us for
the unknown speed?
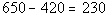
For the last part, we are again going to
use the distance/rate formula, but now we are looking for the rate. Plugging
in 230 for the distance and 4 for the time we get:
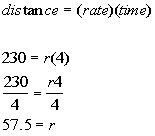
Suzy traveled 57.5 mph for 4 hours of her trip.
Need more help on this topic?
Word Problems
|
14. 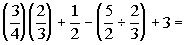 |
 Answer:
C Answer:
C |
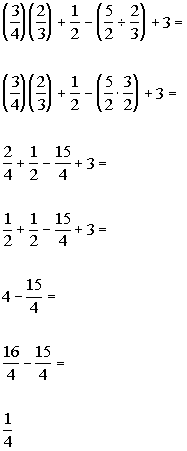 |
*Change the division to mult. of the recip.
*Find the products
|
15.

Find the area of the graph above enclosed by figure ABCD.
|
 Answer:
B Answer:
B
From the picture, we can see that figure ABCD is a
quadrilateral but doesn’t fit into a form like rectangle, parallelogram, etc... We
will have to take the area of triangle ABE and subtract from it the
area of triangle CDE, this will leave us with figure ABCD.
Lets look at triangle ABE first. The area of a triangle
is ½
(base)(height). So we need to know the base and the height of
this triangle. Since it is a right triangle, the base and height are
going to be the lengths of the two legs, which are sides AB and AE.
Side AB can be found by taking the absolute value of the
difference of the y values of their ordered pairs,
which would be 12 - 0 = 12.
Side AE can be found by taking the absolute value of the
difference of the x values of their ordered pairs,
which would be 6 - 0 = 6.
Plugging 6 in for the base and 12 in for the height into
the formula for the area of a triangle we get:
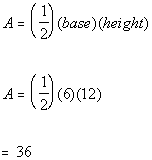
The area of triangle ABE is 36.
Now lets look at triangle CDE. The area of a triangle is
½
(base)(height). So we need to know the base and the height of
this triangle. The base of this triangle is side DE. The height can be
found by making a perpendicular line from C to the base.
Side DE can be found by taking the absolute value of the
difference of the x values of their ordered pairs,
which would be 6 - 3 = 3.
The height can be found by taking the absolute value of the
difference of the y value of C and 0 (the y
value on the base), which would be 4 - 0 = 4.
Plugging 3 in for the base and 4 in for the height into the
formula for the area of a triangle we get:
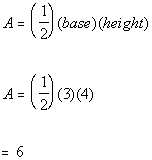
The area of triangle CDE is 6.
Last, we need to take the difference of the areas of the
two triangles:
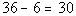
The area of the figure ABCD is 30.
Need more help on these topics? Formulas
for Two-Dimensional Figures and Coordinate
Geometry
|
16. 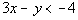 |
Column A
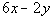 |
Column B
-10 |
 Answer: D Answer: D
Note how 6x - 2y
is two times 3x - y.
Taking 2 times the given inequality we get:
|
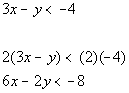 |
*Taking 2 times BOTH sides |
It looks like 6x - 2y is less than -8. 6x - 2y
could be -8.5 or it can be -12, in other words 6x
- 2y can be either less than or greater
than -10.
Since this is our only given information, the relationship
cannot be determined from the given information.
Need more help on this topic? Linear
Inequality
|
17. If account codes for a certain company are
assigned as follows: two letters and then three one digit numbers, how many
different account codes can be made? Note that letters and digits can be
repeated. |
 Answer:
B Answer:
B
We can use the fundamental counting principle to answer this
question.
Basically we need to take the product of the number of ways each event
can occur.
There are 5 stages or events: letter 1,
letter 2, digit 1, digit 2, and digit 3.
In general, there are 26 letters in the alphabet.
Neither letter has any restriction, so there are 26 possibilities for each
letter.
In general there are 10 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and
9.
There are no restriction on any of the digits, so each one of those has
10 possibilities.
Putting that all together we get:
|
|
Letter 1
|
|
Letter 2
|
|
Digit 1
|
|
Digit 2
|
|
Digit 3
|
|
Total
|
|
26
|
x
|
26
|
x
|
10
|
x
|
10
|
x
|
10
|
=
|
676000
|
There are 676,000 different account codes possible.
Need more help on this topic? Counting
Principle
|
18.

In the figure above, XY is a
line segment.
What is the value of  ? ?
Note that a and b are measured in degrees.
|
 Answer: D Answer: D
Since 4 angles of measure a
make up XY
and XY is a line segment that
means, the 4 a angles would have to make up 180
degrees.
Similarly, the 3 b angles would
be 180 degrees.
This would give us enough information to find out what a and b are equal to.
Lets start with a:
|
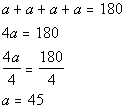 |
*The 4 a
angles = 180 degrees
*Divide BOTH sides by 4
|
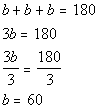 |
*The 3 b
angles = 180 degrees
*Divide BOTH sides by 3
|
Putting those values in for a
and b we get: |
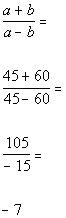 |
*Plug in 45 for a
and 60 for b
|
19. 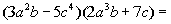 |
 Answer:
B Answer:
B |
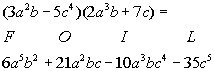 |
*Use the FOIL method to mult. two
binomials
*Make sure you add exponents when you
mult. like bases
|
20.
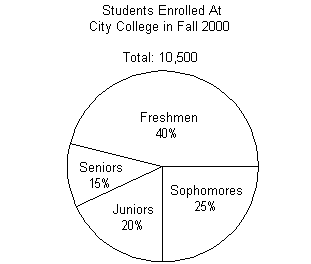 |
Column A
The ratio of juniors to seniors at
City College in the
Fall 2000 semester. |
Column B
The ratio of seniors to juniors at
City College in the
Fall 2000 semester. |
 Answer:
A Answer:
A
You can do this problem two different ways. You can
either take the ratio of the percents for each classification or you can find the
number of students that go with each one and take that ratio. Either way
you would end up with the same answer.
I’m going to use the percents that are given to set up each
ratio.
For the ratio of juniors to seniors at City College in
the Fall 2000 semester, we need to make sure that the percent attached to
juniors goes on top and the percent for seniors goes on bottom:
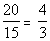
For the ratio of seniors to juniors at City College in
the Fall 2000 semester, we need to make sure that the percent attached to
seniors goes on top and the percent for juniors goes on bottom:
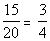
It looks like the ratio of juniors to seniors is greater
than the ratio of seniors to juniors.
Need more help on this topic? Percent
and Problem Solving
|
21.

If enrollment was 17% higher for freshmen at City College in
the Fall 2000 semester than the Fall 1999 semester, approximately what was the
enrollment of freshman in the Fall 1999 semester?
|
 Answer: A Answer: A
We need to be careful here, the temptation is to just take 40%
- 17% = 23% of the enrollment of 10,500. However, keep in mind
that we are talking about 17% higher in terms of enrollment, not compared to
the other classifications and enrollment may or may not have been the
same overall for 1999 and 2000.
The first thing we need to find is the actual enrollment for
freshmen in 2000. According to the chart, freshmen made up 40% of the
10,500 enrolled. Taking 40% of 10,500 we get:
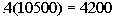
4200 is 17% higher than the enrollment of freshmen in
1999. Letting x
represent the 1999 freshmen enrollment and putting this into an
equation we get:
|
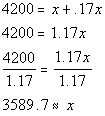 |
*17% higher means we ADD 17% (or
.17) of the amount
*Divide BOTH sides by 1.17
|
22.

If the areas of sectors in the circle graphs are drawn in
proportion to the percentages shown, what is the measure, in degrees, of the
central angle sector representing the percentage of juniors enrolled in the
Fall 2000 semester?
|
 Answer: D Answer: D
On this problem, the key is to know that a circle measures 360
degrees. So if we know the percentage of the circle that a sector represents,
then we can take that percentage of 360 degrees and find the measure of just
that sector.
Since juniors were 20% of the enrollment, we need to take
20% of 360:
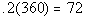
The measurement of the central angle sector representing
the percentage of juniors enrolled in the Fall 2000 semester is 72 degrees.
Need more help on this topic? Percent
and Problem Solving
|
Column A
Mode of the numbers listed |
Column B
Standard deviation of the numbers listed |
 Answer: A Answer: A
The mode of a set of data is the value(s) that occurs most
often. In this case, all three values occur twice. So the mode is 3,
4, and 5.
For the standard deviation, we need to first find the mean:
|
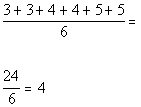 |
*(sum of values)/(number of values)
|
The mean of these values is 4.
Next we need to find the difference between the mean and each
separate value of the data set,
AND square each difference found AND add up all of the squared
values found:
|
|
x
|
x - 4
|

|
|
3
|
-1
|
1
|
|
3
|
-1
|
1
|
|
4
|
0
|
0
|
|
4
|
0
|
0
|
|
5
|
1
|
1
|
|
5
|
1
|
1
|
| |
SUM:
|
4
|
Next we need to divide the sum found by the number of data
values in the set AND find the nonnegative square root of the quotient found.
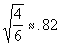
On the test you will not have a calculator, so on a problem
like this you need to estimate. You can see that you are taking the square
root of a number that is between 0 and 1, so your answer will be between 0 and 1.
This means that the mode, whether it is 3, 4, or 5, is always greater
than the standard deviation.
Need more help on this topic? Central
Tendencies
|
24.

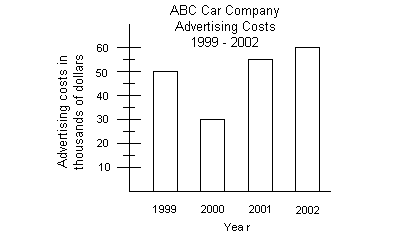
What is the mean of the advertising costs from 1999 to
2002?
|
 Answer: A Answer: A
Since we are looking for the mean of advertising costs, we
need to look at the 2nd bar graph.
Keep in mind that the advertising costs are in thousands of
dollars. In 1999, the advertising cost is $50000, in 2000 it is $30000, in 2001
it is $55000, and in 2002 it is $60000.
To find the mean we need to sum up all the values and then
divide by the number of values.
|
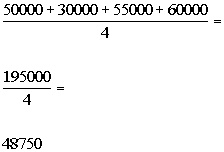 |
*(sum of values)/(number of values)
|
25.


The percent decrease in profits from 1999 to 2000 was
approximately what percent?
|
 Answer:
C Answer:
C
Since we are looking at the decrease in profits, we need to
look at the 1st bar graph.
1999 had a profit of $250,000,000 and 2000 had a profit of
$150,000,000.
We are needing to find the percent decrease in profits from
1999 to 2000. First lets see what the decrease in dollar amount was:
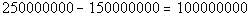
There was a $100,000,000 decrease in profits from 1999 to
2000. From this we need to find out what percent 100,000,000 is of
250,000,000, since that is the amount we are decreasing from:
|
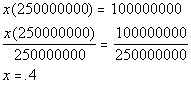 |
*x
represents the percent we are looking for
|
26.

Looking at the figure above, if triangle ABC is an equilateral
triangle and line BC is parallel to line DE, what is the measure of angle
5?
|
 Answer: C Answer: C
Lets see what the information that was given to us
means. If ABC is an equilateral triangle, that means all three sides are equal and
all three angles have the same measurement. That means, angles 1, 2,
and 3 are each 60 degrees. The reason for that is the degrees of
all three angles of any triangle sum up to be 180 degrees. If all
three angels are the same, then they would each have to be 60 degrees,
because 60 + 60 + 60 = 180.
Now we have a value to work with.
We have to work our way to angle 5.
Next, we can use the fact that lines BC and DE are parallel to
each other and ray AE is a transversal that intersects these two
lines. This means angles 3 and 4 are equal to each other because they are
corresponding angles. So this means angle 4 is also 60 degrees.
We are getting closer.
Note how angles 4 and 5 together make a straight angle.
This means their sum is 180 degrees. Well if angle 4 is 60 degrees, this
means angle 5 must equal 180 - 60 = 120 degrees.
Angle 5 is 120 degrees.
Need more help on this topic? Basic
Geometry
|
27.
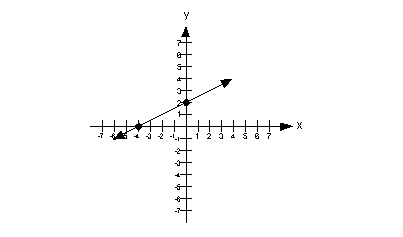 |
Column A
Slope of the line on graph above. |
Column B
The y value of the y-intercept
of the line on the graph above. |
 Answer: B Answer: B
The slope can be found by using rise/run. I prefer to go
left to right. I’m going to start with the point that is on the x-axis,
which is (-4, 0) and then step up to the point that is on the y-axis
(0, 2). If we do that, we rise up 2 and go over to the right 4.
So the slope is rise/run which is 2/4 = 1/2.
The y-intercept is the point
where the graph crosses the y-axis. In this case
that is (0, 2). The y-value of that
point is 2.
This means the y value of
the y-intercept of the graph is greater than the slope of the line.
Need more help on this topic? Coordinate
Geometry
|
28. What is the solution(s) to 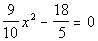 ? |
 Answer: B Answer: B |
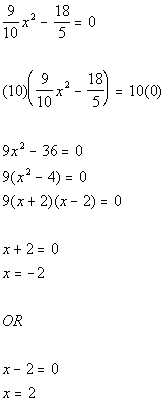 |
*Multiply BOTH sides by the LCD 10
*Factor out a GCF of 9
*Factor the difference of squares
*Set 1st factor = 0
*Set 2nd factor = 0
|

WTAMU > Virtual Math Lab > GRE Math
Disclaimer:
Note that we can not
guarantee that you will pass your test after going through any of the tutorials
in this website. However, it will definitely help you to better
understand the topics covered. WTAMU and Kim Seward are not responsible
for how a student does on any test for any reason including not being able
to access the website due to any technology problems.
GRE and Graduate Record Examination are the
registered trademarks of Educational Testing Service (ETS). The material here has
neither been reviewed nor endorsed by ETS.
Throughout this website, we link to various
outside sources.
WTAMU and Kim Seward do not have any ownership to any of these outside
websites and cannot give you permission to make any kind of copies of
anything found at any of these websites that we link to. It is purely for
you to link to for information or fun as you go through the study
session. Each of these websites have a copy right clause that you need to read
carefully if you are wanting to do anything other than go to the website and read
it. We discourage any illegal use of the webpages found at these
sites.
|
All contents copyright (C) 2003 - 2008, WTAMU and Kim Seward. All rights reserved.
Last revised on September 29, 2008 by Kim Seward.
|
|
|


