College Algebra
Tutorial 6: Polynomials
 Learning Objectives Learning Objectives
After completing this tutorial, you should be able to:
- Identify a term, coefficient, constant term, and polynomial.
- Tell the difference between a monomial, binomial, and trinomial.
- Find the degree of a term and polynomial.
- Combine like terms.
- Add and subtract polynomials.
- Multiply any polynomial times any other polynomial.
- Use the FOIL method to multiply a binomial times a binomial.
- Use special product rules to multiply a binomial squared and a product
of a sum and difference of two terms.
|
 Introduction Introduction
In this tutorial we will be looking at the different
components of
polynomials. Then we will move on to adding, subtracting and
multiplying
them. Some of these concepts are based on ideas that were covered
in earlier tutorials. A lot of times in math you use previous
knowledge
to learn new concepts. The trick is to not reinvent the wheel
each
time but recognize what you have done before and draw on that knowledge
to help you work through the problems. |
 Tutorial Tutorial
Let’s start with defining some words before we get to
our polynomial. |
A term is a number, variable or the product of a
number and variable(s).
Examples of terms are 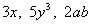 ,
z. ,
z. |
A coefficient is the numeric factor of your
term.
Here are the coefficients of the terms listed above:
|
Term
|
Coefficient
|
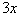
|
3
|
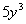
|
5
|
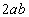
|
2
|
|
z
|
1
|
|
A constant term is a term that contains only a number.
In other
words, there is no variable in a constant term.
Examples of constant terms are 4, 100, and -5. |
|
Standard Form of a
Polynomial
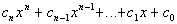
where n is a non-negative
integer.
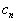 is
called the leading coefficient. is
called the leading coefficient.
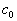 is
a constant. is
a constant.
|
In other words, a polynomial is a finite sum of
terms where the
exponents on the variables are non-negative integers. Note
that
the terms are separated by +'s and -'s. An example of a polynomial expression is 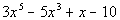 . . |
The degree of a term is the sum of the exponents on
the variables
contained in the term.
For example, the degree of the term 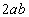 would be 1 + 1 = 2. The exponent on a is
1 and on b is 1 and the sum of the
exponents
is 2. would be 1 + 1 = 2. The exponent on a is
1 and on b is 1 and the sum of the
exponents
is 2.
The degree of the term 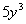 would be 3 since the only variable exponent that we have is 3. would be 3 since the only variable exponent that we have is 3. |
The degree of the polynomial is the largest degree
of all its terms. |
Note that the standard form of a polynomial that is
shown above is
written in descending order. This means that the term that
has
the highest degree is written first, the term with the next highest
degree
is written next, and so forth.
Also note that a polynomial can be “missing”
terms. For example,
the polynomial written above starts with a degree of 5, but notice
there
is not a term that has an exponent of 4. That means the
coefficient
on it is 0, so we do not write it. |
|
Some Types of Polynomials
|
|
Type
|
Definition
|
Example
|
|
Monomial
|
A polynomial with one term
|
5x
|
|
Binomial
|
A polynomial with two terms
|
5x - 10
|
|
Trinomial
|
A polynomial with three terms
|
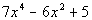
|
 Example
1: Find the degree of the polynomial and
indicate
whether the polynomial is a monomial, binomial, trinomial, or none of
these: Example
1: Find the degree of the polynomial and
indicate
whether the polynomial is a monomial, binomial, trinomial, or none of
these: 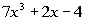 . .
 View a video of this example View a video of this example
|
Since the degree of the polynomial is the highest
degree of all the
terms, it looks like the degree is 3.
Since there are three terms, this is a trinomial. |
 Example
2: Find the degree of the polynomial and
indicate
whether the polynomial is a monomial, binomial, trinomial, or none of
these: Example
2: Find the degree of the polynomial and
indicate
whether the polynomial is a monomial, binomial, trinomial, or none of
these: 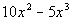 . .
 View a video of this example View a video of this example
|
Since the degree of the polynomial is the highest
degree of all the
terms, it looks like the degree is 3.
Make sure that you don’t fall
into the trap
of thinking it is always the degree of the first term. This
polynomial
is not written in standard form (descending order). So we had to
actually go to the second term to get the highest degree.
Since there are two terms, this is a binomial. |
 Example
3: Find the degree of the polynomial and
indicate
whether the polynomial is a monomial, binomial, trinomial, or none of
these:
-20. Example
3: Find the degree of the polynomial and
indicate
whether the polynomial is a monomial, binomial, trinomial, or none of
these:
-20.
 View a video of this example View a video of this example
|
Since the degree of the polynomial is the highest
degree of all the
terms, it looks like the degree is 0.
Since there is one term, this is a monomial. |
Recall that like terms are terms that have the
exact same variables
raised to the exact same exponents. One example of like terms
is 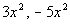 . Another
example is 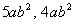 .
You can only combine terms that are like terms.
You can
think of it as the reverse of the distributive property.
It is like counting apples and oranges. You
just count up how
many variables you have the same and write the number in front of
the common variable part. |
|
Adding and Subtracting
Polynomials
|
If there is only a + sign in front of ( ), then the
terms inside of
( ) remain the same when you remove the ( ).
If there is a - in front of the ( ), then distribute it
by multiplying
every term in the ( ) by a -1 (or you can think of it as negating every
term in the ( )). |
Step 2:
Combine
like terms. |
|
*Remove the ( )
*Add like terms together
|
|
*Dist. the - through second ( )
*Combine like terms
|
In general, when multiplying two polynomials
together, use the distributive
property until every term of one polynomial is multiplied times every
term
of the other polynomial. Make sure that you simplify your
answer
by combining any like terms. On this page we will look at some of the more common
types of polynomials
to illustrate this idea. |
In this case, there is only one term in each
polynomial. You
simply multiply the two terms together. |
In this case, there is only one term in one
polynomial and more
than one term in the other. You need to distribute the monomial
to
EVERY term of the other polynomial. |
In this case, both polynomials have two terms.
You need to
distribute both terms of one polynomial times both terms of the other
polynomial.
One way to keep track of your distributive property
is to use the FOIL method. Note that this method
only works
on (Binomial)(Binomial).
|
F
|
First terms
|
|
O
|
Outside terms
|
|
I
|
Inside terms
|
|
L
|
Last terms
|
This is a fancy way of saying to take every term of
the first binomial
times every term of the second binomial. In other words, do the
distributive
property for every term in the first binomial. |
|
*Use the FOIL method
*Combine like terms
|
|
Binomial Squared
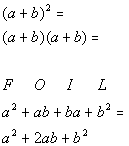
Special product rule for
a binomial squared:
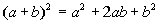
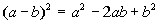
|
In other words, when you have a binomial squared,
you end up with
the first term squared plus (or minus) twice the product of the two
terms
plus the last term squared.
Any time you have a binomial squared you can use this
shortcut method
to find your product.
This is a special products rule. It would be
perfectly ok to use
the foil method on this to find the product. The reason we are
showing
you this form is that when you get to factoring, you will have to
reverse
your steps. So when you see 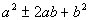 ,
you will already be familiar with the product it came from. ,
you will already be familiar with the product it came from. |
|
*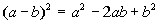 |
Product of the sum and
difference
of two terms
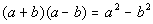
|
This is another special products rule. It would
be perfectly
ok to use the foil method on this to find the product. The reason
we are showing you this form is that when you get to factoring, you
will
have to reverse your steps. So when you see a difference of two
squares,
you will already be familiar with the product it came from. |
|
*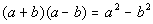 |
As mentioned above, use the distributive property
until every term
of one polynomial is multiplied by every term of the other polynomial.
Make sure that you simplify your answer by combining any like terms. |
|
*Use Dist. Prop. twice
*Combine like terms
|
Special product rule for
binomial cubed:
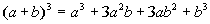
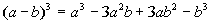
|
In other words, when you have a binomial cubed, you
end up with
the first term cubed plus (or minus) three times the first term squared
times the second term plus three times the first term times the second
term squared plus (or minus) the last term cubed.
Any time you have a binomial cubed you can use this
shortcut method
to find your product. |
|
*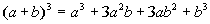 |
 Practice Problems Practice Problems
These are practice problems to help bring you to the
next level.
It will allow you to check and see if you have an understanding of
these
types of problems. Math works just like
anything
else, if you want to get good at it, then you need to practice
it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the
problem out on
your own and then check your answer by clicking on the link for the
answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1c: Find the degree of the polynomial and
indicate whether
the polynomial is a monomial, binomial, trinomial, or none of these. Practice
Problems 1a - 1c: Find the degree of the polynomial and
indicate whether
the polynomial is a monomial, binomial, trinomial, or none of these.
 Practice
Problems 2a - 2e: Perform the indicated operation. Practice
Problems 2a - 2e: Perform the indicated operation.
 Need Extra Help on these Topics? Need Extra Help on these Topics?

Videos at this site were created and produced by Kim Seward and Virginia Williams Trice.
Last revised on Dec. 13, 2009 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.
|
|


