College Algebra
Tutorial 2: Integer Exponents
|
WTAMU > Virtual Math Lab > College Algebra
 Learning Objectives Learning Objectives
After completing this tutorial, you should be able to:
-
Use the definition of exponents.
- Simplify exponential expressions involving multiplying like bases, zero
as an exponent, dividing like bases, negative exponents, raising a base
to two exponents, raising a product to an exponent and raising a
quotient
to an exponent.
|
 Introduction Introduction
This tutorial covers the basic definition and rules of
exponents.
The rules it covers are the product rule, quotient rule, power rule,
products
to powers rule, quotients to powers rule, as well as the definitions for
zero and negative exponents. Exponents are everywhere in algebra and
beyond.
Let's see what we can do with exponents. |
 Tutorial Tutorial
Definition of Exponents
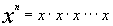
(note there are n x's
in the product)
x = base, n =
exponent
|
| Exponents are
another way to
write multiplication.
The exponent tells you how many times a base appears in
a PRODUCT.
 Example
1: Evaluate Example
1: Evaluate 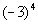 . .
 View a video of this example View a video of this example
|
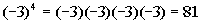 |
*Write the base -3 in a
product 4 times
*Multiply |
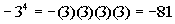 |
*Negate 3 to the fourth
*Put a - in front of 3 written in
a product
4 times
*Multiply |
| Hey, this looks a lot like example 1!!!!
It may look alike, but they ARE NOT exactly the
same. Can you
see the difference between the two?? Hopefully, you noticed that
in example 1, there was a ( ) around the - and the 3. In this
problem,
there is no ( ). This means the - is NOT part of the base, so it
will
not get expanded like it did in example 1.
It is interpreted as finding the negative or opposite
of 3 to the
fourth power. |
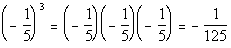 |
*Write the base -1/5 in a
product 3 times
*Multiply |
|
Multiplying Like Bases With
Exponents
(The Product Rule for Exponents)
Specific Illustration |
| Let’s first start by using the definition
of exponents
to help you to understand how we get to the law for multiplying like
bases
with exponents:
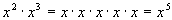
Note that 2 + 3 = 5, which is the exponent we ended up
with. We
had 2 x’s written in a product plus
another
3 x’s written in the product for a total
of
5 x’s in the product. To indicate
that
we put the 5 in the exponent.
Let's put this idea together into a general rule: |
|
Multiplying Like Bases With
Exponents
(Product Rule for Exponents)
in general,
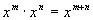
|
| In other words, when you
multiply like bases
you add your exponents.
The reason is, exponents count how many of your base
you have in
a product. So if you are continuing that product, you are adding
on to the exponents.
 Example
4: Use the product rule to simplify the
expression Example
4: Use the product rule to simplify the
expression  . .
 View a video of this example View a video of this example
|
|
*When mult. like bases you add
your exponents |
|
*When mult. like bases you add
your exponents
|
|
Zero as an exponent
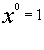
|
Except for 0, any base raised
to the 0 power
simplifies to be the number 1.
Note that the exponent doesn’t become 1, but the whole
expression simplifies
to be the number 1.
 Example
6: Evaluate Example
6: Evaluate 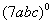 . .
 View a video of this example View a video of this example
|
|
*Any expression raised to the
0 power simplifies
to be 1 |
Be careful on this example. Order of operations
says to evaluate
exponents before doing any multiplication. This means we need to
find x raised to the 0 power first and
then
multiply it by -15. |
|
*x raised
to the
0 power is 1
*Multiply
|
Dividing Like Bases With
Exponents
(Quotient Rule for Exponents)
Specific Illustration
|
Let’s first start by using the definition
of exponents
to help you to understand how we get to the law for dividing like bases
with exponents:
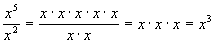
Note how 5 - 2 = 3, the final answer’s exponent.
When you multiply
you are adding on to your exponent, so it should stand to reason that
when
you divide like bases you are taking away from your exponent.
Let's put this idea together into a general rule: |
Dividing Like Bases With
Exponents
(Quotient Rule for Exponents)
in general,
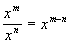
|
In other words, when you
divide like bases
you subtract their exponents.
Keep in mind that you always take the numerator’s
exponent minus your
denominator’s exponent, NOT the other way around.
 Example
8: Find the quotient Example
8: Find the quotient 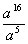 . .
 View a video of this example View a video of this example
|
|
*When div. like bases you subtract
your exponents
|
|
*When div. like bases you
subtract your exponents
|
Negative Exponents
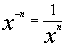 or
or 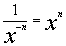 |
Be careful with negative
exponents. The
temptation is to negate the base, which would not be a correct thing to
do. Since exponents
are another
way to write multiplication and the negative is in the exponent, to
write
it as a positive exponent we do the multiplicative inverse which is to
take the reciprocal of the base.
 Example
10: Simplify Example
10: Simplify 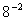 . .
 View a video of this example View a video of this example
|
|
*Rewrite with a pos. exp. by
taking recip.
of base
*Use def. of
exponents
to evaluate |
|
*Rewrite with a pos. exp. by
taking recip.
of base
*Use def. of
exponents
to evaluate |
|
Base Raised to Two Exponents
(Power Rule for Exponents)
Specific Illustration
|
|
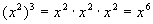
Note how 2 times 3 is 6, which is the exponent of the
final answer.
We can think of this as 3 groups of 2, which of course would come out
to
be 6. |
Base Raised to two Exponents
(Power Rule for Exponents)
in general,
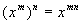
|
In other words, when you
raise a base to two
exponents, you multiply those exponents together.
Again, you can think of it as n
groups of
m
if it helps you to remember.
 Example
12: Simplify Example
12: Simplify 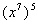 . .
 View a video of this example View a video of this example
|
|
*When raising a base to two
powers you mult.
your exponents |
|
A Product Raised to an Exponent
(Products to Powers Rule for Exponents)
Specific Illustration
|
Let’s first start by using the definition
of exponents
to help you to understand how we get to the law for raising a product
to
an exponent:
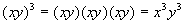
Note how both bases of your product ended up being
raised by the exponent
of 3. |
A Product Raised to an Exponent
(Products to Powers Rule for Exponents)
in general,
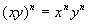
|
In other words, when you have
a PRODUCT (not
a sum or difference) raised to an exponent, you can simplify by raising
each base in the product to that exponent.
 Example
14: Simplify Example
14: Simplify 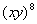 . .
 View a video of this example View a video of this example
|
|
*When raising a product to an
exponent, raise
each base of the product to that exponent |
|
*When raising a product to an
exponent, raise
each base of the product to that exponent
*Mult. exponents when using power
rule for exponents |
|
A Quotient Raised to an Exponent
(Quotients to Powers Rule for Exponents)
Specific Illustration
|
Let’s first start by using the definition
of exponents
to help you to understand how we get to the law for raising a quotient
to an exponent:
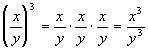
Since division is really multiplication of the
reciprocal, it has the
same basic idea as when we raised a product to an exponent. |
A Quotient Raised to an Exponent
(Quotients to Powers Rule for Exponents)
in general,
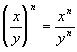
|
In other words, when you have
a QUOTIENT (not
a sum or difference) raised to an exponent, you can simplify by raising
each base in the numerator and denominator of the quotient to that
exponent.
 Example
16: Simplify Example
16: Simplify 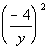 . .
 View a video of this example View a video of this example
|
|
*When raising a quotient to an
exponent, raise
each base of the quotient to that exponent
*Use def. of
exponents
to evaluate |
Of course, we all know that life isn’t so cut and
dry. A lot
of times you need to use more than one definition or law of exponents
to
get the job done. What we did above was to
set the foundation to make sure you have a good understanding of the
different
ideas associated with exponents. Next we will work through
some problems which will intermix these different laws. |
|
Simplifying an Exponential
Expression |
When simplifying an exponential expression,
write it so that
each base is written one time with one POSITIVE exponent.
In other words, write it in the most condensed form you
can making sure
that all your exponents are positive.
A lot of times you have to use more than one rule to get
the job done.
As long as you use the rule appropriately you should be fine. |
Be careful going into the last line. Since b
doesn't
have a negative exponent, we DO NOT take the reciprocal of b.
The other bases each have a negative exponent, so those bases we have
to
take the reciprocal of. |
 Practice Problems Practice Problems
These are practice problems to help bring you to the
next level.
It will allow you to check and see if you have an understanding of
these
types of problems. Math works just like
anything
else, if you want to get good at it, then you need to practice
it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice.
To get the most out of these, you should work the
problem out on
your own and then check your answer by clicking on the link for the
answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1f: Simplify the exponential expression. Practice
Problems 1a - 1f: Simplify the exponential expression.
 Need Extra Help on these Topics? Need Extra Help on these Topics?

Videos at this site were created and produced by Kim Seward and Virginia Williams Trice.
Last revised on Feb. 15, 2008 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.
|


