College Algebra
Answer/Discussion to Practice Problems
Tutorial 52: Solving Systems of Nonlinear Equations
in Two Variables

WTAMU > Virtual Math Lab > College Algebra > Tutorial 52: Solving Systems of Nonlinear Equations in Two Variables

Answer/Discussion to 1a

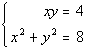
problem 1a

I'm going to chose to use the substitution method.

Not that because of the terms involved, it would not be possible to work this problem using the process of elimination.

Step 1: Simplify if needed.

Both of these equations are already simplified. No work needs to be done here.

Step 2: Solve one equation for either variable.

It does not matter which equation or which variable you choose to solve for. Just keep it simple.

I'm going to chose to use the first equation to solve for y.

Solving the first equation for y we get:

*1st equation solved for y

Step 3: Substitute what you get for step 2 into the other equation
AND
Step 4: Solve for the remaining variable .

Substitute the expression 4/x for y into the second equation and solve for x:
(when you plug in an expression like this, it is just like you plug in a number for your variable)

*Sub. 4/x in for y

*Factor the trinomial

*Factor the difference of squares

*Set 1st factor = 0

*Set 2nd factor = 0

Step 5: Solve for second variable.

Plug in both values found for x in step 4.

Plug in -2 for x into the equation in step 2 to find y's value.

*Plug in -2 for x

(-2, -2) is one solution to this system.

Plug in 2 for x into the equation in step 2 to find y's value.

*Plug in 2 for x

(2, 2) is another solution to this system.

Step 6: Check the proposed ordered pair solution(s) in BOTH original equations.

You will find that if you plug either the ordered pair (-2, -2) OR (2, 2) into BOTH equations of the original system, that they are both a solution to BOTH of them.

(-2, -2) and (2, 2) are both a solution to our system.

(return to problem 1a)

Answer/Discussion to 1b

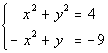
problem 1b

I'm going to chose to use the elimination by addition method, however it would be perfectly find for you to use the substitution method. Either way the answer will be the same.

Step 1: Simplify if needed.

Both of these equations are already simplified. No work needs to be done here.

Step 2: Multiply one or both equations by a number that will create opposite coefficients for like terms if needed.

Again, you want to make this as simple as possible.

The variable that you want to eliminate must be a like variable. Note that x squareds' coefficients are already opposites. So we do not have to multiply either equation by a number.

Also note that the y terms are not like terms so we would not be able to eliminate y in this problem.

Here is the original problem complete with opposite coefficients for the x squared terms:

Step 3: Add equations.

*Note that x squareds dropped out

Step 4: Solve for remaining variable.

*Setting the quadratic = 0

Note that this does not factor, so I'm going to have to use drastic majors - yes the Quadratic Formula.

If you need a review on the quadratic formula feel free to go to Tutorial 17: Quadratic Equations.

*Identifying a, b, and c for the quad. form.

*Plugging a, b, and c into the quad form.

*Simplifying radicand, which is a negative number

Note how we came up with a negative underneath the square root.

That means there is NOT a real number solution for this.

Step 5: Solve for second variable.

There is no value to plug in here.

Step 6: Check the proposed ordered pair solution(s) in BOTH original equations.

There are no ordered pairs to check.

The answer is no solution.

(return to problem 1b)

Answer/Discussion to 1c

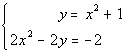
problem 1c

I'm going to chose to use the substitution method, however it would be perfectly find for you to use the elimination by addition method. Either way the answer will be the same.

Step 1: Simplify if needed.

Both of these equations are already simplified. No work needs to be done here.

Step 2: Solve one equation for either variable.

Note how the first equation is already solved for y. We can use that one for this step.

It does not matter which equation or which variable you choose to solve for. But it is to your advantage to keep it as simple as possible.

First equation solved for y:

*Solved for y

Step 3: Substitute what you get for step 2 into the other equation
AND
Step 4: Solve for the remaining variable.

Substitute the expression for y into the second equation and solve for x:
(when you plug in an expression like this, it is just like you plug in a number for your variable)

*Sub. x^2 + 1 for y
*Distribute -2 through ( )

*Variable dropped out AND true

Wait a minute, where did our variable go????

As mentioned before, if the variable drops out AND we have a TRUE statement, then when have an infinite number of solutions. They end up being the same line.

Step 5: Solve for second variable.

Since we did not get a value for x, there is nothing to plug in here.

Step 6: Check the proposed ordered pair solution(s) in BOTH original equations.

There is no value to plug in here.

When they end up being the same equation, you have an infinite number of solutions. You can write up your answer by writing out either equation to indicate that they are the same equation.

Two ways to write the answer are OR .

(return to problem 1c)

WTAMU > Virtual Math Lab > College Algebra >Tutorial 52: Solving Systems of Nonlinear Equations in Two Variables