College Algebra
Tutorial 52: Solving Systems of
Nonlinear Equations
in Two Variables
 Learning Objectives Learning Objectives
After completing this tutorial, you should be able to:
- Solve a system of nonlinear equations in two variables by the substitution
method.
- Solve a system of nonlinear equations in two variables by the elimination
by addition method.
|
 Introduction Introduction
In this tutorial we will be specifically looking at systems of nonlinear
equations that have two equations and two unknowns. We will look
at solving them two different ways: by the substitution method and
by the elimination by addition method. These methods will be
done in the same manner that they are done with systems of linear equations,
we will just be applying it to nonlinear systems in this tutorial.
If you need a review on solving systems of linear equations in two variables,
feel free to go to Tutorial 49: Solving
Systems of Linear Equations in Two Variables. So, let's go
ahead and look at these systems. |
 Tutorial Tutorial
|
System of Nonlinear Equations
|
A system of nonlinear equations is two or more equations, at least
one of which is not a linear equation, that are being solved simultaneously.
Note that in a nonlinear system, one of your equations can be linear,
just not all of them.
In this tutorial, we will be looking at systems that have only two equations
and two unknowns. |
In general, a solution of a system in two variables is an ordered
pair that makes BOTH equations true.
In other words, it is where the two graphs intersect, what they have
in common. So if an ordered pair is a solution to one equation, but
not the other, then it is NOT a solution to the system.
Since we are looking at nonlinear systems, in some cases, there may
be more than one ordered pair that satisfies all equations in the system.
A consistent system is a system that has at least one solution.
An inconsistent system is a system that has no solution.
The equations of a system are dependent if ALL the solutions
of one equation are also solutions of the other equation. In other
words, they end up being the same graph.
The equations of a system are independent if they do not share
ALL solutions. They can have one point in common, just not all
of them. |
There are three possible outcomes that you
may encounter when working with these systems:
-
-
-
|
Finite Number of Solutions
If the system in two variables has one solution, it is an ordered
pair that is a solution to BOTH equations. In other words, when
you plug in the values of the ordered pair it makes BOTH equations TRUE.
Since we are looking at nonlinear systems, in some cases there may
be more than one ordered pair that satisfies all equations in the system.
If you do get a finite number of solutions for your final answer, is
this system consistent or inconsistent?
If you said consistent, give yourself a pat on the back!
If you do get a finite number of solutions for your final answer, would
the equations be dependent or independent?
If you said independent, you are correct!
The graph below illustrates a system of two equations and two unknowns
that has four solutions:
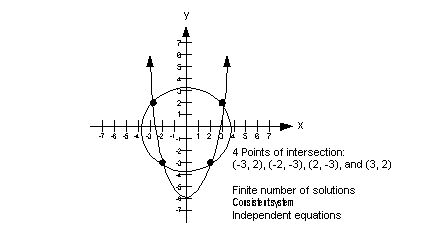
|
No Solution
In some cases, the equations in the system will not have any points
in common. In this situation, you would have no solution.
If you get no solution for your final answer, is
this system consistent or inconsistent?
If you said inconsistent, you are right!
If you get no solution for your final answer, would
the equations be dependent or independent?
If you said independent, you are correct!
The graph below illustrates a system of two equations and two unknowns
that has no solution:
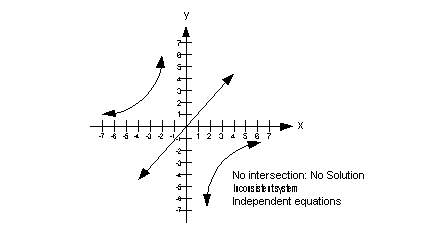
|
Infinite Solutions
If the two graphs end up lying on top of each other, then there
is an infinite number of solutions. In this situation, they would
end up being the same graph, so any solution that would work in one equation
is going to work in the other.
If you get an infinite number of solutions for your final answer, is
this system consistent or inconsistent?
If you said consistent, you are right!
If you get an infinite number of solutions for your final answer, would
the equations be dependent or independent?
If you said dependent, you are correct!
The graph below illustrates a system of two equations and two unknowns
that has an infinite number of solutions:
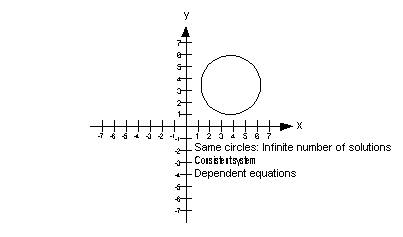
|
|
Solve by the Substitution Method
|
Step 1: Simplify if needed. |
This would involve things like removing ( ) and removing fractions.
To remove ( ): just use the distributive property.
To remove fractions: since fractions are another way to write division,
and the inverse of divide is to multiply, you remove fractions by multiplying
both sides by the LCD of all of your fractions. |
Step 2: Solve one
equation for either variable. |
It doesn't matter which equation you use or which variable you choose
to solve for.
You want to make it as simple as possible. If one of the equations
is already solved for one of the variables, that is a quick and easy way
to go.
If you need to solve for a variable, then try to pick one that has a
1 or -1 as a coefficient. That way when you go to solve for it, you
won't have to divide by a number and run the risk of having to work with
a fraction (yuck!!).
Also, it is easier to solve for a variable that is to the 1 power, as
opposed to being squared, cubed, etc. |
Step 3: Substitute what
you get for step 2 into the other equation. |
This is why it is called the substitution method. Make sure that
you substitute the expression into the OTHER equation, the one you didn't
use in step 2. This will give you one equation with one unknown. |
Step 4: Solve for
the remaining variable. |
Solve the equation set up in step 3 for the variable that is left.
Most of the equations in this step will end up being either linear or
quadratic. Once in awhile you will run into a different type of equation.
If you need a review on solving linear or quadratic equations, feel
free to go to Tutorial 14: Linear
Equations in On Variable or Tutorial
17: Quadratic Equations.
Keep in mind that when you go to solve for this variable that you may
end up with no solution for your answer. For example, you may end
up with your variable equaling the square root of a negative number, which
is not a real number, which means there would be no solution.
If your variable drops out and you have a FALSE statement, that means
your answer is no solution.
If your variable drops out and you have a TRUE statement, that means
your answer is infinite solutions, which would be the equation of the line. |
Step 5: Solve for
second variable. |
If you come up with a finite number of values for the variable in
step 4, that means the two equations have a finite number of solutions.
Plug the value(s) found in step 4 into any of the equations in the problem
and solve for the other variable. |
Step 6: Check the proposed
ordered pair solution(s) in BOTH original equations. |
You can plug in the proposed solution(s) into BOTH equations.
If it makes BOTH equations true, then you have your solution to the system.
If it makes at least one of them false, you need to go back and redo
the problem. |
 Example
1 Example
1: Solve the system of equations by the substitution method:
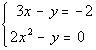 |
Both of these equations are already simplified. No work needs
to be done here. |
It does not matter which equation or which variable you choose to solve
for. Just keep it simple.
Since the y in the first equation has a
coefficient of -1, that would mean we would not run the risk of having
to work with fractions (YUCK). The easiest route here is to solve
the first equation for y, and we definitely
want to take the easy route.
You would not be wrong to either choose the other equation and/or solve
for x, again you want to keep it as simple
as possible.
Solving the first equation for y we get: |
|
*1st equation solved for y |
Substitute the expression 3x + 2 for y into the second equation and solve for x:
(when you plug in an expression like this, it is just like you plug
in a number for your variable) |
|
*Set 1st factor = 0
*Set 2nd factor = 0
|
Plug in both values found for x in step 4. |
Plug in -1/2 for x into the equation
in step 2 to find y's value. |
(-1/2, 1/2) is one solution to this system.
Plug in 2 for x into the equation in
step 2 to find y's value. |
(2, 8) is another solution to this system. |
You will find that if you plug either the ordered pair (-1/2, 1/2)
OR (2, 8) into BOTH equations of the original system, that they are both
a solution to BOTH of them.
(-1/2, 1/2) and (2, 8) are both a solution to our system. |
 Example
2 Example
2: Solve the system of equations by the substitution method:
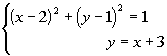 |
Even though we have ( ) in this problem, since we are going to do this
by substitution, we do not need to clear them at this point to be able
to do step 2. |
Note how the second equation is already solved for y.
We can use that one for this step.
It does not matter which equation or which variable you choose to solve
for. But it is to your advantage to keep it as simple as possible.
Second equation solved for y: |
Substitute the expression x + 3 for y into the first equation and solve for x:
(when you plug in an expression like this, it is just like you plug
in a number for your variable) |
|
*Sub. x + 3 for y
*Square both binomials to clear the (
)
*Solve using the Square
Root Method
*Solved for x
|
Wait a minute, there is an i in the answer.
As mentioned above, in some cases we end up with no solution.
Here is an example where even though we came up with two values for x,
we did not come up with a real number answer for a variable. This
means there is no solution. |
Since we did not get a real number for x,
there is nothing to plug in here. |
There are no ordered pairs to check.
The answer is no solution. |
|
Solve by the Elimination by Addition Method
|
Step 1: Simplify if needed. |
This would involve things like removing ( ) and removing fractions.
To remove ( ): just use the distributive property.
To remove fractions: since fractions are another way to write division,
and the inverse of divide is to multiply, you remove fractions by multiplying
both sides by the LCD of all of your fractions. |
Step 2: Multiply one
or both equations by a number that will create opposite coefficients for
like terms if needed. |
Looking ahead, we will be adding these two equations together.
In that process, we need to make sure that one of the variables drops out,
leaving us with one equation and one unknown. The only way we can
guarantee that is if we are adding opposites. The sum of opposites
is 0.
If neither variable drops out, then we are stuck with an equation with
two unknowns which is unsolvable.
It doesn't matter which variable you choose to drop out.
You want to keep it as simple as possible. If a variable already
has opposite coefficients than go right to adding the two equations together.
If they don't, you need to multiply one or both equations by a number that
will create opposite coefficients in one of your variables. You can
think of it like a LCD. Think about what number the original coefficients
both go into and multiply each separate equation accordingly. Make
sure that one variable is positive and the other is negative before you
add.
For example, if you had a 2x in one equation
and a 3x in another equation, we could multiply
the first equation by 3 and get 6x and the
second equation by -2 to get a -6x. So
when you go to add these two together they will drop out.
Since we are working with nonlinear systems here, you need to keep
in mind that the variable that you want to eliminate must be a like variable.
In other words, it must not only be the same variable, but have the same
exponent. For example, you can not combine 2x with -2x squared, they are not like terms.
But you can combine 2x squared with -2x squared or 2x with -2x.
This will play a big part on your decision as to what to eliminate.
So even though in general, it doesn't matter
what variable you choose to drop out, sometimes the problem will dictate
that decision for you, because you are unable to eliminate one of the variables
because they are not like terms. |
Add the two equations together.
The variable that has the opposite coefficients will drop out in this
step and you will be left with one equation with one unknown. |
Step 4: Solve for remaining
variable. |
Solve the equation found in step 3 for the variable that is left.
Most of the equations in this step will end up being either linear or
quadratic. Once in awhile you will run into a different type of equation.
If you need a review on solving linear or quadratic equations, feel
free to go to Tutorial 14: Linear
Equations in On Variable or Tutorial
17: Quadratic Equations.
Keep in mind that when you go to solve for this variable that you may
end up with no solution for your answer. For example, you may end
up with your variable equaling the square root of a negative number, which
is not a real number, which means there would be no solution.
If both variables drop out and you have a FALSE statement, that means
your answer is no solution.
If both variables drop out and you have a TRUE statement, that means
your answer is infinite solutions, which would be the equation of the line. |
Step 5: Solve for second
variable. |
If you come up with a finite number of values for the variable in
step 4, that means the two equations have a finite number of solutions.
Plug the value(s) found in step 4 into any of the equations in the problem
and solve for the other variable. |
Step 6: Check the proposed
ordered pair solution(s) in BOTH original equations. |
You can plug the proposed solution(s) into BOTH equations. If
it makes BOTH equations true, then you have your solution to the system.
If it makes at least one of them false, you need to go back and redo
the problem. |
 Example
3 Example
3: Solve the system of equation by the elimination method:
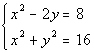 |
Both of these equations are already simplified. No work needs
to be done here. |
Again, you want to make this as simple as possible.
The variable that you want to eliminate must be a like variable. In other words, it must not only be the same variable, but have the same
exponent. Note how x is squared on both
equations. So we would be able to get opposite coefficients on them
and then when we added the two equations together they would drop out.
Note how y is to the one power in the first
equation and squared on the second equation. If we would pick y to eliminate we would have a problem because we cannot combine unlike terms
together. y squared -y would be y squared - y NOT 0.
So I proposed that we multiply the second equation by -1, this
would create a 1 and a -1 in front of the x squareds and we will have our opposites.
Multiplying the second equation by -1 we get: |
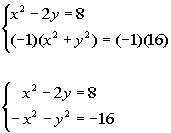 |
*Mult. both sides of 2nd eq. by -1
*x squareds have
opposite coefficients
|
|
*Note that x squareds
dropped out
|
|
*Set first factor = 0
*Set second factor = 0
|
You can choose any equation used in this problem to plug in the found y values.
I choose to plug in -4 for y into the
first equation to find x's value. |
So (0, - 4) is one solution to this system. |
I choose to plug in -4 for y into the
first equation to find x's values. |
So 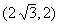 and and 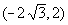 are two more solutions to this system. are two more solutions to this system. |
You will find that if you plug the ordered pairs (0, - 4), 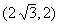 ,
and 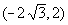 into BOTH equations
of the original system, that they would all be solutions to BOTH of them.
(0, - 4), 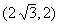 ,
and ,
and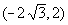 are all solutions
to our system. are all solutions
to our system. |
 Example
4 Example
4: Solve the system of equation by the elimination method:
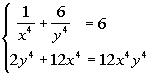 |
The first equation is full of those nasty fractions. We can simplify
it by multiplying it by its LCD, just like you can do when you are working
with one equation. As long as you do the same thing to both sides
of an equation, you keep the two sides equal to each other. Multiplying the first equation by its LCD we get: |
|
*Multiply 1st eq. by its LCD x^4y^4
|
Again, you want to make this as simple as possible.
The variable that you want to eliminate must be a like variable. Note
that we could either choose to eliminate the x to the fourth terms or the y to the fourth
terms or even the x to the fourth y to the fourth terms. I'm going to choose to eliminate the x to the fourth terms, which means I want opposite coefficient on those terms.
Looks like we just need to multiply the first equation by -2.
Multiplying the first equation by -2 we get: |
|
*Mult. both sides of 1st eq. by -2
*x to the fourths
have opposite coefficients
|
|
*Note that everything dropped out
|
Hey where did our variables go??
As mentioned above, if the variable drops out AND we have a TRUE statement,
then when have an infinite number of solutions. They end up being
the same graph. |
There is no value to plug in here. |
There is no value to plug in here.
When they end up being the same equation, you have an infinite number
of solutions. You can write up your answer by writing out either
equation to indicate that they are the same equation.
Two ways to write the answer are 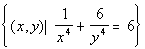 OR OR 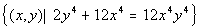 . . |
Special Note About Solving Nonlinear
Systems
Note that when solving these nonlinear systems, you may come across
some that you are unable to use the substitution method and some
that you are unable to use the elimination by addition method. Just
try what you feel may work and if it doesn't work try the other method. |
 Practice Problems Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice.
To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice Problems 1a - 1c: Solve each system by either the substitution
or elimination by addition method. Practice Problems 1a - 1c: Solve each system by either the substitution
or elimination by addition method.
 Need Extra Help on these Topics? Need Extra Help on these Topics?

Last revised on May 15, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.
|
|


