College Algebra
Tutorial 45: Exponential Equations
 Learning Objectives
After completing this tutorial, you should be able to:
- Solve exponential equations.
|
Introduction
In this tutorial I will walk you through how to solve equations that
have exponential expressions. In these equations, you will notice
that the variable that we are solving for is in the exponent. We
are use to seeing the variable in the base. We will using inverse
operations like we do in linear equations, the inverse operation we will
be using here is logarithms. If you need a review on the definition
of log functions, feel free to go to Tutorial
43: Logarithmic Functions. If you need a review on log properties,
feel free to go to Tutorial 44:
Logarithmic Properties. I think you are ready to get started. |
Tutorial
Solving Exponential Equations,
where x is in the exponent, BUT
the bases DO NOT MATCH.
|
Step 1: Isolate
the exponential expression. |
Get your exponential expression on one side everything outside of the
exponential expression on the other side of your equation. |
Step 2: Take the natural
log of both sides. |
The inverse operation of an exponential expression is a log.
Make sure that you do the same thing to both sides of your equation to
keep them equal to each other. |
Step 3: Use
the properties of logs to pull the x out of the exponent. |
Now that the variable is out of the exponent, solve for the variable
using inverse operations to complete the problem. |
Special Note:
The only way we can get that variable out of the exponent, when the
bases don't match up, is to use logs. The 3rd step allows us to do
this. When solving an equation, it doesn't matter what you do to
the equation as long as you do the same thing to both sides - this keeps
both sides equal. Also, the reason we take the natural log of both
sides is because we have the natural log key on the calculator - so we
would be able to find a value of it in the end. |
 Example
1: Solve the exponential equation  .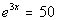
Round your answer to two decimal places. |
This is already done for us in this problem. |
|
*Take the natural log of BOTH sides |
|
*Inverse of mult. by 3lne is to divide by 3lne
*Use the calculator to find ln 50
*lne is 1
|
Example
2: Solve the exponential equation  .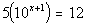
Round your answer to two decimal places. |
|
*Inverse of mult. by 5 is to divide by 5
*Exponential expression isolated
|
|
*Take the natural log of BOTH sides |
|
*Inverse of mult. by ln 10 is to divide by
ln 10
*Inverse of add 1 is sub. 1
*Use the calculator to find ln 2.4 and ln 10
|
Example
3: Solve the exponential equation  .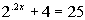
Round your answer to two decimal places. |
|
*Inverse of add 4 is sub. 4
*Exponential expression isolated |
|
*Take the natural log of BOTH sides |
|
*Inverse of mult. by .2ln 2 is to divide by
.2ln 2
*Use the calculator to find ln 21 and ln 2
|
Example
4: Solve the exponential equation  .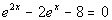
Round your answer to two decimal places. |
Notice how we have two exponential terms that have different exponents.
We wouldn't be able to isolate both. We will have to figure out another
way to rewrite it so we can continue with the steps.
Note how we have a trinomial and that e to the 2x is e to the x squared. This means it is quadratic
in from. So we can factor it just like a trinomial of the form  . |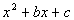
|
*Set the 1st factor = 0
*Isolate the exponential expression
*Set the 2nd factor = 0
*Isolate the exponential expression
|
Note that since e is a positive base, no matter what the exponent is on x,
this exponential expression CANNOT equal -2.
So there is only one equation that we can solve  . |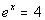
|
*Take the natural log of BOTH sides |
|
*Inverse of mult. by lne is to divide by lne
*Use the calculator to find ln 4
*lne = 1
|
Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice.
To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice Problems 1a - 1c: Solve the given exponential equation. Round
your answer to two decimal places.
Need Extra Help on these Topics?
Last revised on March 24, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.
|
|
