College Algebra
Tutorial 44: Logarithmic Properties
 Learning Objectives
After completing this tutorial, you should be able to:
- Be familiar with and use properties of logarithms in
various
situations.
|
Introduction
In this tutorial I am going to help you expand your
knowledge of logarithms.
Probably the biggest thing you need to remember to help you out with
this
section is that LOGS ARE ANOTHER WAY TO WRITE
EXPONENTS. If you keep that little tidbit of
information
at the forefront of your brain, that will help you out TREMENDOUSLY
through
this section. Ok, here we go. |
Tutorial
As mentioned above - and I can’t emphasize this enough
- logs are
another way to write exponents. If you understand that
concept
it really does make things more pleasant when you are working with
logs. |
Property 1
Product Rule
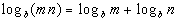
m > 0 and n > 0
|
Basically, what we are saying here is that another
way to write
the log of a product is to take the log of the first base and add it to
the log of the second base.
Hmmmm, why don’t I just take the product of their
logs??????
Wait a minute, I remember my teacher saying above that
logs are another
way to write exponents - WHENEVER I WAS MULTIPLYING LIKE BASES, I
ADDED MY EXPONENTS - SO I’M GOING TO HAVE TO ADD MY LOGS -
EUREKA!!!!
Note that even though m and n are not the bases of the log itself, they can each be written as base b to an exponent, because of the definition of logarithms. |
Here is a quick illustration of how this property
works:
|
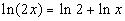
Property 2
Quotient Rule
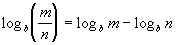
m > 0 and n > 0
|
Basically, what we are saying here is that another
way to write
the log of a quotient is to take the log of the numerator and subtract
the log of the denominator.
So here, we have to remember that when we were
dividing like bases,
we subtracted our exponents - so we do the same type of thing with our
logs. |
Here is a quick illustration of how this property
works:
|
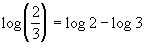
Property 3
Power Rule
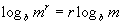
m > 0
|
Basically, what we are saying here is that whenever
you have a 2nd
exponent inside the log - remember the log itself is an exponent - then
you can pull it out front and multiply it times the log.
Wow, that looks a little different, but again it comes
from the fact
that logs are another way to write exponents.
Remember that when we had a base raised to 2 powers
that we would
multiply those 2 exponents together. That is what we are doing
here.
Again, even though m is not the base of
the
log, it can be written as b to an
exponent
(based on the log definition) and the log itself is an exponent so we
have
a double exponent - so we multiply our exponents together. |
Here is a quick illustration of how this property
works:
|
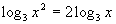
Property 4
Change of Base Formula
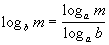
m > 0 and b > 0
|
Basically, what we are saying here is, whenever you
need to change
the base of your log you can rewrite it as the log base a (whatever the
new base is) of the original inside over the log base a (whatever the
new
base is) of the original base.
Your calculator is limited to only finding base 10 and
base e logarithms. That would leave us in a bind if we needed to find
the
value of a log with any other base. So we can use this
change-of-base
formula to change it to base 10 or e so
we
could find a value. Neat, huh? |
Here is a quick illustration of how this property
works:
|
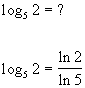
 Example
1: Expand 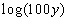 as much as possible. Evaluate without a calculator where possible. |
Note how there is no base written. Does that mean
there is no
base? Not in the least.
What would the base be in this problem? If you
said 10 you are
correct. This is known as the common log.
If you need a review on the common log (log base 10),
feel free to go
to Tutorial 43:
Logarithmic
Functions. |
Example
2: Expand 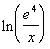 as much as possible. Evaluate without a calculator where possible. |
Note how there is a ln and no base written.
What would the base be in this problem? If you
said e you are correct. This is known as the natural log.
If you need a review on the natural log (log base e),
feel free to go to Tutorial
43: Logarithmic Functions. |
Example
3: Expand 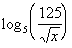 as much as possible. Evaluate without a calculator where possible. |
What is the base in this problem?
This time the base is 5. Make sure that you keep
that same base
throughout the problem. |
Example
4: Expand 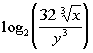 as much as possible. Evaluate without a calculator where possible. |
What is the base in this problem?
This time the base is 2. Make sure that you keep
that same base
throughout the problem. |
Example
5: Condense 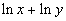 into one logarithmic expression. Evaluate without a calculator
where
possible. |
This time we are going in reverse of what we did in
examples 1 - 4.
However, you can use the same properties we used on them. You can
use those properties in either direction.
What is the base in this problem?
This time the base is e.
Make sure
that you keep that same base throughout the problem. |
Example
6: Condense 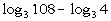 into one logarithmic expression. Evaluate without a calculator
where
possible. |
Again we are going in reverse of what we did in
examples 1 - 4.
What is the base in this problem?
This time the base is 3. Make sure that you keep
that same base
throughout the problem. |
Example
7: Condense 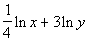 into one logarithmic expression. Evaluate without a calculator
where
possible. |
Again we are going in reverse of what we did in
examples 1 - 4.
What is the base in this problem?
This time the base is e.
Make sure
that you keep that same base throughout the problem. |
Example
8: Rewrite 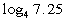 using natural logarithms and evaluate using a calculator. Round
to
4 decimal places. |
Note that the calculator can only evaluate logs that
are base 10 or
base e. Since this problem is in
base
4, we need to change the base to base e (or base 10). Since the instructions say base e,
let's do that.
This should land between 1 and 2, because 7.25 lands
between 4^1 = 4
and 4^2 = 16. Again logs are another way to write exponents and
that
is what we are looking for here. |
|
*Use the calculator to find ln
7.25 and ln
4
*Divide |
Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice.
To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice Problems 1a - 1c: Expand each logarithmic
expression as much as
possible. Evaluate without a calculator where possible.
Practice Problems 2a - 2b: Condense each logarithmic expression
into one logarithmic
expression. Evaluate without a calculator where possible.
Practice Problem 3a: Rewrite the logarithmic expression
using natural logarithms
and evaluate using a calculator. Round to 4 decimal places.
Need Extra Help on these Topics?
Last revised on March 23, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.
|
|
