College Algebra
Answer/Discussion to Practice Problems
Tutorial 20: Equations that are Quadratic in Form

WTAMU > Virtual Math Lab > College Algebra > Tutorial 20: Equations that are Quadratic in Form

Answer/Discussion to 1a

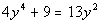
Step 1: Write in Standard Form, 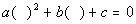, if needed.

*Inverse of add. 13 y squared is sub. 13 y squared

*Equation in standard form

Step 2: Substitute a variable in for the expression that follows b in the second term.

Below, I have the original equation rewritten in a way to show you that it is quadratic in form. Note how when you square y squared you get y to the fourth, which is what you have in the first term.

*Rewriting original equation to show it is quadratic in form
*Note that (y squared) squared = y to the fourth

*When in stand. form, let t = the expression following b.

Next, we need to substitute t in for y squared in the original equation.

*Original equation

*Substitute t in for y squared

Note how we ended up with a quadratic equation when we did our substitution. From here, we need to solve the quadratic equation that we have created.

Step 3: Solve the quadratic equation created in step 2.

You can use any method you want to solve the quadratic equation: factoring, completing the square or quadratic formula.

I'm going to factor it to solve it.

*Factor the trinomial

*Use Zero-Product Principle
*Set 1st factor = 0 and solve

*Set 2nd factor = 0 and solve

Step 4: Find the value of the variable from the original equation.

In step 2 we used the substitution of t = y squared.

Let's find the value(s) of y when t = 9/4:

*Plug in 9/4 for t
*Use square root method to solve for y

*First solution

*Second solution

Let's find the value(s) of y when t = 1:

*Plug in 1 for t
*Use square root method to solve for y

*First solution

*Second solution

Step 5: Check your solutions.

Let's double check to see if y = 3/2 is a solution to the original equation.

*Plugging in 3/2 for y

*True statement

Since we got a true statement, y = 3/2 is a solution.

Let's double check to see if y = -3/2 is a solution to the original equation.

*Plugging in -3/2 for y

*True statement

Since we got a true statement, y = -3/2 is a solution.

Let's double check to see if y = 1 is a solution to the original equation.

*Plugging in 1 for y
*True statement

Since we got a true statement, y = 1 is a solution.

Let's double check to see if y = -1 is a solution to the original equation.

*Plugging in -1 for y
*True statement

Since we got a true statement, y = -1 is a solution.

There are four solutions to this equation: y = 3/2, y = -3/2, y = 1, and y = -1.

(return to problem 1a)

Answer/Discussion to 1b

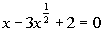
Step 1: Write in Standard Form, 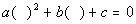, if needed.

This equation is already in standard form.

Step 2: Substitute a variable in for the expression that follows b in the second term.

Below, I have the original equation rewritten in a way to show you that it is quadratic in form. Note how when you square x to the 1/2 power you get x, which is what you have in the first term.

*Rewriting original equation to show it is quadratic in form
*Note that (x to the 1/2 power) squared = x

*When in stand. form, let t = the expression following b.

Next, we need to substitute t in for x to the 1/2 power in the original equation.

*Original equation

*Substitute t in for x to the 1/2 power

Note how we ended up with a quadratic equation when we did our substitution. From here, we need to solve the quadratic equation that we have created.

Step 3: Solve the quadratic equation created in step 2.

You can use any method you want to solve the quadratic equation: factoring, completing the square or quadratic formula.

I'm going to factor it to solve it.

*Factor the trinomial

*Use Zero-Product Principle
*Set 1st factor = 0 and solve

*Set 2nd factor = 0 and solve

Step 4: Find the value of the variable from the original equation.

In step 2 we used the substitution of t = x to the 1/2 power.

Let's find the value(s) of x when t = 2:

*Plug in 3 for t
*Solve the rational exponent equation

*Inverse of taking it to the 1/3 power is raising it to the 3rd power

Let's find the value(s) of x when t = 1:

*Plug in 1 for t
*Solve the rational exponent equation

*Inverse of taking it to the 1/2 power is raising it to the 2nd power

Step 5: Check your solutions.

Let's double check to see if x = 4 is a solution to the original equation.

*Plugging in 4 for x

*True statement

Since we got a true statement, x = 4 is a solution.

Let's double check to see if x = 1 is a solution to the original equation.

*Plugging in 1 for x

*True statement

Since we got a true statement, x = 1 is a solution.

There are two solutions to this equation: x = 4 and x = 1.

(return to problem 1b)

Answer/Discussion to 1c

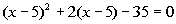
Step 1: Write in Standard Form, 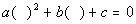, if needed.

This equation is already in standard form.

Step 2: Substitute a variable in for the expression that follows b in the second term.

Note how the original equation has the exact same expression in the two ( )'s and that the first ( ) is squared and the 2nd ( ) is to the one power. This equation is quadratic in form.