College Algebra
Tutorial 20: Equations that are Quadratic in Form
In this tutorial, I will be stepping you through how to
solve equations
that are quadratic in form. These types of equations ultimately
lead
us to a quadratic equation. So, you know what that means. As
mentioned in previous tutorials, a lot of times in math you use
previous
knowledge to help work the new concepts. The main thing you need
to know from your past that will help you work the types of problems in
this tutorial is how to solve quadratic equations. If you need a
review on solving quadratic equations, feel free to go to Tutorial
17: Quadratic Equations. Solving equations is a big
part of algebra. It is very important to be able to solve all
different kinds of equations because equations can be used to solve all
kinds of problems, and you want to make sure you are prepared for any
type
of problem that comes your way. I think that you are ready to
move forward. |
 Tutorial Tutorial
|
Quadratic in Form
An equation is quadratic in form when
it can be written
in this
standard form
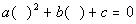
where the same expression is inside
both ( )'s.
|
In other words, if you have a times the
square of the expression following b plus b times that same expression not squared plus c equal to 0, you have an equation that is quadratic in form.
If we substitute what is in the ( ) with a
variable like t,
then the original equation will become a quadratic equation. |
Solving Equations that
are
Quadratic in Form
|
Step 1: Write
in Standard Form, 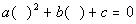 ,
if needed. ,
if needed.
If it is not in standard form, move any term(s)
to the appropriate
side by using the addition/subtraction property of equality.
Also, make sure that the squared term is written
first left to right,
the expression not squared is second and the constant is third and it
is
set equal to 0. |
Step 2: Substitute
a variable in for the expression that follows b in the second
term.
In other words, substitute your variable for what
is in the (
) when it is in standard form, 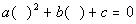 .
I’m going to use t for
my substitution,
but really you can use any variable as long as it is not the variable
that
is used in the original equation. |
Step 3: Solve the
quadratic equation created in step 2.
| You can use any method you want to solve the
quadratic equation: factoring,
completing the square or quadratic formula. |
Step 4: Find the
value of the variable from the original equation.
Keep in mind that you are finding a solution to
the original equation
and that the variable you substituted in for in step 2 is not your
original
variable.
Use the substitution that was used to set up step
2 and then solve for
the original variable. |
Step 5: Check
your solutions.
In some cases, you will be working with rational
exponents and square
roots in your problems. Those types of equations can cause
extraneous
solutions. Recall that an extraneous solution is one that is a
solution
to an equation after doing something like raising both sides of an
equation
by an even power, but is not a solution to the original problem. Even though not all of the quadratic in form
equations can cause extraneous
solutions, it is better to be safe than sorry and just check them all. |
|
Step 1: Write
in Standard Form, 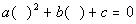 ,
if needed. ,
if needed. |
This equation is already in standard form. |
Below, I have the original equation rewritten in a way
to show you
that it is quadratic in form. Note how when you square y squared you get y to the fourth, which is
what
you have in the first term. |
|
*Rewriting original equation
to show it is
quadratic in form
*Note that (y squared) squared = y to the fourth
*When in stand. form, let t = the expression following b. |
Next, we need to substitute t in
for y squared in the original equation. |
|
*Original equation
*Substitute t in
for y squared |
Note how we ended up with a quadratic equation when we
did our substitution.
From here, we need to solve the quadratic equation that we have created. |
You can use any method you want to solve the quadratic
equation: factoring,
completing the square or quadratic formula.
I'm going to factor it to solve it. |
|
*Use Zero-Product Principle
*Set 1st factor = 0 and solve
*Set 2nd factor = 0 and solve
|
In step 2 we used the substitution of t = y squared. |
Let's find the value(s) of y when t = -4: |
|
*First solution
*Second solution
|
Let's find the value(s) of y when t = 1: |
|
*First solution
*Second solution
|
Step 5: Check
your solutions. |
Let's double check to see if y = 2i is a solution to the original equation. |
|
*Plugging in 2i for y
*i squared simplifies
to be -1
*i to
the fourth
simplifies to be 1
*True statement |
Since we got a true statement, y = 2i
is a solution. |
Let's double check to see if y = -2i is a solution to the original equation. |
|
*Plugging in -2i for y
*i squared simplifies
to be -1
*i to
the fourth
simplifies to be 1
*True statement |
Since we got a true statement, y = -2i
is a solution. |
Let's double check to see if y = 1 is
a solution to the original equation. |
|
*Plugging in 1 for y
*True statement |
Since we got a true statement, y = 1
is a solution. |
Let's double check to see if y = -1
is a solution to the original equation. |
|
*Plugging in -1 for y
*True statement |
Since we got a true statement, y = -1
is a solution. |
There are four solutions to this equation: y = 2i, y =
-2i, y = 1, and y = -1. |
Step 1: Write
in Standard Form, 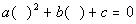 ,
if needed. ,
if needed. |
|
*Inverse of add. 3 is sub. 3
*Equation in standard form |
Below, I have the original equation rewritten in a way
to show you
that it is quadratic in form. Note how when you square x to the 1/3 power you get x to the 2/3
power,
which is what you have in the first term. |
|
*Rewriting original equation
to show it is
quadratic in form
*Note that (x to the 1/3 power) squared = x to the 2/3
power
*When in stand. form, let t = the expression following b. |
Next, we need to substitute t in
for x to
the 1/3 power in the original equation. |
|
*Original equation
*Substitute t in
for x to the 1/3 power |
Note how we ended up with a quadratic equation when we
did our substitution.
From here, we need to solve the quadratic equation that we have created. |
You can use any method you want to solve the quadratic
equation: factoring,
completing the square or quadratic formula.
I'm going to factor it to solve it. |
|
*Use Zero-Product Principle
*Set 1st factor = 0 and solve
*Set 2nd factor = 0 and solve
|
In step 2 we used the substitution of t = x to the 1/3 power. |
Let's find the value(s) of x when t = 3: |
|
*Inverse of taking it to the
1/3 power is
raising it to the 3rd power |
Let's find the value(s) of x when t = -1: |
|
*Inverse of taking it to the
1/3 power is raising it to the 3rd power |
Step 5: Check
your solutions. |
Let's double check to see if x = 27
is a solution to the original equation. |
|
*Plugging in 27 for x
*True statement |
Since we got a true statement, x = 27
is a solution. |
Let's double check to see if x = -1
is a solution to the original equation. |
|
*Plugging in -1 for x
*True statement |
Since we got a true statement, x = -1
is a solution. |
There are two solutions to this equation: x = 27 and x = -1. |
Step 1: Write
in Standard Form, 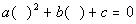 ,
if needed. ,
if needed. |
This equation is already in standard form. |
Note how the original equation has the exact same
expression in the
two ( )'s and that the first ( ) is squared and the 2nd
(
) is to the one power. This equation is quadratic in form. |
|
*When in stand. form, let t = the expression following b. |
Next, we need to substitute t in
for x squared plus 3x in the original
equation. |
|
*Original equation
*Substitute t in
for x squared plus 3x |
Note how we ended up with a quadratic equation when we
did our substitution.
From here, we need to solve the quadratic equation that we have created. |
You can use any method you want to solve the quadratic
equation: factoring,
completing the square or quadratic formula.
I'm going to factor it to solve it. |
|
*Use Zero-Product Principle
*Set 1st factor = 0 and solve
*2nd factor is the same as the 1st
|
In step 2 we used the substitution of t = x squared plus 3x. |
Let's find the value(s) of x when t = 4: |
|
*Use Zero-Product Principle
*Set 1st factor = 0 and solve
*First solution
*Set 2nd factor = 0 and solve
*Second solution |
Step 5: Check
your solutions. |
Let's double check to see if x = -4
is a solution to the original equation. |
|
*Plugging in -4 for x
*True statement |
Since we got a true statement, x = -4
is a solution. |
Let's double check to see if x = 1 is
a solution to the original equation. |
|
*Plugging in 1 for x
*True statement |
Since we got a true statement, x = 1
is a solution. |
There are two solutions to this equation: x = -4 and x = 1. |
 Practice Problems Practice Problems
These are practice problems to help bring you to the
next level.
It will allow you to check and see if you have an understanding of
these
types of problems. Math works just like
anything
else, if you want to get good at it, then you need to practice
it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the
problem out on
your own and then check your answer by clicking on the link for the
answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1c: Solve each quadratic in form equation. Practice
Problems 1a - 1c: Solve each quadratic in form equation.
 Need Extra Help on these Topics? Need Extra Help on these Topics?

WTAMU > Virtual Math Lab > College Algebra
Videos at this site were created and produced by Kim Seward and Virginia Williams Trice.
Last revised on Dec. 16, 2009 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward.
All rights reserved.
|
|


