College Algebra
Tutorial 12: Complex Numbers
 Learning Objectives
After completing this tutorial, you should be able to:
- Take the principle square root of a negative number.
- Write a complex number in standard form.
- Add and subtract complex numbers.
- Multiply complex numbers.
- Divide complex numbers.
|
Introduction
In this tutorial we will be looking at imaginary and
complex numbers.
Imaginary numbers allow us to take the square root of negative
numbers.
I will take you through adding, subtracting, multiplying and dividing
complex
numbers as well as finding the principle square root of negative
numbers.
I do believe that you are ready to get acquainted with imaginary and
complex
numbers. |
Tutorial
|
Imaginary Unit
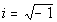where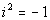 
|
This is the definition of an imaginary number.
From here on out, anytime that you have the square
root of -1 you
can simplify it as i and anytime you
have 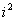 you can simplify it as -1. |
Standard Form
of
Complex Numbers
|
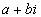
Complex numbers are made up of a real number part and
an imaginary
number part.
In this form, a is the
real number part and b is the imaginary number part.
Note that either one of these parts can be 0.
An example of a complex number written in standard
form is
 .
|
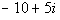Equality
of
Complex Numbers
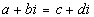
if and only if a = c AND b = d.
|
In other words, two complex numbers are equal to
each other if their
real numbers match AND their imaginary numbers match. |
Addition and Subtraction
of
Complex Numbers
|
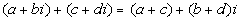
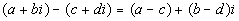
In other words, when you add or subtract two complex
numbers together,
you add or subtract the real number parts together, then add or
subtract
their imaginary parts together and write it as a complex number in
standard
form. |
|
*Add the real num. together and
the imaginary
num. together
*Complex num. in stand. form
|
|
*Subtract the real num. together
and the imaginary
num. together
*Complex num. in stand. form
|
Multiplying
Complex Numbers
|
Step 1: Multiply
the complex numbers in the same manner as polynomials. |
Step 2: Simplify
the expression. |
Add real numbers together and imaginary numbers
together.
Whenever you have an ,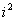
use the definition and replace it with -1. |
|
*Use dist. prop. to multiply
*i squared
= -1
|
|
*Complex num. in stand. form
|
|
*Use FOIL method to multiply
*Combine imaginary numbers
*i squared
= -1 |
|
*Complex num. in stand. form |
Step 1: Find
the conjugate of the denominator. |
You find the conjugate of a binomial by changing the
sign that is between
the two terms, but keep the same order of the terms.
a + bi and a - bi are conjugates of each other. |
Step 2: Multiply the numerator and the denominator of the fraction by the conjugate
found
in Step 1. |
Keep in mind that as long as you multiply the numerator
and denominator
by the exact same thing, the fractions will be equivalent.
When you multiply complex conjugates together you
get:
|
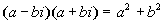
Step 3: Simplify
the expression. |
Add real numbers together and imaginary numbers
together.
Whenever you have an ,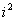
use the definition and replace it with -1. |
Step 1: Find
the conjugate of the denominator. |
In general the conjugate of a + bi is a - bi and
vice
versa.
So what would the conjugate of our denominator be?
It looks like the conjugate is  . |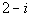
Step 2: Multiply the numerator and the denominator of the fraction by the conjugate
found
in Step 1
AND
Step 3: Simplify the expression. |
|
*Multiply top and bottom by
conj. of den.
*
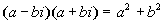
*i squared
= -1
|
|
*Divide each term of num. by 5
*Complex num. in stand. form
|
Step 1: Find
the conjugate of the denominator. |
In general the conjugate of a + bi is a - bi and
vice
versa.
So what would the conjugate of our denominator be?
It looks like the conjugate is  . |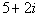
Step 2: Multiply the numerator and the denominator of the fraction by the conjugate
found
in Step 1
AND
Step 3: Simplify the expression. |
|
*Multiply top and bottom by
conj. of den.
*
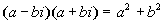
*i squared
= -1
|
|
*Divide each term of num. by 29
*Complex num. in stand. form |
Principal Square Root
of a Negative Number
For any positive real number b,
the principal
square root of the negative number, -b, is defined by
|
|
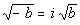
*Complex num. in stand. form
(note real num.
part is 0) |
Working problems with square roots of
negative numbers.
|
In other words use the definition of principal square
roots of negative
numbers before performing any operations. |
Step 2: Perform
the indicated operation. |
|
*Square root of a negative is i
|
Step 2: Perform
the indicated operation
AND
Step 3: Write
the final answer in standard form. |
|
*Rewrite 12 as (4)(3)
*The square root of 4 is 2
*Subtract like radicals: 2i- i = i
*Complex num. in stand. form (note
real num.
part is 0) |
|
*Square root of a negative is i
|
Step 2: Perform
the indicated operation
AND
Step 3: Write
the final answer in standard form. |
|
*i squared
= -1
*Complex num. in stand. form |
|
*Square root of a negative is i
|
Step 2: Perform
the indicated operation
AND
Step 3: Write
the final answer in standard form. |
|
*Rewrite 75 as (25)(3)
*The square root of 25 is 5
*Divide each term of num. by 5
*Complex num. in stand. form |
|
*Square root of a negative is i
|
Step 2: Perform
the indicated operation
AND
Step 3: Write
the final answer in standard form. |
|
*i squared
= -1
*Rewrite 60 as (4)(15)
*The square root of 4 is 2
*Complex num. in stand. form (note
that the
imaginary part is 0) |
Practice Problems
These are practice problems to help bring you to the
next level.
It will allow you to check and see if you have an understanding of
these
types of problems. Math works just like
anything
else, if you want to get good at it, then you need to practice
it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the
problem out on
your own and then check your answer by clicking on the link for the
answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1i: Perform the indicated operation. Write the answer in standard form.
Need Extra Help on these Topics?
Videos at this site were created and produced by Kim Seward and Virginia Williams Trice.
Last revised on Dec. 15, 2009 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward.
All rights reserved.
|
|
Example
1: Add 
.
.
.
.
.
.
.
