Intermediate Algebra
Answer/Discussion to Practice Problems
Tutorial 4: Operations on Numbers
 Answer/Discussion
to 1a
-5 + (-16)
-5 + (-16) = -21.
Note that we are adding two numbers with the same sign. The sum
of the absolute values 5 and 16 is 21 and their common sign is negative. Therefore,
our answer is -21.
(return
to problem 1a) |
Answer/Discussion
to 1b
7 + (-3)
7 + (-3) = 4.
Note that we are adding two numbers that have opposite signs.
The difference between the absolute values of 7 and 3 is 4 and the sign
of the number with the larger absolute value (7) is positive. Therefore,
our answer is 4.
(return
to problem 1b) |
Answer/Discussion
to 1c
-10 - (-2)
-10 - (-2) = -10 + 2 = -8.
Subtracting a negative 2 is the same as adding a positive 2. Once
we change it to addition, we now are adding two numbers with opposite signs.
The difference of the absolute values of 10 and 2 is 8 and the sign of
the larger absolute value (-10) is negative. Therefore, our answer
is -8.
(return
to problem 1c) |
Answer/Discussion
to 2a
(-4)(9)
(-4)(9) = -36.
We are multiplying two numbers with opposite signs. The product
of 4 and 9 is 36 and multiplying with opposite signs gives us a negative. Therefore,
our answer is -36.
(return
to problem 2a) |
Answer/Discussion
to 2b
= .5 or ½.
We are dividing two numbers with the same sign. The quotient of
3 and 6 is .5 and dividing with the same signs gives us a positive number. Therefore,
our answer is .5.
(return
to problem 2b) |
Answer/Discussion
to 3a
|
|
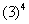
*Write the base 3 in a product 4 times
*Multiply
|
Answer/Discussion
to 3b
|
|
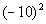
*Write the base -10 in a product 2 times
*Multiply
|
Answer/Discussion
to 3c
|
|
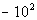
*Negate 10 squared
*Put a - in front of 10 written in a product
2 times
*Multiply |
Answer/Discussion
to 4a
The thought behind this is that we are looking for the square root of
36, which means we are looking for a number that when we square it we get
36. Since 6 squared is 36, 6 is the square root of 36.
Note that we are only interested in the principal root and since 36 is
positive and there is not a sign in front of the radical, our answer is
positive 6. If there had been a negative in front of the radical
our answer would have been -6
(return
to problem 4a) |
Answer/Discussion
to 4b
Now we are looking for the fourth root of 1/16, which means we are looking
for a number that when we take it to the 4th power, we get 1/16.
Since 1/2 to the 4th power is 1/16, our answer is going to be 1/2.
(return
to problem 4b) |
Answer/Discussion
to 5a
|
|
*( )
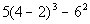
*Exponents
*Multiplication
*Subtraction
|
Answer/Discussion
to 5b
|
|
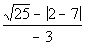
*Absolute value
*(fancy grouping symbol)
*Square root
*Subtraction in numerator
*Divide
|
Answer/Discussion
to 6a
Find the value of the expression when a = 3 and b = -2.
 |
|
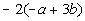*Replace a with
3 and b with -2
*Multiply within ( )
*Subtract within ( )
*Multiply
|
Last revised on June 10, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward.
All rights reserved.
|
|
