Intermediate Algebra
Answer/Discussion to Practice Problems
Tutorial 3: Sets of Numbers
 Answer/Discussion
to 1a
{x | x is a
natural number less than 4}
There are two parts to this:
- the number has to belong to the set of natural numbers {1, 2, 3, 4, ...}
and
- it has to be less than 4.
Putting these two ideas together we get
{1, 2, 3}
(return to problem
1a) |
Answer/Discussion
to 1b
{x | x is
a whole number between 100 and 105}
There are two parts to this:
- the number has to belong to the set of whole numbers {0, 1, 2, 3, 4, ...}
and
- it has to be between 100 and 105, not including 100 and 105.
Putting these two ideas together we get
{101, 102, 103, 104}
(return to problem
1b) |
Answer/Discussion
to 1c
{x | x is an
odd whole number greater than 5}
There are three parts to this:
- the number has to belong to the set of whole numbers {0, 1, 2, 3, 4, ...}
and
- it has to be greater than 5 and
- it has to be odd.
Putting these two ideas together we get
{7, 9, 11, 13 ...}
(return to problem
1c) |
Answer/Discussion
to 2a
{-3, -3/2, 0, .25, 1}
Note that we have two non-integer numbers to graph. The -3/2 will
go halfway between -2 and -1. The .25 will go between 0 and 1, a
little closer to 0 than 1.
(return to problem
2a) |
Answer/Discussion
to 3a
Natural numbers
The numbers in the given set that are also natural numbers are
{2,  }.
Note that simplifies to be 3 which is a natural number.
(return to
problem 3a) |
Answer/Discussion
to 4a
0 ? {x | x is
a rational number}
Since 0 can be written as 0/1 (one integer over another), it is a part
of the list of rational numbers. So it would be true to say
0  {x | x is a rational number}.
(return to problem
4a) |
Answer/Discussion
to 4b
10 ? { 2, 4, 6, 8, ...}
The ellipsis in the set indicate that the pattern of numbers (even natural
numbers) would continue, which means 10 would be included in this list.
So it would be true to say
10
{2, 4, 6, 8, ...}.
(return to problem
4b) |
Answer/Discussion
to 4c
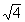 ? {x | x is an irrational number}
Since 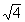simplifies
to be 2, which is a rational number, it can not be an irrational number.
Therefore,
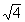 {x | x is an irrational number}.
(return to problem
4c) |
Answer/Discussion
to 6a
|10|
When looking for the absolute value of 10, we are looking for the number
of units (or distance) 10 is from 0 on the number line.
I came up with 10, how about you?
(return to problem
6a) |
Answer/Discussion
to 6b
- |-10|
This problem has a little twist to it. Let's talk it through.
First of all, if we just concentrate on |-10| we would get 10.
Then, note that there is a negative on the OUTSIDE of the absolute value.
That means we are going to negate what we get for the absolute value.
Putting that together we get -10 for our answer.
Note that the absolute value part of the problem was still positive.
We just had a negative on the outside of it that made the final answer
negative.
(return to problem
6b) |
Answer/Discussion
to 7a
½
The opposite of 1/2 is -1/2, since both of these numbers have
the same absolute value but are on opposite sides of the origin on the
number line.
(return to problem
7a) |
Answer/Discussion
to 7b
-20
The opposite of -20 is 20, since both of these numbers have the
same absolute value but are on opposite sides of the origin on the number
line.
(return to problem
7b) |
Last revised on June 10, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward.
All rights reserved.
|
|
}.
R