---

Problem 1a:

 

1a.  Answer:

 

Step 1: Graph the first equation.

 

x-intercept

 
 

The x-intercept is (4, 0).   y-intercept

 
 

The y-intercept is (0, -2).   Find another solution by letting x = 1

 
 

Another solution is (1, -3/2).   Solutions:    x y (x, y) 4 0 (4, 0) 0 -2 (0, -2) 1 -3/2 (1, -3/2)   Plotting the ordered pair solutions and drawing the line:

 

Step 2: Graph the second equation on the same coordinate system as the first.

 
 

x-intercept

 
 

The x-intercept is (-1/2, 0).   y-intercept

 
 

The y-intercept is (0, 1).   Find another solution by letting x = 1.

 
 

Another solution is (1, 3).   Solutions:   x y (x, y) -1/2 0 (-1/2, 0) 0 1 (0, 1) 1 3 (1, 3) Plotting the ordered pair solutions and drawing the line:

 

Step 3: Find the solution.

 

We need to ask ourselves, is there any place that the two lines intersect, and if so, where? The answer is yes, they intersect at (-2, -3).

 

Step 4: Check the proposed ordered pair solution in BOTH equations.

 

You will find that if you plug the ordered pair (-2, -3) into BOTH equations of the original system,  this is a solution to BOTH of them.   The solution to this system is (-2, -3).

 
 
 

Problem 2a:

 

2a.  Answer:

 

Step 1: Simplify if needed.

 

Both of these equations are already simplified.  No work needs to be done here.

 

Step 2:  Solve one equation for either variable.

 

It does not matter which equation or which variable you choose to solve for.  But it is to your advantage to keep it as simple as possible.  Second equation solved for y:

 
 

Step 3: Substitute what you get for step 2 into the other equation  AND Step 4:  Solve for the remaining variable .

 

Substitute the expression  -10 + 6x for y into  the first equation and solve for x: (when you plug in an expression like this, it is just like you plug in a number for your variable)

 
 

Step 5:  Solve for second variable.

 

Plug in 4/3 for x into the equation in step 2 to find y's value.

 
 

Step 6: Check the proposed ordered pair solution in BOTH original equations.

 

You will find that if you plug the ordered pair (4/3, -2) into BOTH equations of the original system, that this is a solution to BOTH of them. (4/3, -2) is a solution to our system.

 
 
 

Problem 3a:

 

3a.  Answer:

 
 

Step 1: Simplify and put both equations in the form Ax + By = C if needed.

 

Multiplying each equation by it's respective LCD we get:

 
 

Step 2: Multiply one or both equations by a number that will create opposite coefficients for either x or y if needed AND Step 3: Add equations

 

I propose that we multiply the first equation by 2, this would create a 4 in front of x and we will have our opposites.   Multiplying the first equation by 2 we get:

 
 

Step 4: Solve for remaining variable.

 

Since both variables dropped out AND we have a FALSE statement, then our answer is no solution.

 

Step 5: Solve for second variable.

 

No variable to plug in here.

 

Step 6: Check the proposed ordered pair solution in BOTH original equations.

 

The answer is no solution.

 
 
 

Problem 4a:

 

4a.  Answer:

 

Note that the numbers in (  ) are equation numbers.  They will be used throughout the problems for reference purposes.

 

Step 1: Simplify and put both equations in the form Ax + By + Cz = D if needed.

 

No simplification needed here.  Let's go on to the next step.

 
 

Step 2: Choose to eliminate any one of the variables from any pair of equations.

 

I choose to eliminate y. Since z is already eliminated from the first equation we will use that first equation in it's original form for this step:

 
 
 

Step 3:  Eliminate the SAME variable chosen in step 2 from any other pair of equations creating a system of two equations and 2 unknowns.

 

We are still going after eliminating z, this time I want to use the second and the third equations.  Multiplying the third equation by -1 and adding this to the first equation we get:

 
 
 
 

Step 4:  Solve the remaining system found in step 2 and 3.

 

Let's first put those equations together:

 
 

I'm going to choose x to eliminate.  Multiplying equation (2) by 3 and equation (4) by -2 and then adding them together we get:

 
 

Solving for z we get:

 
 

If we go back one step to the system that had two equations and two variables and plug in 1 for z in equation (2), we  would get:

 
 
 

Step 5:  Solve for the third variable.

 

Now we need to go back to the original system and pick any equation to plug in the two known variables and solve for our last variable .  I choose equation (1) to plug in 1 for x that we found:

 
 
 

Step 6:  Check.

 

You will find that if you plug the ordered triple (1, 3, 1) into ALL THREE equations of the original system, this is a solution to ALL THREE of them. (1, 3, 1) is a solution to our system.

 
 
 
 

Problem 5a:

 

5a.   A boat on a river travels 20 miles downstream in only 2 hours.  It takes the same boat 6 hours to travel 12 miles upstream.  What are the speed of the boat and the speed of the current? Answer:

 
 

Step 1:  Understand the problem.

 

Make sure that you read the question carefully several times.  Since we are looking for two different rates, we will let  x = rate of the boat y = the rate of the current Keep in mind that the current is affecting the overall speed.  When the boat is going downstream, it will be going faster.  That rate will be x + y.  When the boat is going upstream, it will be going slower.  That rate will be x - y.       (Rate) (Time) =  Distance Downstream x + y 2 20 Upstream x - y 6 12

 
 

Step 2:  Devise a plan (translate).

 

Since we have two unknowns, we need to build a system with two equations. Equation (1): Equation (2):

 

Putting the two equations together in a system we get:

 
 

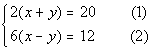
Step 3:  Carry out the plan (solve).

 

Simplify if needed. We can simplify this by dividing both sides of equation (1) by 2 and equation (2) by 6 getting rid of the ( ):

 
 

Multiply one or both equations by a number that will create opposite coefficients for either x or y if needed AND add the equations. Since we already have opposite coefficients on y, we can go right into adding equations (3) and (4) together:

 
 

Solve for remaining variable. Solving for x we get:

 
 

Solve for second variable. Using equation (3) to plug in 6 for x and solving for y we get:

 
 
 

Step 4:  Look back (check and interpret).

 

You will find that if you plug the ordered pair (6, 4) into BOTH equations of the original system, this is a solution to BOTH of  them.  Final Answer: The boat speed is 6 mph and the current speed is 4 mph.

 
 
 

Problem 5b:

 

5b. The sum of three numbers is 8.  Twice the smallest is 2 less than the largest, while the sum of the largest and the smallest is 5.   What are the three numbers? Answer:

 
 

Step 1:  Understand the problem.

 

Make sure that you read the question carefully several times.  Since we are looking for three numbers, we will let    x = the smallest number y = middle number z = the largest number

 
 

Step 2: Devise a plan (translate).

 

Since we have three unknowns, we need to build a system with three equations. Equation (1): Equation (2): Equation (3):

 

Putting the three equations together in a system we get:

 
 

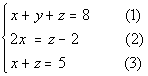
Step 3:  Carry out the plan (solve).

 

Simplify and put all three equations in the form Ax + By  + Cz = D if needed. Equation (2) needs to be put in the correct form:

 
 

Choose to eliminate any one of the variables from any  pair of equations. Since y is already eliminated in equation (4) and (3), it would be quickest and easiest to eliminate y. We can use equation (4) as one equation with y eliminated:

 
 

Eliminate the SAME variable chosen in step 2 from any other pair of equations creating a system of two equations and 2 unknowns.   We can use equation (3) as another equation with y eliminated:

 
 

Solve the remaining system found in the above steps Putting those two equations together we get:

 
 

Solving for x we get:

 
 

Using equation (4) to plug in 1 for x and solving for z we get:

 
 

Solve for the third variable. Using equation (1) to plug 1 in for x and 4 for z and solving for y  we get:

 
 
 

Step 4:  Look back (check and interpret).

 

You will find that if you plug the ordered triple (1, 3, 4) into ALL THREE equations of the original system, this is a solution to ALL THREE of  them.    Final Answer: 1 is the smallest number, 3 is the middle number and 4 is the largest number.

 

---

Last revised on July 6, 2011 by Kim Seward.
All contents copyright (C) 2001 - 2011, WTAMU and Kim Seward. All rights reserved.