Answer:

(2, -4) lies in Quadrant IV.

Answer:

(0, 4) lies on the y-axis.

2a. 

Answer:

Since we can write it in the standard form Ax + By = C, then we have a linear equation. 

This means that we will have a line when we go to graph this. 

Solutions:
 

x		(x, y)
-1	y = 3(-1) - 4 = -7	(-1, -7)
0	y = 3(0) - 4 = - 4	(0, - 4)
1	y = 3(1) - 4 = -1	(1, -1)

2b. 

Answer:

It looks like we cannot write it in the form Ax + By = C because the x has to be to the one power, not squared.  So this is not a linear equation. 

Solutions:
 

x		(x, y)
-3	y = (-3)^2 - 7 = 2	(-3, 2)
-2	y = (-2)^2 - 7 = -3	(-2, -3)
-1	y = (-1)^2 - 7 = -6	(-1, -6)
0	y = (0)^2 - 7 = -7	(0, -7)
1	y = (1)^2 - 7 = -6	(1, -6)
2	y = (2)^2 - 7 = -3	(2, -3)
3	y = (3)^2 - 7 = 2	(3, 2)

Answer:

If you got {-1, -2, -3}, you are correct!
 
 

Range
We need to find the set of all output values.  In terms of ordered pairs, that correlates with the second component of each one.  So, what do you get for the range?

If you got {3, 4, 5, 6}, you are absolutely right!
 
 

Is this a function or not?
We need to ask ourselves, does every first element (or input) correspond with EXACTLY ONE second element (or output)?  In this case, the answer is no.  -1 associates with two values, 3 and 4.

So, this relation would not be an example of a function.

Answer:

Since that is the case, we need to look to the left and right and see if there are any end points.  In this case, note how the line has arrows at both ends, that means it would go on and on forever to the right and to the left. 

This means that the domain is {x | x is a real number}.
 
 

Range
We need to find the set of all output values.  In terms of ordered pairs, that correlates with the second component of each one. In terms of this two dimensional graph, that corresponds with the y values (vertical axis). 

Since that is the case, we need to look up and down and see if there are any end points.  In this case, note how the line has arrows at both ends, that means it would go on and on forever up and down. 

This means that the range is {y | y is a real number}.
 
 

Vertical Line Test
This graph would pass the vertical line test, because there would not be any place on it that we could draw a vertical line and it would intersect it in more than one place.
 

Therefore, this is a graph of a function.

Answer:

Since that is the case, we need to look to the left and right and see if there are any end points.  In this case, note that the farthest left point is (-6, 0) and it keeps going and going to the right.   That means that if we wrote out ordered pairs for all the values, we would use the values greater than or equal to -6 for x.

This means that the domain is {x | x>  -6}.
 

Range
We need to find the set of all output values.  In terms of ordered pairs, that correlates with the second component of each one. In terms of this two dimensional graph, that corresponds with the y values (vertical axis). 

Since that is the case, we need to look up and down and see if there are any end points.   In this case, note how the curve has arrows at both ends, that means it would go on and on forever up and down. 
 

This means that the range is {y | y is a real number}.
 
 

Vertical Line Test
This graph would not pass the vertical line test, because there is at least one place on it that we could draw a vertical line and intersect it in more than one place.  In fact, there a lot of vertical lines that we can draw that would intersect it in more than one place, but we only need to show one to say it is not a function.

The graph below shows one vertical line drawn through our graph that intersects it in two places.

Therefore, this is not a graph of a function.

5a. 

Answer:

If you answered yes, you are right on. 

Note that since it is solved for y, y is our output value and x is our input value. 

Since our answer to that question is yes, that means by definition, y is a function of x.

6a. 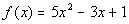  ;  f(0), f(1), f(-1)

Answer:

*Plug in 1 for x and evaluate
 
 
 
 
 
 

*Plug in -1 for x and evaluate
 

6b. 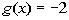;   g(0), g(½),  g(5)

Answer:

*This is a constant function that is always -2
 
 
 
 

*This is a constant function that is always -2

7a. 

Answer:

Let's first find the x-intercept. 

*Inverse of mult. by 2 is div. by 2
 

Next we will find the y-intercept.

*Inverse of mult. by -1 is div. by -1

We can plug in any x value we want as long as we get the right corresponding y value and the function exists there. 

Let's put in an easy number  x = 1:

*Inverse of add 2 is sub. 2
 

*Inverse of mult. by -1 is div. by -1

Note that we could have plugged in any value for x: 5, 10, -25, ...,  but it is best to keep it as simple as possible.
 

Solutions:
 

7b. 

Answer:

Let's first find the x-intercept.

*Inverse of mult. by 4 is div. by 4

Since the x-intercept came out to be (0, 0), then it stands to reason that when we put  in 0 for x to find the y-intercept we will get (0, 0). 

Since we really have found only one point, this time we better find two additional solutions so we have a total of three points.

We can plug in any x value we want as long as we get the right corresponding y value and the function exists there. 

Let's put in an easy number x = 1:

Let's put in another easy number x = -1:

Note that we could have plugged in any value for x: 5, 10, -25, ...,  but it is best to keep it as simple as possible.
 

Solutions:
 

8a. 

Answer:

Since this is a special type of line, I thought I would talk about steps 1 and 2 together.

It doesn't matter what x is, y is always - 4.  So for our solutions we just need three ordered pairs such that y = - 4. 

Note that the y-intercept (where x = 0) is at (0, - 4). 

Do we have an x-intercept? The answer is no.  Since y has to be - 4, then it can never equal 0, which is the criteria of an x-intercept.  Also, think about it, if we have a horizontal line that crosses the y-axis at - 4, it will never ever cross the x-axis.

So some points that we can use are (0, - 4), (1, - 4) and (-1, - 4).  These are all ordered pairs that fit the criteria of y having to be 4.

Of course, we could have used other solutions, there are an infinite number of them.
 

Solutions:
 

Answer:

*Simplify
 

Answer:

*Simplify
 

10a. 

Answer:

*Inverse of mult. by -3 is div. by -3
 

*Slope/intercept form of the line

I got m = 2/3 and y-intercept is -2.

10b. 

Answer:

This linear equation is already in the slope/intercept form.

Note how we are missing a constant being added to the x term.  If we are missing that constant, what is it understood to be???

The slope is -2 and the y-intercept is 0.

Answer:

Let's find that slope:

*Plug in values 

*Simplify
 

We want to put the slope and one point into the point/slope equation.

*Inverse of sub. 3 is add 3
*Slope/intercept form of the line
*Function notation

11b.   Passes through the point (1, 1) and is parallel to the line 

Answer:

Find the slope of the parallel line:

OK, now we have our slope, which is 1/2. 

We want to put the slope and one point into the point/slope equation.

*Inverse of sub. 1 is add 1
 
 

*Slope/intercept form of the line
 

*Function notation

11c.  Passes through the point (-2, 3) and is perpendicular to the line 

Answer:

Find the slope of the perpendicular line:

*Inverse of mult. by 3 is div. by 3

*Slope/intercept form of the line

What did you come up with? 
I came up with 3 for the slope of our line. 

Now we can go on to the equation of our line:

*Slope/intercept form of the line
*Function notation

Answer:

Since it passes through (-3, 2), and a vertical line is in the form x = c, where the x value is ALWAYS equal to the same value throughout, this means our equation would have to be x = -3.

Note that -3 is the x value of the ordered pair given.

13a. 

Answer:

When I'm working with only the boundary line, I will put an equal sign between the two sides to emphasize that we are working on the boundary line.  That doesn't mean that I changed the problem. When we put it all together in the end, I will put the inequality back in.

x-intercept:

*Inverse of mult. by 2 is div. by 2

*x-intercept

y-intercept

*Inverse of mult. by -2 is div. by -2

*y-intercept

Plug in 1 for x to get a third solution:

*Inverse of add 2 is sub. 2
 

*Inverse of mult. by -2 is div. by -2

Solutions:
 

Since the original problem has a <, this means it DOES NOT include the boundary line. 

So are we going to draw a solid or a dashed line for this problem? 
It looks like it will have to be a dashed line.

Putting it all together, we get the following boundary line for this problem:

An easy test point would be (0, 0).  Note that it is a point that is not on the boundary line. In fact, it is located above the boundary line. 

Let's put (0, 0) into the original problem and see what happens:

Our solution would lie above the boundary line.  This means we will shade in the part that is above it.

Note that the gray lines indicate where you would shade your final answer.

14a.    OR 

Answer:

Graph the First Inequality 

Step 1:  Graph the boundary line.

Do you remember what type of line y = c graphs as?
It comes out to be a horizontal line. 

Every y's value on the boundary line would have to be 4. 

Solutions:
 

So are we going to draw a solid or a dashed line for this problem? 
It looks like it will have to be a solid line.

Putting it all together, we get the following boundary line for this problem:

An easy test point would be (0, 0).  Note that it is a point that is not on the boundary line. In fact, it is located below the boundary line. 

Let's put (0, 0) into the original problem and see what happens:

Our solution would lie below the boundary line.  This means we will shade in the part that is below it.

Note that the gray lines indicate where you would shade your final answer.

Graph the Second Inequality 

Step 1:  Graph the boundary line.

Do you remember what type of line x = c graphs as?
It comes out to be a vertical line. 

Every x's value on the boundary line would have to be 1. 

Solutions:
 

So are we going to draw a solid or a dashed line for this problem? 
It looks like it will have to be a dashed line.

Putting it all together, we get the following boundary line for this problem:

An easy test point would be (0, 0).  Note that it is a point that is not on the boundary line. In fact, it is located to the left of the boundary line. 

Let's put (0, 0) into the original problem and see what happens:

Our solution would lie to the right of the boundary line.  This means we will shade in the part that is to the right of it

Note that the gray lines indicate where you would shade your final answer.

This is what we get when we union these two inequalities:

Note that the gray lines indicate where you would shade your final answer.

14b.   AND 

Answer:

Graph the First Inequality 

Step 1:  Graph the boundary line.

Do you remember what type of line x = c graphs as?
It comes out to be a vertical line. 
 

Every x's value on the boundary line would have to be -2. 

Solutions:
 

So are we going to draw a solid or a dashed line for this problem? 
It looks like it will have to be a dashed line.

Putting it all together, we get the following boundary line for this problem:

An easy test point would be (0, 0).  Note that it is a point that is not on the boundary line. In fact, it is located to the right of the boundary line. 

Let's put (0, 0) into the original problem and see what happens:

Our solution would lie to the left of the boundary line.  This means we will shade in the part that is to the left of it

Note that the gray lines indicate where you would shade your final answer.

Graph the Second Inequality 

Step 1:  Graph the boundary line.

Do you remember what type of line y = c graphs as?
It comes out to be a horizontal line. 
 

Every y's value on the boundary line would have to be -2. 

Solutions:
 

So are we going to draw a solid or a dashed line for this problem? 
It looks like it will have to be a solid line.

Putting it all together, we get the following boundary line for this problem:

An easy test point would be (0, 0).  Note that it is a point that is not on the boundary line. In fact, it is located above the boundary line.

Let's put (0, 0) into the original problem and see what happens:

Our solution would lie above the boundary line.  This means we will shade in the part that is above it

Note that the gray lines indicate where you would shade your final answer.

This is what we get when we intersect these two inequalities:

Note that the gray lines indicate where you would shade your final answer.