College Algebra
Answer/Discussion to Practice Problems
Tutorial 7: Factoring Polynomials
 Answer/Discussion
to 1a
|
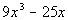
The first thing that we always check when we are factoring is WHAT?
The GCF. In this case, there is one.
Factoring out the GCF of x we get: |
|
*Factor an x out
of every term
|
Next, we assess to see if there is anything else that we can factor.
This fits the form of the difference
of two squares. So we will factor using that rule: |
|
*Fits the form of a diff. of two squares
*Factor as the prod. of sum and diff. of bases
|
Note that if we would multiply this out and the original expression
out we would get the same polynomial. |
Answer/Discussion
to 1b
|
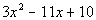
The first thing that we always check when we are factoring is WHAT?
The GCF. In this case, there is not one.
So we assess what we have. This is a trinomial that does not fit the
form of a perfect square trinomial. Looks like we will have to use trial
and error: |
|
*Factor by trial and error
|
There is no more factoring that we can do in this problem.
Note that if we would multiply this out, we would get the original polynomial. |
Answer/Discussion
to 1c
|
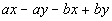
The first thing that we always check when we are factoring is WHAT?
The GCF. In this case, there is not one.
So we assess what we have. This is a polynomial with four terms.
Looks like we will have to try factoring
it by grouping: |
|
*Group in two's
*Factor out the GCF out of each separate (
)
*Factor out the GCF of (x
- y)
|
There is no more factoring that we can do in this problem.
Note that if we would multiply this out, we would get the original polynomial. |
Answer/Discussion
to 1d
|
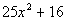
Since this is a SUM of two squares it DOES NOT factor.
That means this polynomial is prime. |
Answer/Discussion
to 1e
|
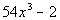
The first thing that we always check when we are factoring is WHAT?
The GCF. In this case, there is one.
Factoring out the GCF of x we get: |
|
*Factor a 2 out
of every term
|
Next, we assess to see if there is anything else that we can factor.
This fits the form of the difference
of two cubes. So we will factor using that rule: |
|
*Fits the form of a diff. of two cubes
*Binomial is diff. of bases
*Trinomial is 1st base squared, plus prod.
of bases, plus 2nd base squared |
There is no more factoring that we can do in this problem.
Note that if we would multiply this out, we would get the original polynomial. |
Answer/Discussion
to 1f
|
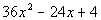
The first thing that we always check when we are factoring is WHAT?
The GCF. In this case, there is one.
Factoring out the GCF of x we get: |
|
*Factor a 4 out
of every term
|
Next, we assess to see if there is anything else that we can factor.
This fits the form of the perfect
square trinomial. So we will factor using that rule: |
|
*Fits the form of a perfect sq. trinomial
*Factor as the diff. of bases squared |
There is no more factoring that we can do in this problem.
Note that if we would multiply this out, we would get the original polynomial. |
Last revised on Dec. 13, 2009 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.
|
|
