College Algebra
Answer/Discussion to Practice Problems
Tutorial 59: Practice Test on Tutorials 54A - 58
Problem 1a: Write a formula for the nth term of the
infinite
sequence. Do not use a recursion formula. |
Problem 2a: Find the first four terms and the 10th
term of
the arithmetic sequence. |
Problem 3a: Find the first four terms AND the common
ratio of
the geometric sequence.
|
3a. 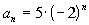
 Answer: Answer:

The common ratio is -2.
|
|
Problem 4a: Write the geometric series in summation
notation. |
Problem 5a: Find the sum of the arithmetic series. |
Problem 6a: Find the sum of the infinite geometric
series. |
Problem 7a: Evaluate the given binomial coefficient. |
Problem 8a: Use the Binomial Theorem to expand
the
binomial
and express the result in simplified form. |
Problem 9a: Find the term indicated in the
expansion. |
Problems 10a - 10f: Solve by the method of
your choice. |
10a. Next semester you are going to take one
business
class, one math class, one political science class one english class
and one fine arts class. According to the schedule you have 3
different business classes, 5 different math classes, 1 political
science class, 4 different English classes, and 2 Fine Arts classes to
choose from. Assuming no scheduling conflicts, how many different
five-course selections can you make?
 Answer: Answer:

|
|
10b. In how many ways can 8 employees be assigned
to 8
different jobs?
 Answer: Answer:

|
|
10c. A computer password can use any letter of
the
alphabet, and a sequence of 5 different letters must be selected for
the password. How many computer passwords are possible?
 Answer: Answer:

|
|
10d. A boss has 8 employees and 5 are
chosen to
give a
presentation. How many different ways can the boss choose the
presenters if the order of the presenters is important?
 Answer: Answer:

|
|
10e. A boss has 8 employees and 5 are chosen to
give a
presentation. How many different ways can the boss choose the
presenters if the order of the presenters is not important?
 Answer: Answer:

|
|
10f. 15 students of whom 9 are seniors, 4 are
juniors,
and 2 are sophomores, are selected as semi-finalists for a literary
award. Of the 15 students, 5 finalists will be selected.
1) In how many ways can 5 finalists be
selected
from the 15 students?
 Answer: Answer:

|
2) In how many ways can the 5 finalists
contain
only seniors?
 Answer: Answer:

|
3) In how many ways can the 5 finalist
contain
exactly 1 sophomore and 4 juniors?
 Answer: Answer:

|
|
|
Problems 11a - 11b: 200 college students took
a survey on their
favorite soda pop. The results are as follows: 125 said their
favorite was Coke. 25 said their favorite is Diet Coke. 30
said their favorite is Dr. Pepper. 15 said their favorite was
Sprite. And 5 said their favorite was Mountain Dew.
If each student picked only one favorite, find the
following
probabilities. |
11a. A student's favorite soda pop is Diet Coke.
 Answer: Answer:

|
11b. A student’s favorite soda pop is Sprite.
 Answer: Answer:

|
|
Problems 12a - 12b: From a group of 7
seniors and 9
juniors, 4 people are selected at random to form a committee.
Find the probability that |
12a. Only seniors are selected.
 Answer: Answer:

|
|
12b. Exactly 2 seniors and 2 juniors are selected.
 Answer: Answer:

|
|
Problems 13a - 13c: An employee’s name will be
picked at random
to go on a business trip with the boss. There are 20 senior level
executives, 15 junior level executives, 18 senior level programmers, 12
junior level programmers, 5 senior level assistants and 5 junior level
assistants.
Find the probability that |
13a. a programmer OR an assistant will be picked.
 Answer: Answer:
Mutually exclusive:

|
|
13b. a senior level employee OR an executive will
be
picked.
 Answer: Answer:
Not mutually exclusive:

|
|
13c. a junior level employee will not be picked.
 Answer: Answer:

|
|
Problem 14a: Find the probability. |
14a. If 1 card is drawn from a deck of
cards and
1 die
is rolled find the probability that the card drawn is a diamond AND the
number rolled on the die is even.
 Answer: Answer:
Sets are independent of each other:

|
|

Last revised on May 21, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward.
All rights reserved.
|
|


