College Algebra
Answer/Discussion to Practice Problems
Tutorial 58: Probability
 Answer/Discussion
to 1a Answer/Discussion
to 1a
Find the probability that a student's favorite type of music is jazz.
Round answer to three decimal places. |
To find this probability, we need to know n(E)
= n(students whose favorite type of music is jazz), which is the number
of students who preferred jazz and n(S) = n(students
surveyed), which is the total number of students surveyed.
What do you think n(E) = n(students
whose favorite type of music is jazz) is?
If you said 24 you are correct. 24 students indicated that their
favorite type of music is jazz.
What do you think n(S) = n(students
surveyed) is?
If you said 128 give yourself a pat on the back. If you total
51 + 24 + 33 + 5 + 15 you get 128.
Putting this together in the Empirical Probability formula you get: |
|
*putting in the numbers found above
*reducing the fraction
*rounding to 3 decimal places |
The probability that a student's favorite
type of music is jazz is .188. |
 Answer/Discussion
to 1b Answer/Discussion
to 1b
Find the probability that a student's favorite type of music is classical.
Round answer to three decimal places. |
To find this probability, we need to know n(E)
= n(students whose favorite type of music is classical), which is the number
of students who preferred classical and n(S)
= n(students surveyed), which is the total number of students surveyed.
What do you think n(E) = n(students
whose favorite type of music is classical) is?
If you said 5 you are correct. 5 students indicated that their
favorite type of music is classical.
What do you think n(S) = n(students
surveyed) is?
If you said 128 give yourself a pat on the back. If you total
51 + 24 + 33 + 5 + 15 you get 128.
Putting this together in the Empirical Probability formula you get: |
|
*putting in the numbers found above
*rounding to 3 decimal places |
The probability that a student's favorite
type of music is classical is .039. |
 Answer/Discussion
to 2a Answer/Discussion
to 2a
Find the probability that you are dealt a jack. Round answer to
three decimal places. |
To find this probability we need to know n(E)
= n(jacks), which is the number of jacks in a deck of cards and n(S)
= n(cards in a deck), which is the total number of cards in a deck.
What do you think n(E)
= n(jacks) is?
If you said 4 you are correct. There are 4 jacks in a deck of
cards.
What do you think n(S)
= n(cards in a deck) is?
If you said 52 give yourself a pat on the back. There are 52 cards
in a deck.
Putting this together in the Theoretical Probability formula you
get: |
|
*putting in the numbers found above
*reducing the fraction
*rounding to 3 decimal places |
The probability that a jack is dealt is .077. |
 Answer/Discussion
to 2b Answer/Discussion
to 2b
Find the probability that you are dealt a heart or club. Round
answer to three decimal places. |
|
Let's break it down first by finding each separate probability.
P(a heart is dealt)
To find this probability we need to know n(E)
= n(hearts), which is the number of hearts in a deck of cards and n(S)
= n(cards in a deck), which is the total number of cards in a deck.
What do you think n(E)
= n(hearts) is?
If you said 13 you are correct. There are 13 hearts in a deck
of cards.
What do you think n(S)
= n(cards in a deck) is?
If you said 52 give yourself a pat on the back. There are 52 cards
in a deck.
Putting this together in the Theoretical Probability formula you
get: |
|
*putting in the numbers found above
*reducing the fraction
*rounding to 3 decimal places |
P(a club is dealt)
To find this probability we need to know n(E)
= n(clubs), which is the number of clubs in a deck of cards and n(S)
= n(cards in a deck), which is the total number of cards in a deck.
What do you think n(E)
= n(clubs) is?
If you said 13 you are correct. There are 13 clubs in a deck of
cards.
What do you think n(S)
= n(cards in a deck) is?
If you said 52 give yourself a pat on the back. There are 52 cards
in a deck.
Putting this together in the Theoretical Probability formula you
get: |
|
*putting in the numbers found above
*reducing the fraction
*rounding to 3 decimal places |
Putting the two probabilities of mutually exclusive events together
we get: |
|
*putting in the numbers found above
*rounding to 3 decimal places |
The probability that a heart or club is dealt
is .5. |
 Answer/Discussion
to 2c Answer/Discussion
to 2c
Find the probability that you are dealt a heart and a club. Round
answer to three decimal places. |
As mentioned in the Answer/Discussion to problem
2b, these two sets are mutually exclusive. This time we are
looking for the probability that is a heart AND a club is dealt.
This means the card must have both attributes. Since they are mutually
exclusive, this means they have nothing in common. In other words,
a card cannot be both a heart and a club at the same time.
So what would the probability of this event be????
If you said 0, you are right on. Since n(a card with a heart and
a club) is 0, the probability will be 0. |
 Answer/Discussion
to 2d Answer/Discussion
to 2d
Find the probability that you are dealt an ace and a spade. Round
answer to three decimal places. |
To find this probability we need to know n(E)
= n(ace AND spade), which is the number of cards with an ace and a spade
on it in a deck of cards and n(S)
= n(cards in a deck), which is the total number of cards in a deck.
What do you think n(E)
= n(ace AND spade) is?
If you said 1 you are correct. There is 1 card in a deck of cards
that has both an ace and a spade on it.
What do you think n(S)
= n(cards in a deck) is?
If you said 52 give yourself a pat on the back. There are 52 cards
in a deck.
Putting this together in the Theoretical Probability formula you
get: |
|
*putting in the numbers found above
*rounding to 3 decimal places |
The probability that a card with an ace and spade on it is dealt
is .019. |
 Answer/Discussion
to 2e Answer/Discussion
to 2e
Find the probability that you are dealt an ace or a spade. Round
answer to three decimal places. |
Note that these two events are NOT mutually exclusive. A card
CAN have an ace or a spade at the same time. So we can use the formula
(property 5): 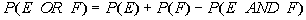
Let's break it down first by finding each separate probability.
P(an ace is dealt)
To find this probability we need to know n(E)
= n(aces), which is the number of aces in a deck of cards and n(S)
= n(cards in a deck), which is the total number of cards in a deck.
What do you think n(E)
= n(aces) is?
If you said 4 you are correct. There are 4 aces in a deck of cards.
What do you think n(S)
= n(cards in a deck) is?
If you said 52 give yourself a pat on the back. There are 52 cards
in a deck.
Putting this together in the Theoretical Probability formula you
get: |
|
*putting in the numbers found above
*reducing the fraction
*rounding to 3 decimal places |
|
P(a spade is dealt)
To find this probability we need to know n(E)
= n(spades), which is the number of spades in a deck of cards and n(S)
= n(cards in a deck), which is the total number of cards in a deck.
What do you think n(E)
= n(spades) is?
If you said 13 you are correct. There are 13 spades in a deck
of cards.
What do you think n(S)
= n(cards in a deck) is?
If you said 52 give yourself a pat on the back. There are 52 cards
in a deck.
Putting this together in the Theoretical Probability formula you
get: |
|
*putting in the numbers found above
*reducing the fraction
*rounding to 3 decimal places |
|
P(an ace AND a spade is dealt)
We found this probability to be 1/52 in the Answer/Discussion
to problem 2d.
Putting the probabilities of non mutually exclusive events together
we get: |
|
*putting in the numbers found above
*rounding to 3 decimal places |
The probability that a card that is dealt has an ace or a spade
on it is .308. |
 Answer/Discussion
to 3a Answer/Discussion
to 3a
Find the probability that 2 freshmen, 2 sophomores and 2 juniors are
selected. Round answer to three decimal places. |
To find this probability we need to know n(E)
= n(2 freshmen, 2 sophomores and 2 juniors are selected), which is the
number of ways 6 names drawn can contain 2 freshmen, 2 sophomores and 2
juniors and n(S) = n(6 name drawings), which
is the total number of ways 6 names can be drawn.
What do you think n(E)
= n(2 freshmen, 2 sophomores and 2 juniors are selected) is?
Since we are counting draws that means we are counting groups of names,
which means we need to use combinations to count them. If you need
a review on combinations, feel free to go to Tutorial
57: Combinations.
If you said 21168 you are correct.
Let's see how we get that number.
Here is what the committee looks like: we would have to have
2 freshmen, 2 sophomores and 2 juniors to meet this condition:
2 FRESHMEN 2 SOPHOMORES
2 JUNIORS
|
|
*Comb. of n = 7 freshmen taken r = 2 at a time
*Comb. of n = 9 sophomores taken r = 2 at
a time
*Comb. of n = 8 juniors taken r = 2 at a time
*Expand 7! until it gets to 5!, 9! until it
gets to 7!, and 8! until it gets to 6! which are the larger !'s in
the den.
*Cancel out 5!'s, 7!'s, and 6!'s
|
As mentioned above, n(E) = n(2 freshmen,
2 sophomores and 2 juniors are selected) = 21168.
If you have a factorial key, you can put it in as 7!, divided by
5!, divided by 2! times 9!, divided by 7!, divided by 2!, times 8!, divided
by 6!, divided by 2! and then press enter or =.
If you don't have a factorial key, you can simplify it as shown above
and then enter it in. |
What do you think n(S)
= n(6 name drawings) is?
If you said 1344904 give yourself a pat on the back.
Again you would have to use combinations to figure this one out.
Overall, there are 7 freshmen, 9 sophomores, 8 juniors, and 10 seniors
for a total of 34 students, taken 6 at a time. |
|
*Comb. of n = 34 students taken r = 6 at a
time
*Eval. inside ( )
*Expand 34! until it gets to 28!
which is the larger ! in the den.
*Cancel out 26!'s
|
As mentioned above, n(S) = n(6 name drawings)
= 1344904.
If you have a factorial key, you can put it in as 34!, divided by
28!, divided by 6! and then press enter or =.
If you don't have a factorial key, you can simplify it as shown above
and then enter it in.
Putting this together in the Theoretical Probability formula you
get: |
|
*putting in the numbers found above
*rounding to 3 decimal places |
The probability that 2 freshmen, 2 sophomores and 2 juniors are
drawn is .016. |
 Answer/Discussion
to 3b Answer/Discussion
to 3b
Find the probability that only seniors are selected. Round answer
to three decimal places. |
To find this probability we need to know n(E)
= n(only seniors are drawn), which is the number of ways 6 names drawn
can contain only seniors and n(S) = n(6 name
drawings), which is the total number of ways 6 names can be drawn.
What do you think n(E)
= n(seniors) is?
Since we are counting draws that means we are counting groups of names,
which means we need to use combinations to count them. If you need
a review on combinations, feel free to go to Tutorial
57: Combinations.
If you said 210 you are correct.
Let's see how we get that number.
Here is what the committee looks like: we would have to have
only seniors to meet this condition:
6 SENIORS
|
|
*Comb. of n = 10 seniors taken r = 6 at a time
*Eval. inside ( )
*Expand 10! until it gets to 6! which is the
larger ! in the den.
*Cancel out 6!'s
|
As mentioned above, n(E) = n(only seniors
are drawn) = 210.
If you have a factorial key, you can put it in as 10!, divided by
4!, divided by 6! and then press enter or =.
If you don't have a factorial key, you can simplify it as shown above
and then enter it in. |
What do you think n(S)
= n(6 name drawings) is?
As shown in Answer/Discussion to problem 3a, n(S)
= n(6 name drawings) = 1344904.
Putting this together in the Theoretical Probability formula you
get: |
|
*putting in the numbers found above
*rounding to 4 decimal places |
The probability that only seniors are drawn is
.0002.
Note I carried this out 4 decimal places since
that was the first non zero digit. |
 Answer/Discussion
to 4a Answer/Discussion
to 4a
Find the probability that a six is rolled the 1st time and an odd number
is rolled a 2nd time. Round answer to three decimal places. |
Since the outcome of the 1st roll of the die does NOT affect the outcome
of the 2nd roll of the die, this means these two
events are independent. So we can use the formula 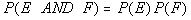 to find our probability.
Let's break it down. |
P(1st roll is a 6)
To find this probability we need to know n(E)
= n(6's on the die), which is the number of 6's on a die and n(S)
= n(numbers on a die), which is the total number of numbers on a die.
What do you think n(E)
= n(6's on the die) is?
If you said 1 you are correct. There is 1 number 6 on a die.
What do you think n(S)
= n(numbers on a die) is?
If you said 6 give yourself a pat on the back. There are 6 numbers on
a die.
Putting this together in the Theoretical Probability formula you
get: |
|
*putting in the numbers found above
*rounding to 3 decimal places
|
|
P(2nd roll is odd)
To find this probability we need to know n(E)
= n(odd numbers on a die), which is the number of odd numbers on a die
and n(S) = n(numbers on a die), which is the
total number of numbers on a die.
What do you think n(E)
= n(odd numbers on a die) is?
If you said 3 you are correct. There is 3 odd numbers on a die.
What do you think n(S)
= n(numbers on a die) is?
If you said 6 give yourself a pat on the back. There are 6 numbers on
a die.
Putting this together in the Theoretical Probability formula you
get: |
|
*putting in the numbers found above
*rounding to 3 decimal places
|
Putting the probabilities of two events that are independent together
we get: |
|
*putting in the numbers found above
*rounding to 3 decimal places
|
 Answer/Discussion
to 4b Answer/Discussion
to 4b
Find the probability that a number less than or equal to 2 is rolled
the 1st time and an even number is rolled the 2nd time. Round answer
to three decimal places. |
Since the outcome of the 1st roll of the die does NOT affect the outcome
of the 2nd roll of the die, this means these two
events are independent. So we can use the formula 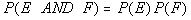 to find our probability.
Let's break it down. |
P(1st roll is less than or equal to 2)
To find this probability we need to know n(E)
= n(numbers less than or equal to 2), which is the number of numbers that
are less than or equal to 2 on a die and n(S)
= n(numbers on a die), which is the total number of numbers on a die.
What do you think n(E)
= n(numbers less than or equal to 2) is?
If you said 2 you are correct. There are 2 numbers that are less than
or equal to 2 on a die.
What do you think n(S)
= n(numbers on a die) is?
If you said 6 give yourself a pat on the back. There are 6 numbers on
a die.
Putting this together in the Theoretical Probability formula you
get: |
|
*putting in the numbers found above
*rounding to 3 decimal places
|
|
P(2nd roll is even)
To find this probability we need to know n(E)
= n(even numbers on a die), which is the number of even numbers on a die
and n(S) = n(numbers on a die), which is the
total number of numbers on a die.
What do you think n(E)
= n(even numbers on a die) is?
If you said 3 you are correct. There is 3 even numbers on a die.
What do you think n(S)
= n(numbers on a die) is?
If you said 6 give yourself a pat on the back. There are 6 numbers on
a die.
Putting this together in the Theoretical Probability formula you
get: |
|
*putting in the numbers found above
*rounding to 3 decimal places
|
Putting the probabilities of two events that are independent together
we get: |
|
*putting in the numbers found above
*rounding to 3 decimal places
|

Last revised on May 16, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.
|
|


