College Algebra
Answer/Discussion to Practice Problems
Tutorial 54D: Geometric Sequences and Series
 Answer/Discussion
to 1a Answer/Discussion
to 1a
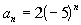
|
Since a geometric sequence is a sequence, you find
the terms exactly the same way that you do a sequence. n is our term number and we
plug the term number into the function to find the value of the term.
If you need a review on sequences, feel free to go to Tutorial 54A: Sequences.
Lets see what we get for
our first five terms:
|
What
would be the common ratio for this problem?
If you said -5 you are correct!
Note that you would have to multiply (-10)(-5) = 50, (50)(-5) = -250,
(-250)(5) = 1250, and (1250)(-5) = -6250. It has to be
consistent throughout the sequence.
Also note that the base that is being raised to a power is -5. |
 Answer/Discussion
to 1b Answer/Discussion
to 1b

|
Since a geometric sequence is a sequence, you find
the terms exactly the same way that you do a sequence. n is our term number and we
plug the term number into the function to find the value of the term.
If you need a review on sequences, feel free to go to Tutorial 54A: Sequences.
Lets see what we get for
our first five terms:
|
What
would be the common ratio for this problem?
If you said 1/4 you are correct!
Note that you would have to multiply by 1/4 each time you go from one
term to the next: (4)(1/4) = 1, (1)(1/4) = 1/4, (1/4)(1/4) =
1/16, and (1/16)(1/4)=1/64. It has to be consistent
throughout the sequence.
Also note that the base that is being raised to a power is 1/4. |
 Answer/Discussion
to 2a Answer/Discussion
to 2a
125, 25, 5, 1, ... |
We will use the nth
term formula for a geometric sequence, 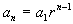 to help us with
this problem.
Basically we need to find two things: the first term of the
sequence, 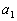 and the
common ratio, r.
What
is 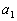 , the first term? , the first term?
If you said 125, give yourself a high five. The first term of
this sequence is 125.
What
is r, the common ratio?
If you said 1/5, you are right!!
Note that you would have to multiply 1/5 each time you go from one term
to the next: (125)(1/5) = 25, (25)(1/5) = 5, and (5)(1/5) =
1. It has to be consistent throughout the sequence.
Putting in 125 for 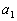 and 1/5 for r we get: and 1/5 for r we get:

|
 Answer/Discussion
to 2b Answer/Discussion
to 2b
4, -12, 36, -108, ...
|
We will use the nth
term formula for a geometric sequence, 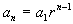 to help us with
this problem.
Basically we need to find two things: the first term of the
sequence, 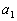 and the
common ratio, r.
What
is 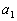 , the first term? , the first term?
If you said 4, give yourself a high five. The first term of this
sequence is 4.
What
is r, the common ratio?
If you said -3, you are right!!
Note that you would have to multiply -3 each time you go from one term
to the next: (4)(-3) = -12, (-12)(-3) = 36, and (36)(-3) =
-108. It has to be consistent throughout the sequence.
Putting in 4 for 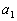 and -3 for r we get: and -3 for r we get:

|
 Answer/Discussion
to 3a Answer/Discussion
to 3a
2 + 14 + 98 + 686 + 4802 + 33614 + 235298
|
We will use the formula for the sum of the first n terms of geometric
sequence, 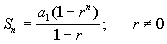 , , to
help us with this problem.
Basically we need to find three things: the first term of the sequence,
the common ratio, and how many terms of the sequence we are adding in
the series.
What
is 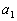 , the first term? , the first term?
If you said 2 you are right!
What
is r, the common
ratio?
If you said 7, give yourself a pat on the back. Note that you would
have to multiply -2 each time you go from one term to the next: (2)(7)
= 14, (14)(7) = 98, (98)(7) = 686, (686)(7) = 4802, (4802)(7) = 33614,
and (33614)(7) = 235298. It has to be consistent throughout
the sequence.
How
many terms are we summing up?
If you said 7, you are correct.
Putting in 2 for the first
term, 7 for the common ratio, and 7 for n, we get:

|
 Answer/Discussion
to 3b Answer/Discussion
to 3b
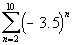
|
We will use the formula for the sum of the first n terms of geometric
sequence, 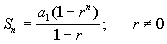 , , to
help us with this problem.
Basically we need to find three things: the first term of the sequence,
the common ratio, and how many terms of the sequence we are adding in
the series.
What
is 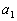 , the first term? , the first term?
If you said 12.25 you are right!
Since this summation starts at 2, you need to plug in 2 into the given
formula:
 What
is r, the common
ratio?
What
is r, the common
ratio?
If you said -3.5, give yourself a pat on the back. Note that -3.5
is the number that is being raised to the exponent. So each time
the number goes up on the exponent, in essence you are multiplying it
by -3.5.
How
many terms are we summing up?
If you said 9, you are correct. If you start at 2 and go all the
way to 10, there will be 9 terms.
Putting in 12.25 for the
first
term, -3.5 for the common ratio, and 9 for n, we get:

|
 Answer/Discussion
to 4a Answer/Discussion
to 4a
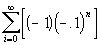
|
We will use the formula for the sum of infinite
geometric sequence,  , , to help us with this problem.
Basically we need to find two things: the first term of the sequence
and the common ratio.
What
is the first term, 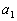 ? ?
If you said -1 you are right!
Since this summation starts at 0, you need to plug in 0 into the given
formula:
 What
is the common ratio, r?
What
is the common ratio, r?
If you said -.1, give yourself a pat on the back. Note that -.1 is the
number that is being raised to the exponent. So each time the
number goes up on the exponent, in essence you are multiplying it by
-.1.
Putting in -1 for the
first term and -.1 for the common ratio we get:

|
 Answer/Discussion
to 4b Answer/Discussion
to 4b
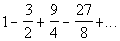
|
We will use the formula for the sum of infinite
geometric sequence,  , , to help us with this problem.
Basically we need to find two things: the first term of the sequence
and the common ratio.
What
is the first term, 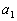 ? ?
If you said 1 you are right!
What
is the common ratio, r?
If you said -3/2, give yourself a pat on the back. Note that you would
have to multiply -3/2 each time you go from one term to the next:
(1)(-3/2)
= -3/2, (-3/2)(-3/2) = 9/4, (9/4)(-3/2) = -27/8. It has to
be consistent
throughout the sequence.
Since the geometric ratio
is -3/2 and  ,
there
is no sum. ,
there
is no sum.
|

Last revised on May 16, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.
|
|


