College Algebra
Answer/Discussion to Practice Problems
Tutorial 54A: Sequences
 Answer/Discussion
to 1a
 ; 1 < n < 5
|
Basically, to find the nth term of a sequence works
in the same fashion as function notation. If you want to find the
3rd term, you are looking for 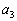 , which means you
plug in 3 for n into the given function.
So, what are we going to plug in for n to find the 1st term?
If you said 1, give yourself a pat on the back. What about the
2nd term? I hope you said you would plug in 2 for n.
Since we have to go from 1 < n < 5, this means we need
to find 5 terms and we will be plugging in 1, 2, 3, 4, and 5 for n.
Let's see what we get:
|
Note how we had -1 raised to n, which changes value, and
the signs of the terms alternated.
The five terms of this
sequence are 1/4, -1/8, 1/16, -1/32, and 1/64.
|
Answer/Discussion
to 2a
|
This function contains a factorial.
Let's see what we get for our first five terms:
|
Now let's check out
the twelfth term:
|
Answer/Discussion
to 3a
|
Let's take a look at
what is happening here:
Something that is always
constant is that each term contains e.
There are also two things that
change.
First
let's look at the alternating signs:
For it to have
alternating signs, we need to have (-1) raised to a power that
changes. This means n,
the term number is involved.
The first term is positive, the second term is negative, the third
positive, the fourth negative and so forth.
When n is odd (1,
3, 5, ...), then the term is positive.
When n is even (2,
4, 6, ...), then the term is negative.
So do you think we are going to have 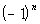 or  .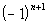
If you said 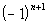you are
correct!!! If n is odd, then this term will be positive. If n is even, then this term
will be negative.
|
We also have the exponent
on each term.
Again
we need to figure out the relationship between n and the exponent:
When n is 1, the exponent is 1.
When n is 2, the
exponent is 4.
When n is 3, the exponent is
9.
When n is 4, the
exponent is 16.
|
What
do you think the relationship is?
It looks like the exponent is always n squared.
Putting it together, the
formula for the nth term is  .
Sometimes you have to play around with it before you get it just
right. You can always check it by putting in the n values and seeing if you
get the given sequence.
This one does check.
|
We are giving the first term,  . Using that
we can find the
second term and so forth.
Let's see what we get for
our first three terms:
|
Since this is a
recursive formula, in order to the fifth term, we need to find the
fourth term:
|
Last revised on May 16, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.
|
|
; 
