College Algebra
Answer/Discussion to Practice Problems
Tutorial 49: Solving Systems of
Linear Equations in Two Variables

WTAMU > Virtual Math Lab > College Algebra > Tutorial 49: Solving Systems of Linear Equations in Two Variables

Answer/Discussion to 1a

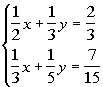
problem 1a

I’m going to chose to use the elimination by addition method, however it would be perfectly find for you to use the substitution method. Either way the answer will be the same.

Step 1: Simplify and put both equations in the form Ax + By = C if needed.

This equation is full of those nasty fractions. We can simplify both equations by multiplying each separate one by it’s LCD, just like you can do when you are working with one equation. As long as you do the same thing to both sides of an equation, you keep the two sides equal to each other.

Multiplying each equation by it's respective LCD we get:

*Mult. by LCD of 6

*Mult. by LCD of 15

Step 2: Multiply one or both equations by a number that will create opposite coefficients for either x or y if needed.

Again, you want to make this as simple as possible.

Note how the coefficient on y in the first equation is 2 and in the second equation it is 3. We need to have opposites, so if one of them is 6 and the other is -6, they would cancel each other out when we go to add them. If we added them together the way they are now, we would end up with one equation and two variables, nothing would drop out. And we would not be able to solve it.

So I proposed that we multiply the first equation by 3 and the second equation by -2, this would create a 10 and a -10 in front of the y’s and we will have our opposites.

Multiplying the first equation by 3 and the second equation by -2 we get:

*Mult. both sides of 1st eq. by 3
*Mult. both sides of 2nd eq. by -2

*y's have opposite coefficients

Step 3: Add equations.

*Note that y's dropped out

Step 4: Solve for remaining variable.

Step 5: Solve for second variable.

You can choose any equation used in this problem to plug in the found x value.

I choose to plug in 2 for x into the first simplified equation (found in step 1) to find y’s value.

*Plug in 2 for x

*Inverse of add 6 is sub. 6

*Inverse of mult. by 2 is div. by 2

Step 6: Check the proposed ordered pair solution in BOTH original equations.

You will find that if you plug the ordered pair (2, -1) into BOTH equations of the original system, that this is a solution to BOTH of them.

(2, -1) is a solution to our system.

(return to problem 1a)

Answer/Discussion to 1b

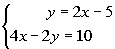
problem 1b

I’m going to chose to use the substitution method, however it would be perfectly find for you to use the elimination by addition method. Either way the answer will be the same.

Step 1: Simplify if needed.

Both of these equations are already simplified. No work needs to be done here.

Step 2: Solve one equation for either variable.

Note how the first equation is already solved for y. We can use that one for this step.

It does not matter which equation or which variable you choose to solve for. But it is to your advantage to keep it as simple as possible.

First equation solved for y:

*Solved for y

Step 3: Substitute what you get for step 2 into the other equation
AND
Step 4: Solve for the remaining variable.

Substitute the expression 2x - 5 for y into the second equation and solve for x:
(when you plug in an expression like this, it is just like you plug in a number for your variable)

*Sub. 2x - 5 for y

*Variable dropped out AND true

Wait a minute, where did our variable go????

As mentioned above, if the variable drops out AND we have a TRUE statement, then when have an infinite number of solutions. They end up being the same line.

Step 5: Solve for second variable.

Since we did not get a value for x, there is nothing to plug in here.

Step 6: Check the proposed ordered pair solution in BOTH original equations.

There is no value to plug in here.

When they end up being the same equation, you have an infinite number of solutions. You can write up your answer by writing out either equation to indicate that they are the same equation.

Two ways to write the answer are {(x, y)| y = 2x - 5} OR {(x, y) | 4x - 2y = 10}.

(return to problem 1b)

Answer/Discussion to 1c

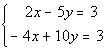
problem 1c

I’m going to chose to use the elimination by addition method, however it would be perfectly find for you to use the substitution method. Either way the answer will be the same.

Step 1: Simplify and put both equations in the form Ax + By = C if needed.

Both of these equations are already simplified and in the right form. No work needs to be done here.

Step 2: Multiply one or both equations by a number that will create opposite coefficients for either x or y if needed.

Again, you want to make this as simple as possible.

Note how the coefficient on x in the first equation is 2 and in the second equation it is -4. We need to have opposites, so if one of them is 4 and the other is -4, they would cancel each other out when we go to add them. If we added them together the way they are now, we would end up with one equation and two variables, nothing would drop out. And we would not be able to solve it.

So I proposed that we multiply the first equation by 2, this would create a 4 and a -4 in front of the x’s and we will have our opposites.

Multiplying the first equation by 2 we get:

*Mult. both sides of 1st eq. by 2

*x's and y's have opposite coefficients

Step 3: Add equations.

*Note that x's and y's both dropped out

Step 4: Solve for remaining variable.

Wait a minute, where did our variable go????

As mentioned above if your variable drops out and you have a FALSE statement, then there is no solution. If we were to graph these two, they would be parallel to each other.

Step 5: Solve for second variable.

There is no value to plug in here.

Step 6: Check the proposed ordered pair solution in BOTH original equations.

There is no value to plug in here.

The answer is no solution.

(return to problem 1c)

Answer/Discussion to 2a

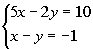
problem 1a