Title
West Texas A&M University - Home
Virtual Math Lab

College Algebra
Answer/Discussion to Practice Problems  
Tutorial 43: Logarithmic Functions


 

checkAnswer/Discussion to 1a

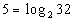
problem 1a

 
We want to use the definition: 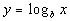log definition     if and only if 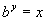log definition.

First, let's figure out what the base needs to be.  What do you think?  It looks like the b in the definition correlates with 2 in our problem - so our base is going to be 2. 

Next, let's figure out the exponent.  This is very key, again remember that logs are another way to write exponents.  This means the log is set equal to the exponent, so in this problem that means that the exponent has to be 5.

That leaves 32 to be what the exponential expression is set equal to.

Putting all of this into the log definition we get:

 
ad1a
*Rewriting in exponential form

 
Hopefully, when you see it written in exponential form you can tell that it is a true statement.  In other words, when we take 2 to the 5th power we do get 32.  

 

 


 

checkAnswer/Discussion to 1b

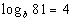
problem 1b

 
We want to use the definition: 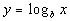log definition     if and only if 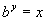log definition.

First, let's figure out what the base needs to be.  What do you think?  It looks like the b in the definition correlates with b in our problem - so our base is going to be b. 

Next, let's figure out the exponent.  This is very key, again remember that logs are another way to write exponents.  This means the log is set equal to the exponent, so in this problem that means that the exponent has to be 4.

That leaves 81 to be what the exponential expression is set equal to.

Putting all of this into the log definition we get:

 
ad1b
*Rewriting in exponential form

 

 


 

checkAnswer/Discussion to 2a

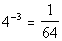
problem 2a

 
We want to use the definition: 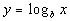log definition     if and only if 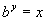log definition.

First, let's figure out what the base needs to be.  What do you think?  It looks like the b in the definition correlates with 4 in our problem - so our base is going to be 4. 

Next, let's figure out the exponent.  In this direction it is easy to note what the exponent is because we are more used to it written in this form, but when we write it in the log form we have to be careful to place it correctly.  Looks like the exponent is -3, don't you agree? 

The value that the exponential expression is set equal to is what goes inside the log function.  In this problem that is 1/64. 

Let's see what we get when we put this in log form:

 
ad2a
*Rewriting in log form

 

 


 

checkAnswer/Discussion to 2b

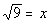
problem 2b

 
We want to use the definition: 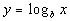log definition     if and only if 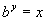log definition.

Rewriting the original problem using exponents we get:

ad2b1

First, let's figure out what the base needs to be.  What do you think?  It looks like the b in the definition correlates with 9 in our problem - so our base is going to be 9. 

Next, let's figure out the exponent.  In this direction it is easy to note what the exponent is because we are more used to it written in this form, but when we write it in the log form we have to be careful to place it correctly.  Looks like the exponent is 1/2, don't you agree? 

The value that the exponential expression is set equal to is what goes inside the log function.  In this problem that is x. 

Let's see what we get when we put this in log form:

 
ad2b2
*Rewriting in log form

 

 


 

checkAnswer/Discussion to 3a

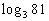
problem 3a

 
When we are looking for the log itself, keep in mind that logs are another way to write exponents. 
The thought behind this is, we are wanting the power that we would need to raise 3 to to get 81. 

 
Step 1: Set the log equal to x
AND
Step 2:  Use the definition of logs shown above to write the equation in exponential form
AND
Step 3: Find x.

 
ad3a

*Setting the log = to x
 

*Rewriting in exponential form

*x is the exponent we need on 3 to get 81

 
So the exponent we were looking for is 4.

 

 


 

checkAnswer/Discussion to 3b

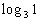
problem 3b

 
When we are looking for the log itself, keep in mind that logs are another way to write exponents. 
The thought behind this is, we are wanting the power that we would need to raise 3 to to get 1. 

 
Step 1: Set the log equal to x
AND
Step 2:  Use the definition of logs shown above to write the equation in exponential form
AND
Step 3: Find x.

 
ad3b

*Setting the log = to x
 

*Rewriting in exponential form

*x is the exponent we need on 3 to get 1

 
So the exponent we were looking for is 0.

 

 


 

checkAnswer/Discussion to 3c

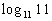
problem 3c

 
When we are looking for the log itself, keep in mind that logs are another way to write exponents. 
The thought behind this is, we are wanting the power that we would need to raise 11 to to get 11. 

 
Step 1: Set the log equal to x
AND
Step 2:  Use the definition of logs shown above to write the equation in exponential form
AND
Step 3: Find x.

 
ad3c

*Setting the log = to x
 

*Rewriting in exponential form

*x is the exponent we need on 11 to get 11

 
So the exponent we were looking for is 1.

 

 


 

checkAnswer/Discussion to 3d

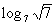
problem 3d

 
When we are looking for the log itself, keep in mind that logs are another way to write exponents. 
The thought behind this is, we are wanting the power that we would need to raise 7 to get square root of 7. 

 
Step 1: Set the log equal to x
AND
Step 2:  Use the definition of logs shown above to write the equation in exponential form
AND
Step 3: Find x.

 
ad3d

*Setting the log = to x
 

*Rewriting in exponential form

*x is the exponent we need on 7 to get square root of 7

 
So the exponent we were looking for is 1/2.

 

 


 

checkAnswer/Discussion to 4a

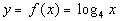
problem 4a

 
Step 1:  Use the definition of logs shown above to write the equation in exponential form. 

 
First, we need to write in exponential form, just like we practiced in examples 1 and 2 on the lesson page.

Looks like the base is 4, the exponent is y, and the log will be set = to x:

 
ad4a1

*Rewriting in exponential form

 
Step 2:  Plug in values for y (NOT x) to find some ordered pairs.

 
I have found that the best way to do this is to do it the same each time.  In other words, put in the same values for y each time and then find it's corresponding x value for the given function.

The first two columns just show what values we are going to plug in for y.

The last three columns show the corresponding values for x and y for the given function.
 

x
y
 
ad4a2b
y
(x, y)
 
-2 
 
ad4a2
-2
(1/16, -2)
 
-1
 
ad4a3
-1 
(1/4, -1)
 
 0
 
ad4a4
0
(1, 0)
 
 1
 
ad4a5
1
(4, 1)
 
 2
 
ad4a6
2
(16, 2)

 
Step 3: Plot points.
AND
Step 4: Draw a curve.

 
ad4a7

 

 


 

checkAnswer/Discussion to 4b

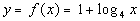
problem 4b

 
Step 1:  Use the definition of logs shown above to write the equation in exponential form. 

 
Setting this up to be able to use the definition we get:

ad4b1
 

Next, we need to write in exponential form, just like we practiced in examples 1 and 2 on the lesson page.

Looks like the base is 4, the exponent is y - 1, and the log will be set = to x:

 
ad4b2

*Rewriting in exponential form

 
Step 2:  Plug in values for y (NOT x) to find some ordered pairs.

 
I have found that the best way to do this is to do it the same each time.  In other words, put in the same values for y each time and then find it's corresponding x value for the given function.

The first two columns just show what values we are going to plug in for y.

The last three columns show the corresponding values for x and y for the given function.
 

x
y
 
ad42b2
y
(x, y)
 
-2 
 
ad4b3
-2
(1/64, -2)
 
-1
 
ad4b4
-1 
(1/16, -1)
 
 0
 
ad4b5
0
(1/4, 0)
 
 1
 
ad4b6
1
(1, 1)
 
 2
 
ad4b7
2
(4, 2)

 
Step 3: Plot points.
AND
Step 4: Draw a curve.

 
ad4b8

 

 


 

checkAnswer/Discussion to 5a

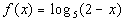
problem 5a

 
Based on the definition of logs, the inside of the log has to be positive. 

Since x is part of the inside of the log on this problem we need to find a value of x, such that the inside of the log, 2 - x, is positive.

 
ad5a
*Inside of log must be positive
*Solve the inequality
 
 
 

*Domain of this function

 
The domain is x < 2. 

That means that if we put in any value of x that is less than 2, we will end up with a positive value inside our log.

 

 


 

checkAnswer/Discussion to 6a

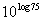
problem 6a

 
I'm going to use the second inverse property shown on the lesson page:

 
ad6a
*log has a base of 10

 

 


 

checkAnswer/Discussion to 6b

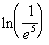
problem 6b

 
We can either use the definition of logs, as shown above, or the inverse properties of logs to evaluate this.

I'm going to use the first inverse property shown on the lesson page:

 
ad6b
*Rewrite 1/e^5 as e to the -5th power
 
 

 

 

 


 

checkAnswer/Discussion to 7a

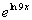
problem 7a

 
I'm going to use the second inverse property shown on the lesson page:

 
ad7a
*ln has a base of e
 
 

 

 

 


 

checkAnswer/Discussion to 7b

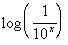
problem 7b

 
I'm going to use the first inverse property shown on the lesson page:

 
ad7b
*log has a base of 10
 
 

 

 

 

Buffalo top

 


Last revised on March 17, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.