Title
West Texas A&M University - Home
Virtual Math Lab

College Algebra
Answer/Discussion to Practice Problems  
Tutorial 42: Exponential Functions


 

checkAnswer/Discussion to 1a

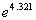
problem 1a

 
ad1a

 
Try this using your calculator and see if you get the answer that I got.  If you didn't, refer back to e key on calculator that I have above.

 

 


 

checkAnswer/Discussion to 1b

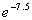
problem 1b

 
ad1b

 
Try this using your calculator and see if you get the answer that I got.  If you didn't, refer back to e key on calculator that I have above.

 

 


 

checkAnswer/Discussion to 2a

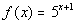
problem 2a

 
Note that the base = 5 and the exponent is our variable x + 1.  There is one outside factor, we are adding 1 to our variable x in the exponent

 

 
I have found that the best way to do this is to do it the same each time.  In other words, put in the same values for x each time and then find it's corresponding y value for the given function.
 
 
x
ad2a1
(x, y)
-2
ad2a2
(-2, .2)
-1
ad2a3
(-1, 1)
0
ad2a4
(0, 5)
1
ad2a5
(1, 25)
2
ad2a6
(2, 125)

 
Step 2: Plot points.
AND
Step 3: Draw curve.

 
ad2a7

 

 


 

checkAnswer/Discussion to 2b

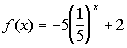
problem 2b
Note that the base = 1/5 and the exponent is our variable x.  There are 2 outside factors, we are multiplying it by -5  AND we are adding 2 to our base after we raise it to the exponent x and multiply that by -5. 

 

 
I have found that the best way to do this is to do it the same each time.  In other words, put in the same values for x each time and then find it's corresponding y value for the given function.
 
 
x
ad2b1
(x, y)
-2
ad2b2
(-2, -123)
-1
ad2b3
(-1, -23)
0
ad2b4
(0, -3)
1
ad2b5
(1, 1)
2
ad2b6
(2, 1.8)

 
Step 2: Plot points.
AND
Step 3: Draw curve.

 
ad2b7

 

 


 

checkAnswer/Discussion to 3a

$7500 for 25 years at an annual rate of 4.25% compounded monthly. 

 
P = 7500
r = 4.25% = .0425
t = 25
n = monthly = 12 times a year

 
ad3a
 

*Plug in values shown above into compound form.

*Find number inside the (  ) first

*Raise the (  )  to the 300th power
*Multiply

 
So the compound AMOUNT would be $21661.27

The compound amount is the total amount that is in the account. How do you think we are going to get the interest?? Well we have the principle which is the beginning amount and we have the compound amount which is the end result. Looks like, if we take the difference of the two, that will give us how much interest was earned from beginning to end. What do you think? 

Compound amount - principle: 21661.27 - 7500 = 14161.27

So our compound interest is $14161.27

 

 


 

checkAnswer/Discussion to 3b

$3000 for 20 years at an annual rate of 6% compounded quarterly. 
P = 3000
r = 6% = .06
t = 20
n = quarterly = 4 times a year

 
ad3b
 

*Plug in values shown above into compound form.

*Find number inside the (  ) first

*Raise the (  )  to the 300th power
*Multiply

 
So the compound AMOUNT would be $9871.99

The compound amount is the total amount that is in the account. How do you think we are going to get the interest?? Well we have the principle which is the beginning amount and we have the compound amount which is the end result. Looks like, if we take the difference of the two, that will give us how much interest was earned from beginning to end. What do you think? 

Compound amount - principle: 9871.99 - 3000 = 6871.99 

So our compound interest is $6871.99

 

 


 

checkAnswer/Discussion to 4a

$8000 that is compounded continuously for 10 years at an interest rate of 5.5%.

 
P =  8000
r = 5.5% = .055
t = 10

 
ad4a2

*Plug in values shown above into compound form.

*Raise e to the .55th power

*Multiply
 

 
So the accumulated or compound AMOUNT would be $13866.02.

 

 

Buffalo top

 


Last revised on March 17, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.