College Algebra
Tutorial 38: Zeros of Polynomial Functions, Part I:
Rational Zero Theorem and Descartes' Rule of Signs
 Learning Objectives Learning Objectives
After completing this tutorial, you should be able to:
- List all possible rational zeros using the Rational Zero Theorem.
- Find all zeros of a polynomial function.
- Use Descartes' Rule of Signs to determine the possible number of
positive
and negative real zeros of a polynomial function.
|
 Introduction Introduction
In this tutorial we will be taking a close look at
finding zeros of
polynomial functions. We will be using things like the Rational
Zero
Theorem and Descartes's Rule of Signs to help us through these
problems.
Basically when you are finding a zero of a function, you are looking
for
input values that cause your functional value to be equal to
zero.
Sounds simple enough. However, sometimes the polynomial has a
degree
of 3 or higher, which makes it hard or impossible to factor. Some
of the ideas covered in this tutorial can help you to break down higher
degree polynomial functions into workable factors. We will be
using
synthetic division to help us out with this process. If you need
a review on synthetic division, feel free to go to Tutorial
37: Synthetic Division and the Remainder and Factor Theorems. |
 Tutorial Tutorial
We can use this theorem to help us find all of the
POSSIBLE rational
zeros or roots of a polynomial function. |
Step 1: List all of the
factors of the constant. |
In the Rational Zero Theorem, p represents
factors of the constant term.
Make sure that you include both the positive and
negative factors. |
Step 2: List all of the
factors of the leading coefficient. |
In the Rational Zero Theorem, q represents
factors of the leading coefficient.
Make sure that you include both the positive and
negative factors. |
Step 3: List all the
POSSIBLE rational zeros or roots. |
This list comes from taking all the factors of the
constant ( p)
and writing them over all the factors of the leading coefficient ( q),
to get a list of 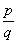 .
Make sure that you get ever possible combination of these factors,
written
as 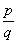 . |
 Example
1 Example
1: Use the Rational Zero Theorem to list all the
possible
rational zeros for 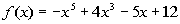 . |
The factors of the constant term 12 are 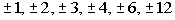 . |
The factors of the leading coefficient -1 are 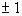 . |
Writing the possible factors as 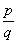 we get:
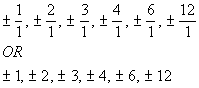
Generally we don’t write a number over 1, I just did it
to emphasize
that the denominator comes for factors of q which are 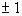 .
It would have been ok to write out the 2nd line without writing out the
1st line. .
It would have been ok to write out the 2nd line without writing out the
1st line. |
 Example
2 Example
2: Use the Rational Zero Theorem to list all the
possible
rational zeros for 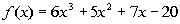 . |
The factors of the constant term -20 are 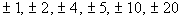 . |
The factors of the leading coefficient 6 are 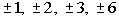 . . |
Writing the possible factors as 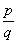 we get:
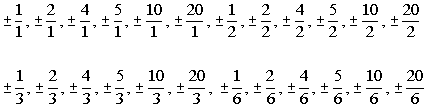
Note, how when you reduce down the fractions, some of
them are repeated.
Here is a final list of all the POSSIBLE rational
zeros, each one
written once and reduced:
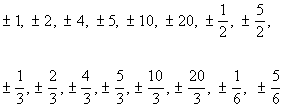
|
 Example
3 Example
3: List all of the possible zeros, use synthetic
division
to test the possible zeros, find an actual zero, and use the actual
zero
to find all the zeros of 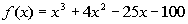 . |
List all of
the possible zeros:
The factors of the constant term 100 are 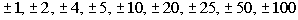 . .
The factors of the leading coefficient 1 are 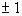 . .
Writing the possible factors as 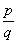 we get: we get:
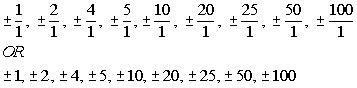
|
Use synthetic
division to test
the possible zeros and find an actual zero:
Recall that if you apply synthetic division and the
remainder is 0,
then c is a zero or root of the
polynomial
function.
If you need a review on synthetic division, feel free to
go to Tutorial
37: Synthetic Division and the Remainder and Factor Theorems.
At this point you are wanting to pick any POSSIBLE
rational root form
the list of 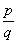 .
I would suggest to start with smaller easier numbers and then go from
there. .
I would suggest to start with smaller easier numbers and then go from
there.
I’m going to choose 2 to try:
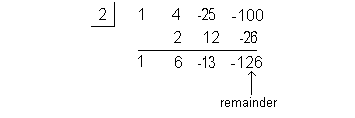
Since the reminder came out -126, this means f(2)
= -126, which means x = 2 is NOT a zero
for
this polynomial function.
That doesn’t mean that we pack up our bags and
quit. It’s back
to the drawing board.
We need to choose another number that comes from that
same list of POSSIBLE
rational roots.
This time I’m going to choose -2:
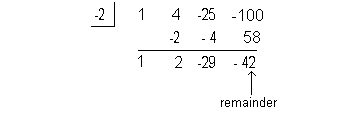
Again, the reminder is not 0, so x = -2
is not a zero of this polynomial function.
This time let’s choose - 4:
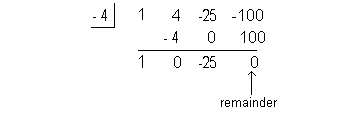
At last, we found a number that has a remainder of 0.
This means that x = - 4 is a zero or root of our polynomial function. |
Use the actual
zero to find
all the zeros:
Since, x = - 4 is a zero,
that means x + 4 is a factor of our polynomial function.
Rewriting f(x)
as (x + 4)(quotient) we get:
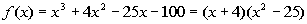
We need to finish this problem by setting this equal
to zero and
solving it: |
|
*Set 1st factor = 0
*Set 2nd factor = 0
*Set 3rd factor = 0
|
The zeros of this function are x = -
4, -5, and 5. |
 Example
4 Example
4: List all of the possible zeros, use synthetic division to
test the possible zeros, find an actual zero, and use the actual zero
to
find all the zeros of 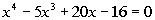 . |
List all of
the possible zeros:
The factors of the constant term -16 are 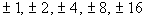 . .
The factors of the leading coefficient 1 are 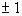 . .
Writing the possible factors as 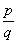 we get: we get:
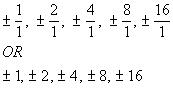
|
Use synthetic
division to test
the possible zeros and find an actual zero:
Recall that if you apply synthetic division and the
remainder is 0,
then c is a zero or root of the
polynomial
function.
If you need a review on synthetic division, feel free to
go to Tutorial
37: Synthetic Division and the Remainder and Factor Theorems.
At this point you are wanting to pick any POSSIBLE
rational root form
the list of 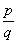 .
I would suggest to start with smaller easier numbers and then go from
there. .
I would suggest to start with smaller easier numbers and then go from
there.
I’m going to choose -1 to try:
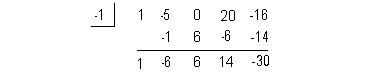
Since the reminder came out -30, this means f(-1)
= -30, which means x = -1 is NOT a zero
for
this polynomial function.
That doesn’t mean that we pack up our bags and
quit. It’s back
to the drawing board.
We need to choose another number that comes from that
same list of POSSIBLE
rational roots.
This time I’m going to choose 1:
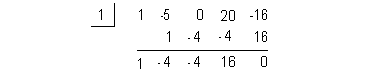
At last, we found a number that has a remainder of 0.
This means that x = 1 is a zero or root of our polynomial function. |
Use the actual
zero to find
all the zeros:
Since, x = 1 is a zero,
that means x - 1 is a factor of our polynomial function.
Rewriting f(x)
as (x - 1)(quotient) we get:
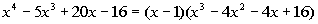
We need to finish this problem by setting this equal
to zero and
solving it: |
|
*Factor the difference
of squares
*Set 1st factor = 0
*Set 2nd factor = 0
*Set 3rd factor = 0
*Set 4th factor = 0
|
The zeros of this function are x = 1,
4, -2 and 2. |
Let 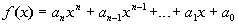 be a polynomial where 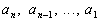 are real coefficients.
The number of POSITIVE REAL
ZEROS of f is either equal to the number of sign changes of successive terms of f(x)
or is less than that number by an even number (until 1 or 0 is
reached).
The number of NEGATIVE REAL
ZEROS of f is either equal to the number of sign changes of successive terms of f(-x)
or is less than that number by an even integer (until 1 or 0 is
reached).
This can help narrow down your possibilities when you do
go on to find
the zeros. |
 Example
5 Example
5: Find the possible number of positive and negative
real
zeros of 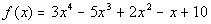 using
Descartes’ Rule of Signs. |
In this problem it isn’t asking for the zeros
themselves, but what
are the possible number of them. This can help narrow down your
possibilities
when you do go on to find the zeros.
Possible number
of positive real
zeros:
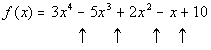
The up arrows are showing where there are sign changes
between successive
terms, going left to right. The first arrow on the left shows a
sign
change from positive 3 to negative 5. The 2nd arrow shows a sign
change from negative 5 to positive 2. The third arrow shows a
sign
change from positive 2 to negative 1. And the last arrow shows a
sign change from negative 1 to positive 10.
There are 4 sign changes between successive terms, which
means that
is the highest possible number of positive real zeros. To find
the
other possible number of positive real zeros from these sign changes,
you
start with the number of changes, which in this case is 4, and then go
down by even integers from that number until you get to 1 or 0.
Since we have 4 sign changes with f(x),
then there is a possibility of 4 or 4 - 2 = 2 or 4 - 4 = 0
positive
real zeros. |
Possible
number of negative
real zeros:
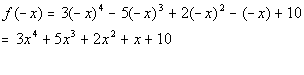
Note how there are no sign changes between successive terms.
This means there are no negative real zeros.
Since we are counting the number of possible real zeros,
0 is the lowest
number that we can have. This piece of information would be
helpful
when determining real zeros for this polynomial. However, for
this
problem we will stop here. |
 Example
6 Example
6: Find the possible number of positive and negative
real
zeros of 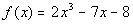 using
Descartes’ Rule of Signs. |
In this problem it isn’t asking for the zeros
themselves, but what
are the possible number of them. This can help narrow down your
possibilities
when you do go on to find the zeros.
Possible number
of positive real
zeros:
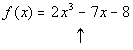
The up arrow is showing where there is a sign change
between successive
terms, going left to right. This arrow shows a sign change from
positive
2 to negative 7.
There is only 1 sign change between successive terms,
which means that
is the highest possible number of positive real zeros. To find
the
other possible number of positive real zeros from these sign changes,
you
start with the number of changes, which in this case is 1, and then go
down by even integers from that number until you get to 1 or 0.
If we went down by even integers from 1, we would be in
the negative
numbers, which is not a feasible answer, since we are looking for the
possible
number of positive real zeros. In other words, we can’t have a -1
of them.
Therefore, there is exactly 1 positive real zero. |
Possible
number of negative
real zeros:
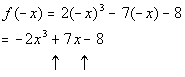
The up arrows are showing where there are sign changes
between successive
terms, going left to right. The first arrow on the left shows a
sign
change from negative 2 to positive 7. The 2nd arrow shows a sign
change from positive 7 to negative 8.
There are 2 sign changes between successive terms, which
means that
is the highest possible number of negative real zeros. To find
the
other possible number of negative real zeros from these sign changes,
you
start with the number of changes, which in this case is 2, and then go
down by even integers from that number until you get to 1 or 0.
Since we have 2 sign changes with f(-x),
then there is a possibility of 2 or 2 - 2 = 0 negative real zeros. |
 Example
7 Example
7: List all of the possible zeros, use Descartes’
Rule
of Signs to possibly narrow it down, use synthetic division to test the
possible zeros and find an actual zero, and use the actual zero to find
all the zeros of 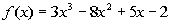 . |
List all of
the possible zeros:
The factors of the constant term -2 are 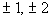 . .
The factors of the leading coefficient 3 are 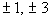 . .
Writing the possible factors as 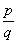 we get: we get:
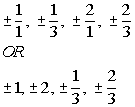
|
Before we try any of these, let’s apply Descartes’
Rule of Signs to
see if it can help narrow down our search for a rational zero.
Possible number
of positive real
zeros:
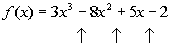
The up arrows are showing where there are sign changes
between successive
terms, going left to right.
There are 3 sign changes between successive terms, which
means that
is the highest possible number of positive real zeros. To find
the
other possible number of positive real zeros from these sign changes,
you
start with the number of changes, which in this case is 3, and then go
down by even integers from that number until you get to 1 or 0.
Since we have 3 sign changes with f(x),
then there is a possibility of 3 or 3 - 2 = 1 positive real zeros. |
Possible
number of negative
real zeros:
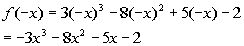
Note how there are no sign changes between successive
terms.
This means there are no negative real zeros.
Since we are counting the number of possible real zeros,
0 is the lowest
number that we can have. This will help us narrow things down in the
next
step. |
Use synthetic
division to test
the possible zeros and find an actual zero:
Recall that if you apply synthetic division and the
remainder is 0,
then c is a zero or root of the
polynomial
function.
If you need a review on synthetic division, feel free to
go to Tutorial
37: Synthetic Division and the Remainder and Factor Theorems.
At this point you are wanting to pick any POSSIBLE
rational root form
the list of 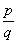 .
Above, we found that there are NO negative
rational
zeros, so we do not have to bother with trying any negative
numbers. See how Descartes’ has helped us. I would suggest
to start with smaller easier numbers and then go from there. .
Above, we found that there are NO negative
rational
zeros, so we do not have to bother with trying any negative
numbers. See how Descartes’ has helped us. I would suggest
to start with smaller easier numbers and then go from there.
I’m going to choose 1 to try:
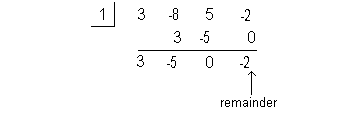
Since the reminder came out -2, this means f(1)
= -2, which means x = 1 is NOT a zero
for this
polynomial function.
That doesn’t mean that we pack up our bags and
quit. It’s back
to the drawing board.
We need to choose another number that comes from that
same list of POSSIBLE
rational roots.
This time I’m going to choose 2:
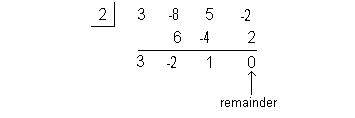
At last, we found a number that has a remainder of 0.
This means that x = 2 is a zero or root of our polynomial function. |
Use the actual
zero to find
all the zeros:
Since, x = 2 is a zero,
that means x - 2 is a factor of our polynomial function.
Rewriting f(x)
as (x - 2)(quotient) we get:
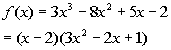
We need to finish this problem by setting this equal
to zero and
solving it: |
|
*Set 1st factor = 0
*Set 2nd factor = 0
*This is a quadratic that does not
factor
*Use the quadratic
formula
|
The zeros of this function are x = 2, 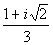 ,
and ,
and 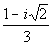 . . |
 Example
8 Example
8: List all of the possible zeros, use Descartes’
Rule
of Signs to possibly narrow it down, use synthetic division to test the
possible zeros and find an actual zero, and use the actual zero to find
all the zeros of 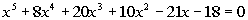 . |
List all of
the possible zeros:
The factors of the constant term -18 are 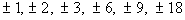 . .
The factors of the leading coefficient 1 are 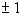 . .
Writing the possible factors as 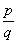 we get: we get:
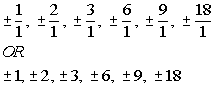
|
Before we try any of these, let’s apply Descartes’
Rule of Signs to
see if it can help narrow down our search for a rational zero.
Possible number
of positive real
zeros:
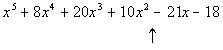
The up arrow is showing where there is a sign change
between successive
terms, going left to right.
There is 1 sign change between successive terms, which
means that is
the highest possible number of positive real zeros.
Since we have 1 sign change with f(x),
then there is exactly 1 positive real zero. |
Possible
number of negative
real zeros:
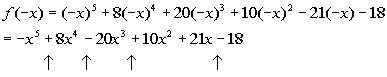
The up arrows are showing where there are sign changes
between successive
terms, going left to right.
There are 4 sign changes between successive terms, which
means that
is the highest possible number of negative real zeros. To find
the
other possible number of negative real zeros from these sign changes,
you
start with the number of changes, which in this case is 4, and then go
down by even integers from that number until you get to 1 or 0.
Since we have 4 sign changes with f(x),
then there are possibility of 4, 4 - 2 = 2 or 4 - 4 = 0 negative real
zeros. |
Use synthetic
division to test
the possible zeros and find an actual zero:
Recall that if you apply synthetic division and the
remainder is 0,
then c is a zero or root of the
polynomial
function.
If you need a review on synthetic division, feel free to
go to Tutorial
37: Synthetic Division and the Remainder and Factor Theorems.
At this point you are wanting to pick any POSSIBLE
rational root from
the list of 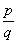 .
Above, we found that there is exactly 1 positive rational zero.
Since
we know that there is 1 for sure, then we may want to go ahead and start
with trying positive rational roots. I would
suggest
to start with smaller easier numbers and then go from there. .
Above, we found that there is exactly 1 positive rational zero.
Since
we know that there is 1 for sure, then we may want to go ahead and start
with trying positive rational roots. I would
suggest
to start with smaller easier numbers and then go from there.
I’m going to choose 1 to try:
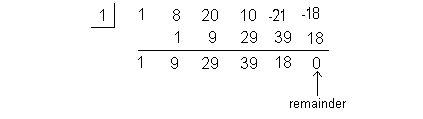
Bingo!!!! We found a number that has a remainder of
0. This means
that x = 1 is a zero or root of our
polynomial
function. |
Use the actual
zero to find
all the zeros:
Since, x = 1 is a zero,
that means x - 1 is a factor of our polynomial function.
Rewriting f(x)
as (x - 1)(quotient) we get:
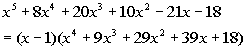
We need to finish this problem by setting this equal
to zero and
solving it: |
Looks like we can’t factor this one. We are going
to have to
repeat this process again, but this time we will use this factor that
we
found.
Recall, that in Descartes’s Rule of Signs we already
found that there
is exactly one positive real zero. It looks like we already found
that, so when we go trying again we can focus on finding a negative
real zero.
Note that we can still pick from the same list of 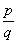 numbers as we did above, since we are still looking at solving the same
overall problem. However when we set up the synthetic division,
we
will just look at the remaining factor, to help us factor that down
farther. numbers as we did above, since we are still looking at solving the same
overall problem. However when we set up the synthetic division,
we
will just look at the remaining factor, to help us factor that down
farther.
I’m going to choose -1 to try:
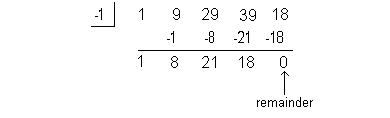
Bingo!!!! We found a number that has a remainder of 0.
This means that x = -1 is a zero or root of our polynomial function. |
Use the actual
zero to find
all the zeros:
Since, x = -1 is a zero,
that means x +1 is a factor of our polynomial function.
Rewriting f(x)
as (x - 1)(x +
1)(quotient) we get:
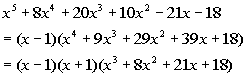
|
Looks like we can’t factor this one. We are going
to have to
repeat this process again, but this time we will use this factor that
we
found.
Recall, that in Descartes’ Rule of Signs we already
found that there
is exactly one positive real zero. It looks like we already found
that, so when we go trying again we can focus on finding a negative
real zero.
Note that we can still pick from the same list of 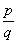 numbers as we did above, since we are still looking at solving the same
overall problem. However when we set up the synthetic division,
we
will just look at the remaining factor, to help us factor that down
farther. numbers as we did above, since we are still looking at solving the same
overall problem. However when we set up the synthetic division,
we
will just look at the remaining factor, to help us factor that down
farther.
I’m going to choose -2 to try:
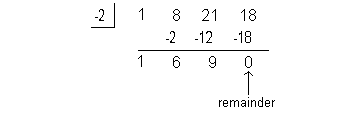
Bingo!!!! We found a number that has a remainder of 0.
This means that x = -2 is a zero or root of our polynomial function. |
Use the actual
zero to find
all the zeros:
Since, x = -2 is a zero,
that means x + 2 is a factor of our polynomial function.
Rewriting f(x)
as (x - 1)(x +
1)(x + 2)(quotient) we get:
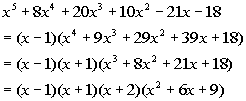
We need to finish this problem by setting this equal
to zero and
solving it: |
|
*Set 1st factor = 0
*Set 2nd factor = 0
*Set 3rd factor = 0
*Set 4th factor = 0
|
The zeros of this function are x = 1,
-1, -2, and -3. |
 Practice Problems Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problem 1a: Use the Rational Zero Theorem
to list all the
possible rational zeros for the given polynomial function. Practice
Problem 1a: Use the Rational Zero Theorem
to list all the
possible rational zeros for the given polynomial function.
 Practice
Problem 2a: Find the possible number of
positive and negative
real zeros of the given polynomial function using Descartes’ Rule of
Signs. Practice
Problem 2a: Find the possible number of
positive and negative
real zeros of the given polynomial function using Descartes’ Rule of
Signs.
 Practice
Problems 3a - 3b: List all of the possible zeros, use
Descartes’ Rule
of Signs to possibly narrow it down, use synthetic division to test the
possible zeros and find an actual zero, and use the actual zero to find
all the zeros of the given polynomial function. Practice
Problems 3a - 3b: List all of the possible zeros, use
Descartes’ Rule
of Signs to possibly narrow it down, use synthetic division to test the
possible zeros and find an actual zero, and use the actual zero to find
all the zeros of the given polynomial function.
 Need Extra Help on these Topics? Need Extra Help on these Topics?
The following are webpages that can assist
you in the topics that were covered on this page:
|

Last revised on March 15, 2012 by Kim Seward.
All contents copyright (C) 2002 - 2012, WTAMU and Kim Seward. All rights reserved.
|
|


