College Algebra
Tutorial 34: Graphs of Quadratic Functions
 Learning Objectives
After completing this tutorial, you should be able to:
- Find the vertex of a quadratic function.
- Determine if the vertex is the maximum or minimum point of a quadratic
function.
- Graph a quadratic function.
|
Introduction
In this tutorial we will be looking at graphs of quadratic functions.
The graph of a quadratic function is called a parabola and has a curved
shape. One of the main points of a parabola is its vertex.
It is the highest or the lowest point on its graph. You can think
of like an endpoint of a parabola. I will be showing you how to find
the vertex as well as the axis of symmetry that goes through this point.
I will also refresh your memory on how to find the x-
and y- intercepts. If you need a review
on what intercepts on a graph are, feel free to go to Tutorial
26: Equations of Lines. When finding x-intercepts,
you will find yourself having to solve a quadratic equation. If you
need a review on solving quadratic equations, feel free to go to Tutorial
17: Quadratic Equations. If you are in a college algebra
class, working with quadratic functions is inevitable, even if it is against
your religion. So I guess you better get started. |
Tutorial
|
Quadratic Function
A quadratic function is a function that
can be written in the form
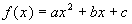
where a, b,
and c
are constants and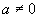 
|
Note that in a quadratic function there is a power of two on your independent
variable and that is the highest power. |
Standard Form of a
Quadratic Function
|
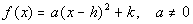
Sometimes your quadratic function is written in standard form.
It is ok to leave it in this form when working with your problem.
I will be showing you how to graph a parabola using either form. |
|
Graph of a Quadratic Function
|
The graph of a quadratic function is called a parabola. It
is basically a curved shape opening up or down. |
When you have a quadratic function in either form, 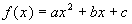OR ,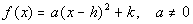
if a > 0, then the parabola opens up  ,
if a < 0, then the parabola opens down  . |
The vertex is the lowest or highest point (depending on direction)
on the graph of a quadratic function.
Finding the vertex using the form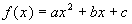
, :
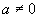If your quadratic function is in the form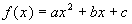
, ,
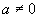then the
vertex = .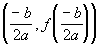
Basically you will find the x value of the
vertex first and then just plug that value into the function to get the y or functional value of the vertex. |
Finding the vertex using the form :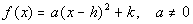
If your quadratic function is in the form ,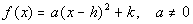
then the
vertex = (h, k).
|
|
Each parabola is symmetric about a vertical line called the axis
of symmetry. This vertical line goes through the vertex.
Think of it as a mirrored image about this vertical line. |
The next three graphs illustrate the different aspects of the graph
of a quadratic function or parabola. |
The following is the graph of the function  :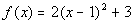
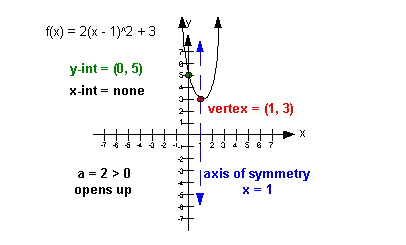
I want you to note a few things about this
graph:
First of all, see how the vertex is the
lowest point on the graph. It is either going to be the lowest or
highest point on the graph of a quadratic function.
Second, look at the axis of symmetry. It is not actually
part of the graph itself, but is important in that the parabola creates
a mirrored image about it. Note how it is symmetric about the axis
of symmetry. Also, note how it goes through the vertex.
Third, note how there is one y-intercept
but no x-intercept. The quadratic
function can have no, one or two x-intercepts. |
|
The following is the graph of the function  :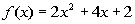
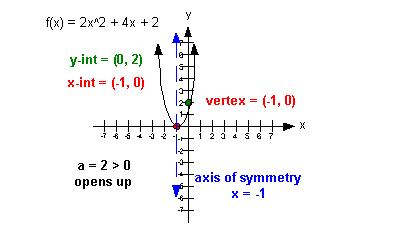
I want you to note a few things about this
graph:
First of all, see how the vertex is the
lowest point on the graph. It is either going to be the lowest or
highest point on the graph of a quadratic function.
Second, look at the axis of symmetry. It is not actually
part of the graph itself, but is important in that the parabola creates
a mirrored image about it. Note how it is symmetric about the axis
of symmetry. Also, note how it goes through the vertex.
Third, note how there is one y-intercept
and one x-intercept. The quadratic
function can have no, one or two x-intercepts. |
|
The following is the graph of the function  :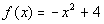
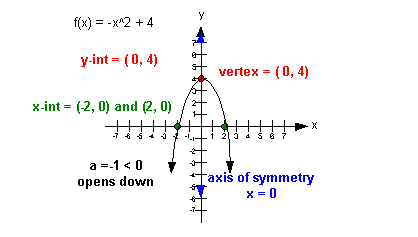
I want you to note a few things about this
graph:
First of all, see how the vertex is the
highest point on the graph. It is either going to be the lowest or
highest point on the graph of a quadratic function.
Second, look at the axis of symmetry. It is not actually
part of the graph itself, but is important in that the parabola creates
a mirrored image about it. Note how it is symmetric about the axis
of symmetry. Also, note how it goes through the vertex.
Third, note how there is one y-intercept
and two x-intercepts. The quadratic
function can have no, one or two x-intercepts. |
|
 Example
1: Find the coordinates of the vertex of  .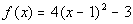
Without graphing, determine if the vertex is the maximum or minimum point
of the quadratic function. |
|
*Standard form of quad. function |
Since (h, k)
is the vertex in standard form, what do you think our vertex is for this
problem?
If you said (1, -3) you are correct.
Be careful about your signs on this problem. It is real tempting
to say that the vertex is (1, 3). However take a close look at the
standard form. Notice how the sign in front of h is a minus, but the one in front of k is positive.
So h is the number we are subtracting from x,
which in our case is 1. k is the number
we are adding at the end, which our case we are adding a negative 3. |
Maximum or Minimum?
Next we want to determine if the vertex that
we found, (1, -3), is a maximum or minimum point, without graphing.
If we know which direction the curve opens, that
can help us answer this question.
Since a = 4, and 4
is greater than 0, this parabola would open up .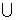
So does that mean the vertex is a maximum or minimum
point?
If you said a minimum point, you are right on.
So our vertex (1, -3) is the minimum point. |
Example
2: Find the coordinates of the vertex of  .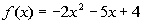
Without graphing, determine if the vertex is the maximum or minimum point
of the quadratic function. |
|
*Identify a, b,
and c
*Plug values into vertex form. for a, b,
and c
*Plug -5/4 in for x to find the y value of the vertex
|
The vertex would be  . |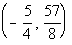
Maximum or Minimum?
Next we want to determine if the vertex that
we found,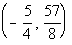 , is a maximum
or minimum point, without graphing.
If we know which direction the curve opens, that
can help us answer this question.
Since a = -2, and
-2 is less than 0, this parabola would open down .
So does that mean the vertex is a maximum or minimum
point?
If you said a maximum point, you are right on.
So our vertex 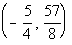is the maximum point. |
|
Graphing a Quadratic Function
|
Step 3: Find the intercepts. |
Step 4: Graph the parabola. |
Plot the points found in steps 2 and 3 and draw a curved line through
them. |
Example
3: Use the vertex and the intercepts to sketch the graph of
the quadratic function  .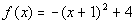
Find the equation for this function's axis of symmetry. |
Since a = -1 and -1 < 0, then it looks
like it is going to curve down.
This gives us a good reference to know we are going in the right direction. |
|
*Standard form of quad. function |
Since (h, k)
is the vertex in standard form, what do you think our vertex is?
If you said (-1, 4) you are correct.
Be careful about your signs on this problem. Notice how
the sign in front of h is a minus, but the
one in front of k is positive. So h is
the number we are subtracting from x, which
in our case is -1. k is the number we
are adding at the end, which our case we are adding a 4. |
y-intercept
Reminder that the y-intercept is always
where the graph crosses the y-axis which means x = 0: |
The y-intercept is (0, 3).
x-intercept
Reminder that the x-intercept is always
where the graph crosses the x-axis which means y = 0: |
The x-intercepts are (-3, 0) and (1,
0). |
Axis of symmetry
As shown on the graph, the axis of symmetry is x = -1. |
Example
4: Use the vertex and the intercepts to sketch the graph of
the quadratic function  .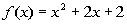
Find the equation for this function's axis of symmetry. |
Since a = 1 and 1 > 0, then it looks like it
is going to curve up.
This gives us a good reference to know we are going in the right direction. |
|
*Identify a, b,
and c
*Plug values into vertex form. for a, b,
and c
*Plug -1 in for x to find the y value of the vertex |
So the vertex is (-1, 1). |
y-intercept
Reminder that the y-intercept is always
where the graph crosses the y-axis which means x = 0: |
The y-intercept is (0, 2).
x-intercept
Reminder that the x-intercept is always
where the graph crosses the x-axis which means y = 0: |
|
*Replace y (or
f(x)) with 0 |
Note that this does not factor. Let's try solving by using
the quadratic formula: |
|
*Plug in values for a, b,
and c
|
Note how we got a negative number underneath the square root.
That means there is no real number solution. That also means that
there are NO x-intercepts. |
Axis of symmetry
As shown on the graph, the axis of symmetry is x = -1. |
Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1b: Find the coordinates of the vertex of the given
quadratic function. Without graphing, determine if the vertex is
the maximum or minimum point of the quadratic function.
Practice
Problems 2a - 2b: Use the vertex and the intercepts to sketch the
graph of the given quadratic function. Find the equation for this
function's axis of symmetry.
Need Extra Help on these Topics?
The following is a webpage that can assist
you in the topics that were covered on this page:
|
Last revised on July 10, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.
|
|
