College Algebra
Answer/Discussion to Practice Problems
Tutorial 32B: Inverse Functions
Let’s look at f(g(x))
first:
|
|
*Insert the
"value" of g inside the function of f
*Plug in the
"value" of g wherever there is an x the function f |
Since BOTH f(g(x))
AND g(f(x)) would have to equal x for them
to be inverses of each other and f(g(x)) is not
equal to x, then we can stop
here and say without a doubt that they are NOT inverses of each
other.
|
Let’s look at f(g(x))
first:
|
|
*Insert the
"value" of g inside the function
of f
*Plug in the
"value" of g wherever there is an x the function f
|
Next, let’s look at g(f(x)): |
|
*Insert the
"value" of f inside the function
of g
*Plug in the
"value" of f wherever there is an x the function g |
Since f(g(x))
AND g(f(x)) BOTH came out to be x, this
proves that the two functions are inverses of each other. |
 Answer/Discussion
to 2a Answer/Discussion
to 2a
|
a) find the equation of 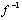 |
Step 1: Replace f(x)
with y.
|
Step 2: Interchange x with y.
|
|
*Inverse of cube root is
cubing both sides
*Inverse of -2 is + 2
|
Since this y is a function, it
is the inverse of the original
function.
|
Step 4: If f has an inverse
function, replace y with 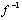 . . |
c)
indicate the domain and range of f and 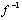 using interval
notation using interval
notation |
The domain of f is
the same as the range of 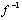 which is 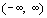 .
The range of f is the same as
the domain of 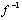 which is which is 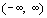 . .
If you need a review on
finding the domain and range of a function, feel free to go to College
Algebra Tutorial
30: Introduction to Functions.
If you need a review on finding the
domain and range of a graph of a function, feel
free to go to College Algebra Tutorial
32: Graphs of Functions, Part II. |
 Answer/Discussion
to 2b Answer/Discussion
to 2b
|
a) find the equation of 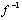 |
Step 1: Replace f(x)
with y.
|
Step 2: Interchange x with y.
|
|
*Inverse of - 2 is + 2
*Inverse of squaring is
to take the square root
|
|
Normally when we take the square root of
both sides, there
are two answers .. the + or – of the square root. But,
because it is only defined for greater than or equal to 0,
then that means we can only use the positive square root.
If we had both + and – in front of the
square root, then
this would not be a function and hence there would not be an inverse.
But, we
do have a function here, so we can carry on …. Since this y is a function, it
is the inverse of the original
function.
|
Step 4: If f has an inverse
function, replace y with 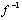 . . |
c)
indicate the domain and range of f and 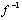 using interval
notation using interval
notation |
The
domain of f is the same as the range of 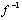 which is 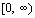 .
The range of f is the same as
the domain of 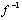 which is which is  . .
If you need a review on
finding the domain and range of a function, feel free to go to College
Algebra Tutorial
30: Introduction to Functions.
If you need a review on finding the
domain and range of a graph of a function, feel
free to go to College Algebra Tutorial
32: Graphs of Functions, Part II. |

Last revised on June 24, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.
|
|


