College Algebra
Tutorial 30B: Operations with Functions
 Learning Objectives Learning Objectives
After completing this tutorial, you should be able to:
- Find the sum of functions.
- Find the difference of functions.
- Find the product of functions.
- Find the quotient of functions.
- Find the composition of functions.
|
 Introduction Introduction
In this tutorial we
will be working with functions. Note as you are
going through this lesson that a lot of the things we are doing we have
done before with expressions. Like adding, subtracting,
multiplying
and dividing. What is new here is we are specifically looking at
these same operations with functions this time. I
think we are ready to forge ahead. |
 Tutorial Tutorial
The following show us how to perform the different
operations
on functions.
Use the functions 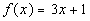 and
and 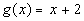 to illustrate the operations:
to illustrate the operations: |
Sum of f + g
(f + g)(x) = f(x) + g(x)
|
This is a very straight forward process. When
you
want the
sum of your functions you simply add the two functions together.
 Example
1: If Example
1: If 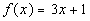 and and 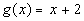 then
find (f + g)(x)
then
find (f + g)(x)
|
|
*Add the 2 functions
*Combine like terms |
Difference of f - g
(f - g)(x) = f(x) - g(x)
|
Another straight forward idea, when you want the
difference of your
functions you simply take the first function minus the second function.
 Example
2: If Example
2: If 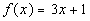 and
and 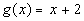 then find (f - g)(x) and (f
- g)(5)
then find (f - g)(x) and (f
- g)(5)
|
|
*Take the difference of the 2
functions
*Subtract EVERY term of the 2nd
( )
*Plug 5 in for x in the diff. of the 2
functions
found above
|
Since the difference function had already been found,
we
didn't have
to take the difference of the two functions again. We could just
merely
plug in 5 into the already found difference function. |
Product of f g
(f g)(x) = f(x)g(x)
|
Along the same idea as adding and subtracting, when
you
want to
find the product of your functions you multiply the functions together.
 Example
3: If Example
3: If 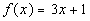 and
and 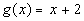 then find (fg)(x)
then find (fg)(x)
|
|
*Take the product of the 2
functions
*FOIL method to multiply
|
Quotient of f/ g
(f /g)(x) = f(x)/g(x)
|
Well, we don't want to leave division of functions out
of the
loop.
It stands to reason that when you want to find the quotient of your
functions you divide the functions.
 Example
4: If Example
4: If 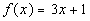 and
and 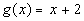 then
find (f/g)(x) and (f/g)(1) then
find (f/g)(x) and (f/g)(1)
|
|
*Write as a quotient of the 2
functions
*Use the quotient found above
to plug
1 in
for x
|
Composite Function
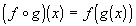
|
|
*g is
inside of f
*Substitute in x + 2 for g
*Plug x +
2 in
for x in function f
|
a) 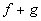
|
Domain:
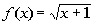 The radicand CANNOT be
negative.
The radicand CANNOT be
negative. In other words it has to be greater than or
equal to zero:
|
|
*Set radicand of x + 1 greater than or equal
to 0 and solve
|
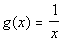 The denominator CANNOT
equal zero:
The denominator CANNOT
equal zero:
|
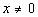
|
*The den. x CANNOT equal zero |
Putting these two sets
together we get the domain:
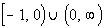
|
b) 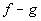
|
|
*Subtract the 2
functions
|
Domain:
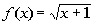 The radicand CANNOT be
negative.
The radicand CANNOT be
negative. In other words it has to be greater than or
equal to zero:
|
|
*Set radicand of x + 1 greater than or equal
to 0 and solve
|
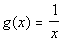 The denominator CANNOT
equal zero:
The denominator CANNOT
equal zero:
|
|
*The den. x CANNOT equal zero |
Putting these two sets
together we get the domain:
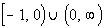
|
c) 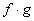
|
|
*Multiply the 2
functions
|
Domain:
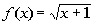 The radicand CANNOT be
negative.
The radicand CANNOT be
negative. In other words it has to be greater than or
equal to zero:
|
|
*Set radicand of x + 1 greater than or equal
to 0 and solve
|
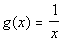 The denominator CANNOT
equal zero:
The denominator CANNOT
equal zero:
|
|
*The den. x CANNOT equal zero |
Putting these two sets
together we get the domain:
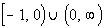
|
d) 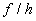
|
Domain:
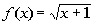 The radicand CANNOT be
negative.
The radicand CANNOT be
negative. In other words it has to be greater than or
equal to zero:
|
|
*Set radicand of x + 1 greater than or equal
to 0 and solve
|
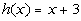 The denominator h(x) CANNOT equal zero:
The denominator h(x) CANNOT equal zero:
|
|
*The den. h(x) = x + 3 CANNOT equal zero |
Putting these two sets
together we get the domain:
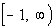
|
e) 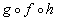
|
|
*h is
inside of f is inside of g
*Substitute in x + 3 for h
*Substitute in sqroot(x + 3 + 1) for f(x + 3)
*Plug sqroot(x + 4) in
for x in function g |
Domain:
The radicand CANNOT be
negative AND the denominator CANNOT equal zero. In other
words it has to be greater than zero:
|
|
*Set radicand of x + 4 greater than 0 and solve
|
The domain would be:
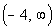
|
 Example 7:
Let f = {(-3, 2),
(-2, 4), (-1, 6), (0, 8)}, and g = {(-2, 5), (0, 7), (2, 9)} and h = {(-3, 0), (-2, 1)}. Find the following functions and state the
domain. Example 7:
Let f = {(-3, 2),
(-2, 4), (-1, 6), (0, 8)}, and g = {(-2, 5), (0, 7), (2, 9)} and h = {(-3, 0), (-2, 1)}. Find the following functions and state the
domain.
a) 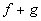 b)
b) 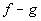 c) c) 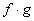 d) d) 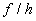 e)
e) 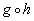
|
a) 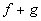
|
When you are looking
for the domain of the sum of two functions that are given as sets, you
are looking for the intersection of their domains.
Since the x values
that f and g have in common are -2 and
0, then the domain would be {-2, 0}.
|
x = -2:
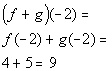 (-2, 9)
(-2, 9)
|
*Add together the corresponding y values to x = -2
|
x = 0:
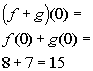 (0, 15)
(0, 15)
|
*Add together the corresponding y values to x = 0
|
Putting it together in
ordered pairs we get:
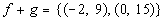
|
b) 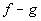
|
When
you are looking for the domain of the difference of two functions that
are
given as sets, you are looking for the intersection of their domains.
Since the x values
that f and g have in common are -2 and
0, then the domain would be {-2, 0}.
|
x = -2:
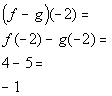 (-2, -1)
(-2, -1)
|
*Subtract the corresponding y values to x = -2
|
x = 0:
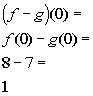 (0, 1)
(0, 1)
|
*Subtract the corresponding y values to x = 0
|
Putting it together in
ordered pairs we get:
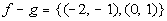
|
c) 
|
When
you are looking for the domain of the product of two functions that are
given as sets, you are looking for the intersection of their domains.
Since the x values
that f and g have in common are -2 and
0, then the domain would be {-2, 0}.
|
x = -2:
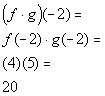 (-2, 20)
(-2, 20)
|
*Multiply the corresponding y values to x = -2
|
x = 0:
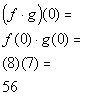 (0, 56)
(0, 56)
|
*Multiply the corresponding y values to x = 0
|
Putting it together in
ordered pairs we get:
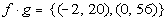
|
d) 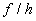
|
When
you are looking for the domain of the quotient of two functions that
are
given as sets, you are looking for the intersection of their domains
AND values of x that do NOT cause the denominator to equal 0.
The x values that f and h have in common are -3 and
-2. However, h(-3) = 0, which would cause the denominator of the
quotient to be 0.
So, the domain would be {-2}.
|
x = -2:
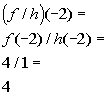 (-2, 4)
(-2, 4)
|
*Find the quotient of the
corresponding y values to x = -2
|
Putting it together in
an ordered pair we get:
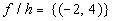
|
e) 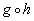 |
When
you are looking for the domain of the composition of two functions that
are
given as sets, you are looking for values that come from the domain of
the inside function AND when you plug those values of x into the inside function, the output is in the domain of the outside
function.
The x values of h are -3 and -2.
However, g(h(-2)) = g(1), which is undefined. In
other words, there are no ordered pairs in g that have a 1 for their x value.
So, the domain would be {-3}.
|
x = -3:
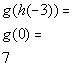 (-3, 7)
(-3, 7)
|
*h(-3) = 0
*Find the y value that
corresponds to x =
0
|
Putting it together in
an ordered pair we get:
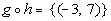
|
When you are writing a
composition function keep in mind that one function is inside of the
other. You just have to figure out which function is the inside
function and which is the outside function.
Note that if you put g inside of f you
would get:
|
Note that if you put f inside of g you would get:
|
Hey this looks familiar.
Our answer is 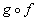 . .
|
 Practice Problems Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1i: If Practice
Problems 1a - 1i: If 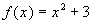 and
and 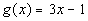 then find the following: then find the following:
 Practice
Problems 2a - 2e: If f = {(1, 2), (2, 3), (3, 4), (4,
5)}, g = {(1, -2), (3,
-3), (5, -5)}, and h = {(1, 0), (2,
1), (3, 2)}, find the following and state the
domain: Practice
Problems 2a - 2e: If f = {(1, 2), (2, 3), (3, 4), (4,
5)}, g = {(1, -2), (3,
-3), (5, -5)}, and h = {(1, 0), (2,
1), (3, 2)}, find the following and state the
domain:
 Practice
Problem 3a: Let Practice
Problem 3a: Let 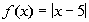 and and 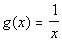 . Write the given function as a
composition function using f and g. . Write the given function as a
composition function using f and g.
 Need Extra Help on these Topics? Need Extra Help on these Topics?

Last revised on March 31, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.
|
|


