College Algebra
Answer/Discussion to Practice Problems
Tutorial 24: Practice Test on Tutorials 14 - 23
Problems 1a - 1c: Solve the given equation and
determine whether
the equation is an identity, a conditional equation or an inconsistent
equation. |
1a. 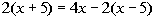
 Answer: Answer:
 Since the variable dropped out AND it is a true
statement, the answer
is all real numbers, which means this equation is an identity. |
1b. 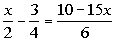
 Answer: Answer:
 Since we came up with the solution x = 29/36,
this would be an example
of a conditional equation. |
1c. 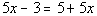
 Answer: Answer:
 Since the variable dropped out AND it is a false
statement, the answer
is no solution which means this is an inconsistent equation. |
Problems 2a - 2b: Solve the given equation. |
|
Note that -2 does not cause any denominators to be
zero. So it
is not an extraneous solution.
-2 is the solution to our equation. |
|
Note that 3 does cause two of the denominators to
be zero.
So 3 is an extraneous solution. That means
there is no solution.
The answer is NO solution. |
Problems 3a - 3c: Solve the given word problem. |
3a. In last week’s football game, Ralph scored 6 less
than twice what
Tommy scored. The sum of their scores is 30. How many
points
did Ralph and Tommy score individually?
 Answer:
Assign variable:
x = Tommy’s
score
2x - 6 = Ralph’s
score Answer:
Assign variable:
x = Tommy’s
score
2x - 6 = Ralph’s
score
Since their sum is 30, we
get the following
equation:
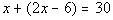
Solving the equation we get:
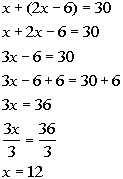
Answer:
Tommy scored 12 points.
Ralph scored 2(12) - 6 = 18 points. |
3b. The ages of three sisters are three even
consecutive integers.
If the sum of the 1st, four times the 2nd, and twice the 3rd is 86,
what
are the three ages?
 Answer:
Assign variable:
x = 1st even consecutive
integer
x + 2 = 2nd even
consecutive integer
x +
4 = 3rd even
consecutive integer Answer:
Assign variable:
x = 1st even consecutive
integer
x + 2 = 2nd even
consecutive integer
x +
4 = 3rd even
consecutive integer
Since the sum of the 1st,
four times the 2nd,
and twice the 3rd is 86, we get the following equation:
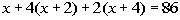
Solving the equation we get:
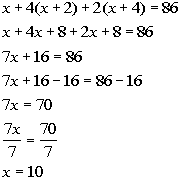
Answer:
The three ages are 10, 12, and 14. |
3c. You are buying a computer at a markdown price
of $960.
If the markdown price was 20% off of the original price, how much was
the computer
originally?
 Answer:
Assign variable:
x = original price Answer:
Assign variable:
x = original price
Since the markdown price
is $960, we get the
following equation:
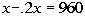
Solving the equation we get:
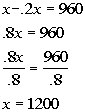
Answer:
The original price of the computer is $1200. |
Problem 4a: Solve for the given variable. |
Problems 5a - 5b: Solve the given equation by
factoring. |
|
There are two solutions to this equation: x = -2 and x = 7. |
|
There are two solutions to this equation: x = -1/2 and x = -2/3. |
Problems 6a - 6b: Solve the given equation by
completing the
square. |
|
There are two solutions to this equation: x = -1 + 2i and x =
-1 - 2i. |
|
There are two solutions to this equation: x = 7/4 + 1/4 = 2 and x = 7/4 - 1/4 = 6/4
= 3/2
. |
Problems 7a - 7b: Solve the given equation by
using the quadratic
equation. |
7b. 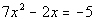
 Answer: Answer:
Write in standard form:
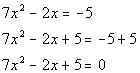
Put in quadratic formula:
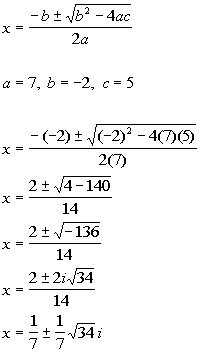 |
Problems 8a - 8b: Solve the given equation by
factoring. |
|
There are three solutions to this equation: a = 0, a = -3, and a = 3. |
|
There are three solutions to this equation: x = 5, x = -2, and x = 2. |
Problems 9a - 9b: Solve the given equation. |
|
Checking for extraneous solutions:
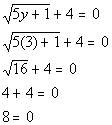
Since we got a false statement, y = 3 is
an extraneous solution.
This means there is no solution to this
equation. |
|
Both x = -1 and x = 3 check.
There are two solutions to this equation: x = -1 and x = 3. |
Problem 10a: Solve the given equation. |
|
a = 8 does check.
There is one solution to this equation: a = 8. |
Problems 11a - 11b: Solve the given equation. |
11a. 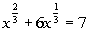
 Answer: Answer:
Writing the equation in standard form:
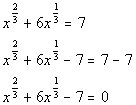
Substitution:
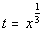
Substitute in t and
solve:
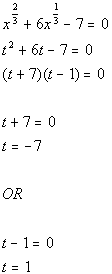
Substitute value in for t and solve for x:
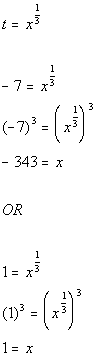
There are two solutions to this equation: x = -343 and x = 1. |
11b. 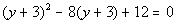
 Answer: Answer:
Substitution:
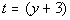
Substitute in t and
solve:
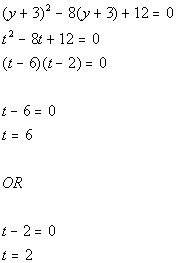
Substitute value in for t and solve for y:
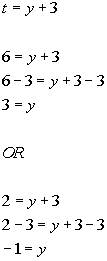
There are two solutions to this equation: y = 3 and y = -1. |
Problems 12a - 12b: Solve the given equation. |
12a. 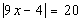
 Answer: Answer: First solution:
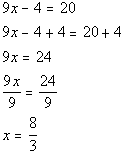
Second solution:
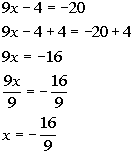
There are two solutions to this equation: x = 8/3 and x = -16/9. |
12b. 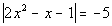
 Answer: Answer:
Since the absolute value
is set equal to a
negative number, there is no solution. |
Problems 13a - 13b: Solve, write your answer
in interval notation
and graph the solution set. |
|
Interval notation: 
Graph:
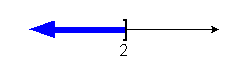 |
|
Interval notation: 
Graph:
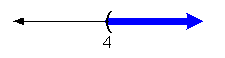 |
Problems 14a - 14d: Solve, write your answer
in interval notation
and graph the solution set. |
14a. 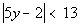
 Answer: Answer:
Use the definition of absolute value to set up:
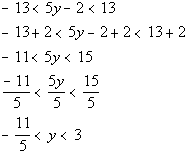
Interval notation: 
Graph:
 |
14b. 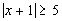
 Answer: Answer:
Use the definition of absolute value to set up:
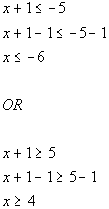
Interval notation: 
Graph:
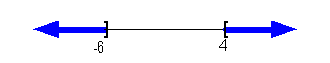 |
14c. 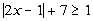
 Answer: Answer:
Isolate the absolute
value:
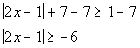
Since the absolute value is ALWAYS positive and in
this problem it is
set greater than or equal to a negative number, the answer is all
real
numbers. |
14d. 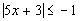
 Answer: Answer:
Since the absolute value is ALWAYS positive and in
this problem it is
set less than a negative number, the answer is no solution. |
Problems 15a - 15b: Solve, write your answer
in interval notation
and graph the solution set. |
15a. 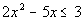
 Answer: Answer:
Write in standard form:
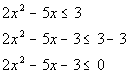
Solve quadratic equation:
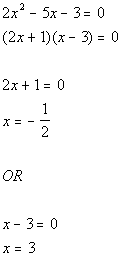
Mark off boundary points on number line:

Note that the two boundary points create three sections on the
graph:  , , 
 . .
Chose -1 in first interval to check:
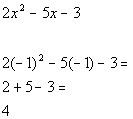
Since 4 is positive and we are looking for values
that cause our quadratic
expression to be less than or equal to 0 (negative or 0),  would
not be part of the solution. would
not be part of the solution.
Chose 0 in second interval to check:
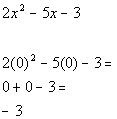
Since -3 is negative and we are looking for values
that cause our expression
to be less than or equal to 0 (negative or 0),  would be part of the solution. would be part of the solution.
Chose 4 in third interval to check:
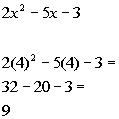
Since 9 is positive and we are looking for values
that cause our quadratic
expression to be less than or equal to 0 (negative or 0),  would
not be part of the solution. would
not be part of the solution.
Interval notation: 
Graph:
 |
15b. 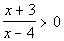
 Answer: Answer:
Set numerator equal to 0 and solve:
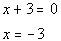
Set denominator equal to 0 and solve:
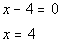
Mark off boundary points on number line:

Note that the two boundary points create three sections on the
graph:  , ,  ,
and ,
and  . .
Chose -4 in first interval to check:
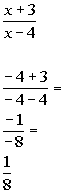
Since 1/8 is positive and we are looking for
values that cause our quadratic
expression to be greater than 0 (positive),  would
be part of the solution. would
be part of the solution.
Chose 0 in second interval to check:
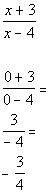
Since -3/4 is negative and we are looking for
values that cause our
quadratic expression to be greater than 0 (positive),  would
not be part of the solution. would
not be part of the solution.
Chose 5 in third interval to check:
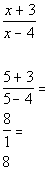
Since 8 is positive and we are looking for values
that cause our quadratic
expression to be greater than 0 (positive),  would
be part of the solution. would
be part of the solution.
Interval notation: 
Graph:
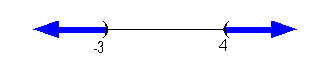 |

Last revised on Jan. 15, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward.
All rights reserved.
|
|


