College Algebra
Tutorial 22: Linear Inequalities
WTAMU > Virtual Math Lab > College Algebra
 Learning Objectives
After completing this tutorial, you should be able to:
- Use the addition, subtraction, multiplication, and division properties
of inequalities to solve linear inequalities.
- Solve linear inequalities involving absolute values.
- Write the answer to an inequality using interval notation.
- Draw a graph to give a visual answer to an inequality problem.
|
Introduction
In this tutorial we will be looking at solving linear
inequalities.
When solving linear inequalities, we use a lot of the same concepts
that
we use when solving linear equations (shown in Tutorial
14: Linear Equations in One Variable). Basically, we
still
want to get the variable on one side and everything else on the other
side
by using inverse operations. The difference is, when a variable
is
set equal to one number, that number is the only solution. But,
when
a variable is less than or greater than a number, there are an infinite
number of values that would be a part of the answer. We will also
revisit the definition of absolute value and how it applies to
inequalities.
If you need a review on absolute values go to Tutorial
21: Absolute Value Equations. You never know when
you
will need to know about inequalities, so you better get started. |
Tutorial
Read left to right:
a < b a is less than b
a < b a is less than or equal to b
a > b a is greater than b
a > b a is
greater than or equal to b |
Interval notation is a way to notate the range of
values that would
make an inequality true. There are two types of intervals, open
and
closed (described below), each with a specific way to notate it so we
can
tell the difference between the two.
Note that in the interval notations (found below), you
will see the
symbol  ,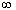
which
means infinity.
Positive infinity (  )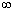
means it goes on and on indefinitely to the right of the number - there
is no endpoint on the right.
Negative infinity (-)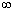
means it goes on and on indefinitely to the left of the number - there
is no endpoint to the left.
Since we don’t know what the largest or smallest
numbers are, we need
to use infinity or negative infinity to indicate there is no endpoint
in
one direction or the other. |
In general, when using interval notation, you always put
the smaller
value of the interval first (on the left side), put a comma between the
two ends, then put the larger value of the interval (on the right
side).
You will either use a curved end ( or ) or a boxed end [ or ],
depending
on the type of interval (described below).
If you have either infinity or negative infinity on
either end, you
always use a curve for that end. This will indicate that there is no
definite
endpoint in that direction, it keeps going and going. |
An open interval does not include where your
variable is equal to
the endpoint.
To indicate this, we use a curved end as shown
below. |
|
Inequality
|
Interval Notation for
Open Intervals
|
|
x > a |
( a, ) |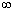
|
x < a |
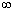(- , a) |
|
When you graph an open ended end point, you use the
same curved end
( or ) on the graph as you do in the interval
notation.
Also, darken in the part of the graph that is the solution. For
example, |
|
Inequality
|
Interval Notation for
Open Intervals
|
Graph
|
|
x > 4
|
(4, )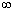
|
|
|
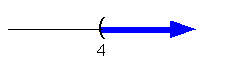
x 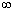< 4
|
(-, 4)
|
|
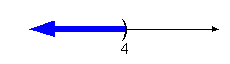
A closed interval includes where your variable is
equal to the endpoint.
To indicate this, we use a boxed end as shown
below.
As mentioned above, even though a is
included
and has a boxed end, if it goes to either infinity or negative infinity
on the other end, we will notate it with a curved end for that end only! |
|
Inequality
|
Interval Notation for
Closed Intervals
|
|
x > a |
[a, )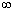
|
|
x < a |
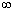(- , a] |
|
When you graph a closed ended end point, you use the
same boxed end
[ or ] on the graph as you do in the interval
notation.
Also, darken in the part of the graph that is the solution. For
example, |
|
Inequality
|
Interval Notation for
Closed Intervals
|
Graph
|
|
x > 4
|
[4, )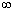
|
|
|
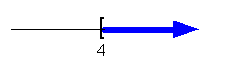
x < 4
|
(-, 4]
|
|
|
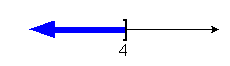
Combining Open and Closed
Intervals
|
Sometimes one end of your interval is open and the
other end is closed.
You still follow the basic ideas described above. The closed end
will have a [ or ] on it’s end and the open end will have a
( or ) on its end. |
|
Interval Notation for
Combining Open and
Closed Intervals
|
|
a < x < b |
(a, b] |
|
a < x < b |
[a, b) |
|
|
Inequality
|
Interval Notation for
Combining Open and
Closed Intervals
|
Graph
|
|
3 < x < 6
|
[3, 6)
|
|
|
Addition/Subtraction Property
for Inequalities
If a < b, then a + c < b + c
If a < b, then a - c < b - c
|
In other words, adding or
subtracting the
same expression to both sides of an inequality does not change the
inequality.
 Example
1: Solve, write your answer in interval notation and
graph
the solution set:  .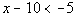
 View a video of this example
|
|
Interval notation: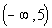
Graph:
 |
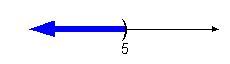*Inv. of sub. 10 is add. 10
*Open interval indicating all
values less than
5
*Visual showing all numbers
less than 5 on
the number line
|
Note that the inequality stayed the same throughout the
problem.
Adding or subtracting the same value to both sides does not change the
inequality.
The answer 'x is less than
5' means that
if we put any number less than 5 back in the original problem, it would
be a solution (the left side would be less than the right side).
As mentioned above, this means that we have more than just one number
for
our solution, there are an infinite number of values that would satisfy
this inequality.
Interval notation:
We have an open interval since we are not including where it is equal
to 5. x is less than
5, so
5 is the largest value of the interval, so it goes on the right.
Since there is no lower endpoint (it is ALL values less than 5), we put
the negative infinity symbol on the left side. The curved end on
5 indicates an open interval. Negative infinity always has a
curved
end because there is not an endpoint on that side.
Graph:
We use the same type of notation on the endpoint as we did in the
interval
notation, a curved end. Since we needed to indicate all
values
less than 5, the part of the number line that was to the left of 5 was
darkened. |
|
Interval notation: [-3, )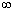
Graph:
 |
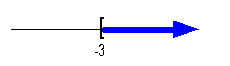*Inv. of add 4 is sub. 4
*Closed interval indicating all
values greater
than or = -3
*Visual showing all numbers
greater than or
= to -3 on the number line.
|
Note that the inequality stayed the same throughout the
problem.
Adding or subtracting the same value to both sides does not change the
inequality.
The answer 'x is greater
than or equal to
-3' means that if we put any number greater than or equal to -3 back in
the original problem, it would be a solution (the left side would be
greater
than or equal to the right side). As mentioned above, this means
that we have more than just one number for our solution, there are an
infinite
number of values that would satisfy this inequality.
Interval notation:
We have a closed interval since we are including where it is equal
to -3. x is greater than or
equal
to -3, so -3 is our smallest value of the interval, so it goes on the
left.
Since there is no upper endpoint (it is ALL values greater than or
equal
to -3), we put the infinity symbol on the right side. The boxed
end
on -3 indicates a closed interval. Infinity always has a curved
end
because there is not an endpoint on that side.
Graph:
We use the same type of notation on the endpoint as we did in the
interval
notation, a boxed end. Since we needed to indicate
all
values greater than or equal to -3, the part of the number line that
was
to the right of -3 was darkened. |
Multiplication/Division
Properties for Inequalities
when multiplying/dividing by a positive value
If a < b AND c is positive, then ac < bc
If a < b AND c is positive, then a/c < b/c
|
In other words, multiplying
or dividing the
same POSITIVE number to both sides of an inequality does not change the
inequality.
Example
3: Solve, write your answer in interval notation and
graph
the solution set:  .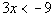
View a video of this example
|
|
Interval notation: (-,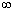
-3)
Graph:
 |
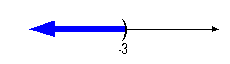*Inv. of mult. by 3 is div. by 3
*Open interval indicating all
values less than
-3
*Visual showing all numbers
less than -3 on
the number line
|
Note that the inequality sign stayed the same
direction. Even
though the right side was a -9, the number we were dividing both sides
by, was a positive 3. Multiplying or dividing both sides by
the
same positive value does not change the inequality.
Interval notation:
We have an open interval since there we are not including where it
is equal to -3. x is less
than
-3, so -3 is our largest value of the interval, so it goes on the
right.
Since there is no lower endpoint (it is ALL values less than -3), we
put
the negative infinity symbol on the left side. The curved end on
-3 indicates an open interval. Negative infinity always has a
curved
end because there is not an endpoint on that side.
Graph:
We use the same type of notation on the endpoint as we did in the
interval
notation, a curved end. Since we needed to indicate all
values
less than -3, the part of the number line that was to the left of -3
was
darkened. |
Multiplication/Division
Properties for Inequalities
when multiplying/dividing by a negative value
If a < b AND c
is negative, then ac > bc
If a < b AND c
is negative, then a/c > b/c
|
In other words, multiplying
or dividing the
same NEGATIVE number to both sides of an inequality reverses the sign
of
the inequality.
The reason for this is, when you multiply or divide an
expression by
a negative number, it changes the sign of that expression. On the
number line, the positive values go in a reverse or opposite direction
than the negative numbers go, so when we take the opposite of an
expression,
we need to reverse our inequality to indicate this.
|
|
Interval notation: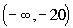 
Graph:
 |
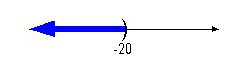*Inv. of div. by -4 is mult.
by -4, so reverse inequality sign
*Open interval indicating all
values less than
-20
*Visual showing all numbers
less than -20 on
the number line
|
I multiplied by a -4 to take care of both the negative
and the division
by 4 in one step.
In line 2, note that when I did
show the step
of multiplying both sides by a -4, I reversed my inequality sign.
Interval notation:
We have an open interval since we are not including where it is equal
to -20. x is less than
-20,
so -20 is our largest value of the interval, so it goes on the
right.
Since there is no lower endpoint (it is ALL values less than -20), we
put
the negative infinity symbol on the left side. The curved end on
-20 indicates an open interval. Negative infinity always has a
curved
end because there is not an endpoint on that side.
Graph:
We use the same type of notation on the endpoint as we did in the
interval
notation, a curved end. Since we needed to indicate all
values
less than -20, the part of the number line that was to the left of -20
was darkened. |
|
Interval notation: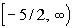 
Graph:
 |
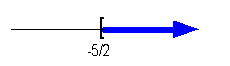*Inv. of mult. by -2 is div.
by -2, so reverse inequality sign
*Closed interval indicating all
values greater
than or = -5/2
*Visual showing all numbers
greater than or
= -5/2 on the number line
|
In line 2, note that when I
did show the step
of dividing both sides by a -2, that I reversed my inequality sign.
Interval notation:
We have a closed interval since we are including where it is equal
to -5/2. x is greater than
or equal
to -5/2, so -5/2 is our smallest value of the interval so it goes on
the
left. Since there is no upper endpoint (it is ALL values greater
than or equal to -5/2), we put the infinity symbol on the right
side.
The boxed end on -5/2 indicates a closed interval. Infinity
always
has a curved end because there is not an endpoint on that side.
Graph:
We use the same type of notation on the endpoint as we did in the
interval
notation, a boxed end. Since we needed to indicate
all
values greater than or equal to -5/2, the part of the number line that
was to the right of -5/2 was darkened. |
|
Strategy for Solving a Linear
Inequality
|
Step 1:
Simplify
each side if needed.
This would involve things like removing ( ),
removing fractions, adding
like terms, etc. |
Step 2:
Use Add./Sub.
Properties to move the variable term on one side and all other terms to
the other side.
Step 3: Use Mult./Div.
Properties to remove any values that are in front of the variable.
Note that it is the same basic
concept we used
when solving linear equations as shown in Tutorial
14: Linear Equations in One Variable.
|
|
Interval notation: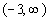
Graph:
 |
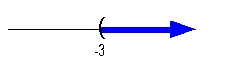*Inv. of add. 5 is sub. 5
*Inv. of mult. by -2 is div.
both sides by
-2, so reverse inequality sign
*Open interval indicating all
values greater
than -3
*Visual showing all numbers
greater than -3
on the number line
|
Interval notation:
We have an open interval since we are not including where it is equal
to -3. x is greater than -3,
so
-3 is our smallest value of the interval so it goes on the left.
Since there is no upper endpoint (it is ALL values less than -3), we
put
the infinity symbol on the right side. The curved end on -3
indicates
an open interval. Infinity always has a curved end because there
is not an endpoint on that side. Graph:
We use the same type of notation on the endpoint as we did in the
interval
notation, a curved end. Since we needed to indicate all
values
greater than -3, the part of the number line that was to the right of
-3
was darkened. |
|
Interval notation: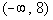
Graph:
 |
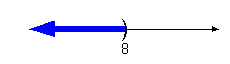*Distributive property
*Get x terms on
one side, constants on the other side
*Inv. of sub. 3 is add. by 3
*Open interval indicating all
values less than
-1/2
*Visual showing all numbers
less than -1/2
on the number line. |
Interval notation:
Again, we have an open interval since we are not including where it
is equal to 8. This time x is less than 8, so 8 is our largest value of the interval so it
goes
on the right. Since there is no lower endpoint (it is ALL values
less than 8), we put the negative infinity symbol on the left
side.
The curved end on 8 indicates an open interval. Negative infinity
always has a curved end because there is not an endpoint on that side. Graph:
Again, we use the same type of notation on the endpoint as we did in
the interval notation, a curved end. Since we needed to indicate
all values less than 8, the part of the number line that was to the
left
of 8 was darkened. |
|
Interval notation: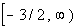
Graph:
 |
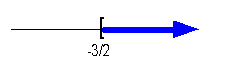*Mult. both sides by LCD of 6
*Get x terms on
one side, constants on the other side
*Inv. of add. 3 is sub. by 3
*Inv. of mult. by 10 is div. by
10
*Closed interval indicating all
values greater
than or equal to -3/2
*Visual showing all numbers
greater than or
equal to -3/2 on the number line. |
Interval notation:
This time we have a closed interval since we are including where it
is equal to -3/2. x is
greater
than or equal to -3/2, so -3/2 is our smallest value of the interval so
it goes on the left. Since there is no upper endpoint (it is ALL
values greater than or equal to -3/2), we put the infinity symbol on
the
right side. The boxed end on -3/2 indicates a closed
interval.
Infinity always has a curved end because there is not an endpoint on
that
side. Graph:
Again, we use the same type of notation on the endpoint as we did in
the interval notation, a boxed end this time. Since we
needed
to indicate all values greater than or equal to -3/2, the part of the
number
line that was to the right of -3/2 was darkened. |
|
Solving a Compound
Inequality
|
A compound linear inequality is one that has two
inequalities in
one problem. For example, 5 < x + 3 < 10 or -1 < 3 x < 5.
You
solve them exactly the same way you solve the
linear
inequalities shown above, except you do the steps to three
"sides"
(or parts) instead of only two. |
This is an example of an compound inequality |
|
Interval notation: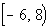
Graph:
 |
*Inv. of add. 2 is sub. by 2
*Apply steps to all three
parts
*All values between -6 and 8,
with a closed
interval at -6 (including -6)
*Visual showing all numbers
between -6 and
8, including -6 on the number line. |
Interval notation:
This time we have a mixed interval since we are including where it
is equal to -6, but not equal to 8. x is between -6 and 8, including -6, so -6 is our smallest value of the
interval
so it goes on the left and 8 goes on the right. The boxed
end
on -6 indicates a closed interval on that side. A curved end on 8
indicates
an open interval on that side.
Graph:
Again, we use the same type of notation on the endpoints as we did
in the interval notation, a boxed end on the left and a curved
end
on the right. Since we needed to indicate all values between -6
and
8, including -6, the part of the number line that is in between -6 and
8 was darkened. |
|
Solving an Absolute Value
Inequality
|
Step 1: Isolate
the absolute value expression. |
If there is a constant that is on the same side of the
inequality that
the absolute value expression is but is not inside the absolute value,
use inverse operations to isolate the absolute value. |
Step 2: Use the
definition of absolute value to set up the inequality without absolute
values. |
A quick reminder, the absolute value measures the
DISTANCE a number
is away from the origin (zero) on the number line. No matter if
the
number is to the left (negative) or right (positive) of zero on the
number
line, the DISTANCE it is away from zero is going to be positive. Hence,
the absolute value is always positive, (or zero if you are taking the
absolute
value of 0).
If you need a review on absolute values, feel free to go
to Tutorial
21: Absolute Value Equations. |
|
If d is POSITIVE
and |x|
< d, then
-d < x < d
The graph below illustrates all the values on the number
line whose
distance would be less than d units away
from
0. It shows us why we set up the inequality, shown above, the way
we do.
|
If d is NEGATIVE
and |x|
< d, then
there is no solution
The absolute value is always positive, and any positive
number is greater
than any negative number, therefore it would be no solution.
|
|
If d is
POSITIVE and |x| > d, then
x < -d
OR x > d
The graph, shown below, illustrates all the values on
the number line
whose distance would be greater than d units
away from 0. It shows us why we set up the inequality, shown
above,
the way we do.
|
If d is NEGATIVE
and |x|
> d, then
x is all real numbers
The absolute value is always positive, and any positive
number is greater
than any negative number, therefore all real numbers would work.
|
You will solve these linear inequalities just like the
ones shown above. |
The absolute value expression is already isolated. |
The distance that the expression x - 4
is away from the origin needs to be less than 7.
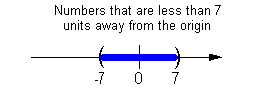
All numbers between -7 and 7 are less than 7 units away
from the origin.
So, the expression x - 4 needs to be
between
-7 and 7. |
|
Interval notation: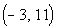
Graph:
 |
*Inv. of sub. 4 is add. by 4
*Apply steps to all three parts
*All values between -3 and 11
*Visual showing all numbers
between -3 and
11
|
Interval notation:
This time we have an open interval since we are not including either
endpoint. x is between -3 and 11,
so
-3 is our smallest value of the interval so it goes on the left and 11
goes on the right. The curved end on both numbers indicate
an open interval on both sides.
Graph:
Again, we use the same type of notation on the endpoints as we did
in the interval notation, a curved end on both ends. Since
we needed to indicate all values between -3 and 11, the part of
the
number line that is in between -3 and 11 was darkened. |
The absolute value expression is already isolated. |
Be careful, since the absolute value (the left side) is
always positive,
and positive values are always greater than negative values, the answer
is no solution. There is no value that we can put in for x that would make this inequality true. |
|
*Inv. of add. 1 is sub. 1
*Abs. value exp. isolated
|
The distance that the expression (7
- 2y)/2
is away from the origin needs to be greater than or equal to 4.
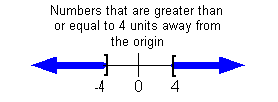
All numbers that are less than or equal to - 4 OR
greater than or equal
to 4 are greater than or equal to 4 units away from the origin.
So
the expression (7 - 2y)/2 needs to be
less
than or equal to - 4 OR greater than or equal to 4. |
|
OR
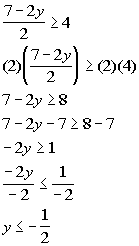
Interval notation: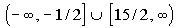
Graph:
 |
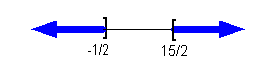*First inequality, where it is
less than or
= to -4
*Inv. of div. by 2 is mult. by 2
*Inv. of mult. by -2 is div. by
-2, so reverse inequality sign
*Second inequality, where it is
greater than
or = to 4
*Inv. of div. by 2 is mult. by 2
*Inv. of mult. by -2 is div. by
-2, so reverse inequality signs
*All values less than or = to
-1/2 or greater
than or = to 15/2
*Visual showing all numbers
less than or =
to -1/2 or greater than or = to 15/2 |
Interval notation:
This time we have two closed intervals since we are including the
endpoints
-1/2 and 15/2.
In the first interval, y is less than or
equal to -1/2, so -1/2 is our largest value of the interval so it goes
on the right. Since there is no lower endpoint of that first
interval,
we put negative infinity on the left side. The boxed end on -1/2
indicates a closed interval. Infinity always has a curved end
because
there is not an endpoint on that side.
In the second, interval, y is greater
than or equal to 15/2, so 15/2 is our smallest value of the interval so
it goes on the left. Since there is no upper endpoint of that
second
interval, we put the infinity symbol on the right side. The boxed
end on 15/2 indicates a closed interval. Infinity always has a
curved
end because there is not an endpoint on that side.
Graph:
Again, we use the same type of notation on the endpoints as we did
in the interval notation, a boxed end on both y = -1/2 and y = 15/2. Since we
needed
to indicate all values less than or equal to -1/2 OR greater than or
equal
to 15/2, the parts of the number line that are to the left of -1/2 and
to the right of 15/2 were darkened. |
The absolute value expression is already isolated. |
Again, be careful - since the absolute value (the left
side) is always
positive, and positive values are always greater than negative values, the
answer is all real numbers. No matter what value you plug in
for x, when you take the absolute value
the
left side will be positive. All positive numbers are greater than
-2. |
Practice Problems
These are practice problems to help bring you to the
next level.
It will allow you to check and see if you have an understanding of
these
types of problems. Math works just like
anything
else, if you want to get good at it, then you need to practice
it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the
problem out on
your own and then check your answer by clicking on the link for the
answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1c: Solve, write your answer in interval
notation and graph
the solution set.
Practice
Problems 2a - 2d: Solve, write your answer in interval
notation and graph
the solution set.
Need Extra Help on these Topics?
Videos at this site were created and produced by Kim Seward and Virginia Williams Trice.
Last revised on Dec. 17, 2009 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward.
All rights reserved.
|
|
.
.
.
.
.
.
.
.
.
.
.
