College Algebra
Answer/Discussion to Practice Problems
Tutorial 16: Formulas and Applications
WTAMU > Virtual Math Lab > College Algebra > Tutorial 16: Formulas and Applications
 Answer/Discussion
to 1a Answer/Discussion
to 1a
In last night’s basketball game, Sally scored 9 less
than twice what
Lucy scored. The sum of their scores is 27. How many points
did Sally and Lucy make individually? |
Make sure that you read the question carefully several
times.
We are looking for two numbers, and since we can write
the number of
points Sally made in terms of the number of points Lucy scored we will
let
x = the number of
points Lucy scored
Sally scored 9 less than twice what Lucy scored:
2x - 9 = number of
points Sally scored
|
|
*Combine like terms
*Inv. of sub. 9 is add. 9
*Inv. of mult. by 3 is div. by 3
|
If we add 12 and a 15 (a number 9 less than twice 12)
we do get 27.
FINAL ANSWER:
The number of points Lucy scored was 12.
The number of points Sally scored was 15. |
 Answer/Discussion
to 1b Answer/Discussion
to 1b
The heights in inches of three basketball players are 3
consecutive
integers. If the sum of twice the 1st, 3 times the 2nd, and the
3rd
is 437, what are the three heights. |
Make sure that you read the question carefully several
times.
We are looking for 3 consecutive
integers, we will let
x = 1st consecutive
integer
x + 1 = 2nd consecutive
integer
x + 2 = 3rd
consecutive integer
|
|
*Remove ( ) by using dist. prop.
*Combine like terms
*Inv. of add. 5 is sub. 5
*Inv. of mult. by 6 is div. by 6
|
If we take the sum of twice 72, three times 73, and 74,
we do get 437
FINAL ANSWER:
The heights of the three basketball players in inches
are 72, 73,
and 74.
|
 Answer/Discussion
to 1c Answer/Discussion
to 1c
A rectangular floor has a perimeter of 54 feet. If
the length
is 3 more than the width, what are the dimensions of the floor? |
Make sure that you read the question carefully several
times.
We are looking for the length and width of the
rectangle. Since
length can be written in terms of width, we will let
w = width
length is 3 feet more than the width:
w + 3 = length
|
|
*Remove ( ) by using dist. prop.
*Combine like terms
*Inv. of sub. 6 is add. 6
*Inv. of mult. by 4 is div. by 4
|
If width is 12, then length, which is 3 feet more than
the width, would
have to be 15. The perimeter of a rectangle with width of 12 feet
and length of 15 feet does come out to be 54.
FINAL ANSWER:
Width is 12 feet.
Length is 15 feet. |
 Answer/Discussion
to 1d Answer/Discussion
to 1d
The original price of a CD player was marked down 15%
and is now $127.50, how much was the original price?
|
Make sure that you read the question carefully several
times.
We are looking for the price of the CD player before the
markdown, we
will let
x = price of the CD
player before the
markdown.
|
|
*Combine like terms
*Inv of mult. .85 is div. by .85
|
If you markdown 15% from $150 you would get $127.50.
FINAL ANSWER:
The original price is $150.
|
 Answer/Discussion
to 2a Answer/Discussion
to 2a
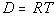 for T for T
|
In this problem, we need to solve for T.
This means we need to get T on one side
and
EVERYTHING ELSE on the other side using inverse operations.
Let’s solve this formula for T: |
|
*Inverse of mult. by R is div. by R
*Formula solved for T
|
 Answer/Discussion
to 2b Answer/Discussion
to 2b
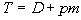 for m for m
|
In this problem, we need to solve for m.
This means we need to get m on one side
and
EVERYTHING ELSE on the other side using inverse operations.
Let’s solve this formula for m: |
|
*Inverse of add. by D is sub. by D
*Inverse of mult. by p is div. by p
*Formula solved for m
|

WTAMU > Virtual Math Lab > College Algebra > Tutorial 16: Formulas and Applications
Last revised on Dec. 15, 2009 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward.
All rights reserved.
|
|


