Title
West Texas A&M University - Home
Virtual Math Lab

College Algebra
Tutorial 10: Adding and Subtracting Rational Expressions

 

deskLearning Objectives

After completing this tutorial, you should be able to:
  1. Find the least common denominator of rational expressions.
  2. Add and subtract rational expressions.




deskIntroduction


Do you ever feel dazed and confused when working with fractions?  If so, you are not alone.  This is your lucky day!  We have a whole other tutorial devoted to rational expressions (fractions).  In this tutorial we will be looking at adding and subtracting them.  If you need a review on simplifying rational expressions, feel free to go back to Tutorial 8: Simplifying Rational Expressions.  It is time to get started with this tutorial.

 

 

desk Tutorial


 

Adding or Subtracting Rational Expressions 
with Common Denominators

add

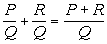
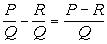
subtract


 
Step 1: Combine the numerators together.

 

Step 2: Put the sum or difference found in step 1 over the common denominator.

 

Step 3: Reduce to lowest terms as shown in Tutorial 8: Simplifying Rational Expressions.

 
 
 
Why do we have to have a common denominator
when we add or subtract rational expressions?????

 
Good question.  The denominator indicates what type of fraction that you have and the numerator is counting up how many of that type you have.  You can only directly combine fractions that are of the same type (have the same denominator).  For example if 2 was my denominator, I would be counting up how many halves I had.  If 3 was my denominator, I would be counting up how many thirds I had.  But I would not be able to add a fraction with a denominator of 2 directly with a fraction that had a denominator of 3 because they are not the same type of fraction.  I would have to find a common denominator first, which we will cover after the next two examples.

 
 
 

notebook Example 1:  Add example 1a.

videoView a video of this example

 
Since the two denominators are the same, we can go right into adding these two rational expressions.

 
Step 1: Combine the numerators together

AND

Step 2: Put the sum or difference found in step 1 over the common denominator.

 
example 1b
*Common denominator of 5x - 2
 
 

*Combine the numerators
*Write over common denominator
 
 
 
 

*Excluded values of the original den.

 
Step 3: Reduce to lowest terms.

 
Note that neither the numerator nor the denominator will factor.  The rational expression is as simplified as it gets.

Also note that the value that would be excluded from the domain is 2/5.  This is the value that makes the original denominator equal to 0.

 
 
 

notebook Example 2:  Subtract example 2a.

videoView a video of this example

 
Since the two denominators are the same, we can go right into subtracting these two rational expressions.

 
Step 1: Combine the numerators together

AND

Step 2: Put the sum or difference found in step 1 over the common denominator.

 
example 2b

*Common denominator of y - 1
 

*Combine the numerators
*Write over common denominator
 

 
Step 3: Reduce to lowest terms.

 
example 2c
 
 

*Factor the num.

*Simplify by div. out the common factor of (y - 1)
 
 
 
 
 
 

*Excluded values of the original den.

 
Note that the value that would be excluded from the domain is 1.  This is the value that makes the original denominator equal to 0.

 


 

Least Common Denominator (LCD)

 
Step 1: Factor all the denominators
 
 
If you need a review on factoring, feel free to go back to Tutorial 7: Factoring Polynomials.

 

Step 2: The LCD is the list of all the DIFFERENT factors in the denominators raised to the highest power that there is of each factor.


 
 

Adding and Subtracting Rational Expressions 
Without a Common Denominator

 
Step 1: Find the LCD as shown above if needed.

 

Step 2: Write equivalent fractions using the LCD if needed.

 
If we multiply the numerator and denominator by the exact same expression it is the same as multiplying it by the number 1.  If that is the case,  we will have equivalent expressions when we do this. 

Now the question is WHAT do we multiply top and bottom by to get what we want?  We need to have the LCD, so you look to see what factor(s) are missing from the original denominator that is in the LCD.  If there are any missing factors then that is what you need to multiply the numerator AND denominator by.

 

Step 3: Combine the rational expressions as shown above.

 

Step 4: Reduce to lowest terms as shown in Tutorial 8: Simplifying Rational Expressions.

 
 
 

notebook Example 3:  Add example 3a.

videoView a video of this example

 
Step 1: Find the LCD as shown above if needed.

 
The first denominator has the following two factors:

 
example 3b
*Factor the GCF

 
The second denominator has the following factor:

 
example 3c

 
Putting all the different factors together and using the highest exponent, we get the following LCD:

 
example 3d

 
Step 2: Write equivalent fractions using the LCD if needed.

 
Since the first rational expression already has the LCD, we do not need to change this fraction.

 
example 3e
 

*Rewriting denominator in factored form

 

 
Rewriting the second expression with the LCD:

 
example 3f

*Missing the factor of (y - 4) in the den.

*Mult. top and bottom by (y - 4)

 

 
Step 3: Combine the rational expressions as shown above.

 
example 3g
 
 

*Combine the numerators
*Write over common denominator
 
 

 

 
Step 4: Reduce to lowest terms. 

 
example 3h
 
 

*Simplify by div. out the common factor of y
 
 

*Excluded values of the original den.

 
Note that the values that would be excluded from the domain are 0 and 4.  These are the values that make the original denominator equal to 0.

 
 
 

notebook Example 4:  Add example 4a.

videoView a video of this example

 
Step 1: Find the LCD as shown above if needed.

 
The first denominator has the following factor:

 
example 4b

 
The second denominator has the following two factors:

 
example 4c

 
Putting all the different factors together and using the highest exponent, we get the following LCD:

 
example 4d

 
Step 2: Write equivalent fractions using the LCD if needed.

 
Rewriting the first expression with the LCD:

 
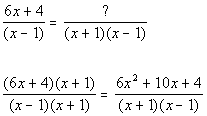example 4e
 

*Missing the factor of (x + 1) in the den.
*Mult. top and bottom by (x + 1)

 

 
Since the second rational expression already has the LCD, we do not need to change this fraction.

 
example 4f
*Rewriting denominator in factored form

 

 
 
Step 3: Combine the rational expressions as shown above.

 
example 4g

*Combine the numerators
*Write over common denominator
 
 
 
 
 
 
 

*Excluded values of the original den.

 
Step 4: Reduce to lowest terms. 

 
This rational expression cannot be simplified down any farther. 

 
Also note that the values that would be excluded from the domain are -1 and 1.  These are the values that make the original denominator equal to 0.

 
 
 

notebook Example 5:  Subtract example 5a.

videoView a video of this example

 
Step 1: Find the LCD as shown above if needed.

 
The first denominator has the following two factors:

 
example 5b
*Factor the trinomial

 
The second denominator has the following two factors:

 
example 5c
*Factor the trinomial

 
Putting all the different factors together and using the highest exponent, we get the following LCD:

 
example 5d

 
Step 2: Write equivalent fractions using the LCD if needed.

 
Rewriting the first expression with the LCD:

 
example 5e
 

*Missing the factor of (x - 8) in the den.
*Mult. top and bottom by (x - 8)

 

 
Rewriting the second expression with the LCD:

 
example 5f
 

*Missing the factor of (x + 5) in the den.
*Mult. top and bottom by (x + 5)

 

 
 
Step 3: Combine the rational expressions as shown above.

 
example 5g2

*Combine the numerators
*Write over common denominator
 

*Distribute the minus sign through the (   )
 
 

 

 
Step 4: Reduce to lowest terms. 

 
example 5h
*Factor the num.

*No common factors to divide out
 

*Excluded values of the original den.

 
Note that the values that would be excluded from the domain are -5,  -1 and 8.  These are the values that make the original denominator equal to 0.

 

 

desk Practice Problems


These are practice problems to help bring you to the next level.  It will allow you to check and see if you have an understanding of these types of problems. Math works just like anything else, if you want to get good at it, then you need to practice it.  Even the best athletes and musicians had help along the way and lots of practice, practice, practice, to get good at their sport or instrument.  In fact there is no such thing as too much practice.

To get the most out of these, you should work the problem out on your own and then check your answer by clicking on the link for the answer/discussion for that  problem.  At the link you will find the answer as well as any steps that went into finding that answer.

 

pencil Practice Problems 1a - 1b: Perform the indicated operation.


 

 

 

desk Need Extra Help on these Topics?


The following are webpages that can assist you in the topics that were covered on this page:
 
http://www.wtamu.edu/academic/anns/mps/math/mathlab/int_algebra/int_alg_tut33_addrat.htm
This webpage will help you with adding and subtracting rational expressions.

http://www.purplemath.com/modules/rtnladd.htm
This webpage goes over finding the least common denominator and combining rational expressions.

 

Go to Get Help Outside the Classroom found in Tutorial 1: How to Succeed in a Math Class for some more suggestions.

 

buffalo top

 


Videos at this site were created and produced by Kim Seward and Virginia Williams Trice.
Last revised on Dec. 15, 2009 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.