Beginning Algebra
Tutorial 14: Solving Linear Equations

WTAMU > Virtual Math Lab > Beginning Algebra

Learning Objectives

After completing this tutorial, you should be able to:

Solve linear equations by using a combination of simplifying and using various properties of equality.

Introduction

In Tutorial 12: The Addition Property of Equality we looked at using the addition property of equality to help us solve linear equations. In Tutorial 13: The Multiplication Property of Equality we looked at using the multiplication property of equality and also put these two ideas together. In this tutorial we will be solving linear equations by using a combination of simplifying and various properties of equality.

Knowing how to solve linear equations will open the door to being able to work a lot of other types of problems that you will encounter in your various algebra classes. It is very important to have this concept down before moving ahead. Make sure that you do not savor the mystery of finding your variable, but work through some of these types of problems until you have this concept down.

Tutorial

Strategy for Solving a Linear Equation

Note that your teacher or the book you are using may have worded these steps a little differently than I do, but it all boils down to the same concept - get your variable on one side and everything else on the other using inverse operations.

Step 1: Simplify each side, if needed.

This would involve things like removing ( ), removing fractions, removing decimals, and adding like terms.

To remove ( ): Just use the distributive property found in Tutorial 8: Properties of Real Numbers.

To remove fractions: Since fractions are another way to write division, and the inverse of divide is to multiply, you remove fractions by multiplying both sides by the LCD of all of your fractions. If you need a review on the LCD, go to Tutorial 3: Fractions.

Step 2: Use Add./Sub. Properties to move the variable term to one side and all other terms to the other side.

Step 3: Use Mult./Div. Properties to remove any values that are in front of the variable.

Step 4: Check your answer.

I find this is the quickest and easiest way to approach linear equations.

Example 1: Solve the equation .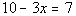

*Inverse of add. 10 is sub. 10

*Inverse of mult. by -3 is div. by -3

Be careful going from line 4 to line 5. Yes, there is a negative sign. But, the operation between the -3 and x is multiplication not subtraction. So if you were to add 3 to both sides you would have ended up with -3x + 3 instead of the desired x.

If you put 1 back in for x in the original problem you will see that 1 is the solution we are looking for.

Example 2: Solve the equation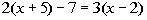

*Remove ( ) by using dist. prop.

*Get all x terms on one side

*Inverse of add. 3 is sub. 3

*Inverse of mult. by -1 is div. by -1

If you put 9 back in for x in the original problem you will see that 9 is the solution we are looking for.

Example 3: Solve the equation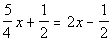

*To get rid of the fractions,
mult. both sides by the LCD of 4

*Get all the x terms on one side

*Inverse of add. 2 is sub. 2

*Inverse of mult. by -3 is div. by -3

If you put 4/3 back in for x in the original problem you will see that 4/3 is the solution we are looking for.

Example 4: Solve the equation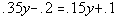

*To get rid of the decimals,
mult. both sides by 100

*Get all the y terms on one side

*Inverse of sub. 20 is add 20

*Inverse of mult. by 20 is div. by 20

If you put 3/2 back in for y in the original problem you will see that 3/2 is the solution we are looking for.

Contradiction

A contradiction is an equation with one variable that has no solution.

Example 5: Solve the equation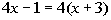

*Remove ( ) by using dist. prop.

*Get all the x terms on one side

Where did our variable, x, go??? It disappeared on us. Also note how we ended up with a FALSE statement, -1 is not equal to 12. This does not mean that x = 12 or x = -1.

Whenever your variable drops out AND you end up with a false statement, then after all of your hard work, there is NO SOLUTION.

So, the answer is no solution.

Identity

An identity is an equation with one variable
that has all numbers as a solution.

Example 6: Solve the equation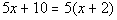

*Remove ( ) by using dist. prop.

*Get all the x terms on one side

This time when our variable dropped out, we ended up with a TRUE statement. Whenever that happens your answer is ALL REAL NUMBERS.

So, the answer is all real numbers.

Practice Problems

These are practice problems to help bring you to the next level. It will allow you to check and see if you have an understanding of these types of problems. Math works just like anything else, if you want to get good at it, then you need to practice it. Even the best athletes and musicians had help along the way and lots of practice, practice, practice, to get good at their sport or instrument. In fact there is no such thing as too much practice.

To get the most out of these, you should work the problem out on your own and then check your answer by clicking on the link for the answer/discussion for that problem. At the link you will find the answer as well as any steps that went into finding that answer.