College Algebra
Tutorial 9: Multiplying and Dividing Rational Expressions
 Learning Objectives
After completing this tutorial, you should be able to:
- Multiply rational expressions.
- Divide rational expressions.
|
Introduction
In this tutorial I will be stepping you through how to multiply and
divide rational expressions. A lot of times in math you are having
to use past concepts to be able to work all the way through the new problems.
In this section you will have to remember how to factor, simplify rational
expressions and multiply polynomials to be able to complete the multiplication
or division problems. If you need a review on multiplying polynomials,
feel free to go back to Tutorial 6:
Polynomials. If you need a review on factoring, feel free
to go back to Tutorial 7: Factoring
Polynomials. If you need a review on simplifying rational
fractions, feel free to go back to Tutorial
8: Simplifying Rational Expressions. I think that you
are ready to move ahead. |
Tutorial
|
Multiplying Rational Expressions
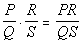
Q and S do not equal 0.
|
Step 1: Factor both the
numerator and the denominator. |
Step 2: Write as one
fraction. |
Write it as a product of the factors of the numerators over the product
of the factors of the denominators. DO NOT multiply anything out
at this point. |
Step 3: Simplify the
rational expression. |
Step 4: Multiply any
remaining factors in the numerator and/or denominator. |
Step 1: Factor both the
numerator and the denominator
AND |
Step 2: Write as one
fraction. |
Step 3: Simplify the
rational expression.
AND |
Step 4: Multiply any
remaining factors in the numerator and/or denominator. |
|
*Simplify by div. out the common factors of (y + 3),
(y - 3) and y
*Excluded values of the original den. |
Note that even though all of the factors in the numerator were divided
out there is still a 1 in there. It is easy to think there there
is "nothing" left and make the numerator disappear. But when you
divide a factor by itself there is actually a 1 there. Just like
2/2 = 1 or 5/5 = 1.
Also note that the values that would be excluded from the domain
are 0, 3, -6, and -3. Those are the values that makes the
original denominator equal to 0. |
Step 1: Factor both the
numerator and the denominator
AND |
Step 2: Write as one
fraction. |
Step 3: Simplify the
rational expression.
AND |
Step 4: Multiply any
remaining factors in the numerator and/or denominator. |
|
*Simplify by div. out the common factors of
(x - 3), 2, and
(x + 2)
*Excluded values of the original den. |
Note that the values that would be excluded from the domain are
0, 3, and -2. Those are the values that makes the original
denominator equal to 0. |
|
Dividing Rational Expressions
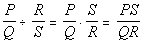
where Q, S, and R do not equal 0.
|
|
*Rewrite as mult. of reciprocal
*Factor the num. and den.
*Simplify by
div. out the common factors of
3x and (x + 6)
*Multiply the den. out
*Excluded values of the original den. of product |
In the numerator of the product we factored a GCF.
In the denominator we factored a trinomial. |
Note that the values that would be excluded from the domain are
-6 and 0. Those are the values that makes the original denominator
of the product equal to 0. |
|
*Rewrite as mult. of reciprocal
*Factor the num. and den.
*Simplifyby
div. out the common factors of
y, (y + 4), and (y - 4)
*Multiply the num. and den. out
*Excluded values of the original den. of quotient
& product |
Note that the values that would be excluded from the domain are
0, 2, - 4, 4, and -3. Those are the values that make the original
denominator of the quotient and the product equal to 0. |
Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1b: Perform the indicated operation.
Need Extra Help on these Topics?
WTAMU > Virtual Math Lab > College Algebra
Videos at this site were created and produced by Kim Seward and Virginia Williams Trice.
Last revised on Dec. 14, 2009 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.
|
|
Example
1: Multiply 
.
.
.
.
