College Algebra
Tutorial 54A: Sequences
 Learning Objectives
After completing this tutorial, you should be able to:
- Know what a sequence, term, nth term, arithmetic
sequence, geometric sequence, Fibonacci sequence, finite sequence,
infinite sequence, and recursive formula are.
- Evaluate any term of a finite sequence.
- Evaluate any term of an infinite sequence.
- Evaluate a factorial.
- Write a formula of a given sequence.
- Work with a recursive formula.
|
Introduction
In this tutorial we will mainly be going over
sequences. We will start by going through some basic terminology
associated with sequences. Arithmetic and geometric sequences are
special forms that are touched on lightly here, but are looked at more
in depth in Tutorial 54C: Arithmetic Sequences and Series and Tutorial
54D: Geometric Sequences and Series. We will be
looking at
sequences forwards and backwards. In some cases, you will be
given the formula for the nth
term, and you will need to come up with the term and in other cases you
are shown the pattern of the terms in the sequence and you will need to
come up with the formula. Once you are able to go back and forth,
then that means you have sequences down. Enough chit chat, let's
get started. |
Tutorial
In general, a sequence
is an ordered arrangement of numbers, figures, or objects.
Sequences of math are a string of numbers that are
tied together with some sort of consistent rule, or set of rules, that
determines the next number in the sequence.
|
The terms of a
sequence are the output values or dependent variables. |
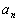 represents
the nth term of a sequence.
a represents the functional or output value and n represents the input value
of term number.
For example, 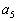 represents the
fifth term of the sequence.
|
An arithmetic sequence
is a sequence such that each successive term is obtained from the
previous term by addition or subtraction of a fixed number called a
difference.
The sequence 4, 7, 10, 13, 16, ... is an example of
an arithmetic sequence - the pattern is that we are always adding a
fixed number of three to the previous term to get to the next term.
Be careful that you don't think that every sequence that has a pattern
in addition is arithmetic. It is arithmetic if you are always adding
the SAME number each time.
For a more in depth look at arithmetic sequences,
feel free to go to Tutorial 54C: Arithmetic Sequences and Series.
|
A geometric sequence
is a sequence such that each successive term is obtained from the
previous term by multiplying by a fixed number called a ratio.
The sequence 5, 10, 20, 40, 80, .... is an example
of a geometric sequence. The pattern is that we are always
multiplying by a fixed number of 2 to the previous term to get to the
next term.
Be careful that you don't think that every sequence that has a pattern
in multiplication is geometric. It is geometric if you are always
multiplying by the SAME number each time.
For a more in depth look at geometric sequences, feel free to go to
Tutorial 54D: Geometric Sequences and Series. |
A basic Fibonacci
sequence is when two numbers are added together to get the next number
in the sequence.
1, 1, 2, 3, 5, 8, 13, .... is an example of a
Fibonacci sequence where the starting numbers (or seeds) are 1 and 1,
and we add the two previous numbers to get the next number in the
sequence. |
A finite sequence is a
sequence whose domain consists of the set {1, 2, 3, ... n} or in other words the
first n positive integers. |
An infinite sequence
is a sequence whose domain consists of the set {1, 2, 3, ...} or in
other words all positive integers. |
The factorial symbol is the exclamation point: !
So if I wanted to write 7 factorial it would be written
as 7!.
In general, n! = n(n - 1)(n -
2)(n - 3)...(1)
Most, (if not all), of you will have a factorial key on your
calculator.
It looks like this: !
If you have a graphing calculator, it will be hidden
under the MATH
menu screen and then select your Probability screen - there you should
find !
0! Has a special
definition attached
with it. 0! = 1 |
 Example
1: Find all of the terms of the finite sequence 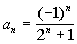 , 1 < n < 5
|
Basically, to find the nth term of a sequence works
in the same fashion as function notation. If you want to find the
3rd term, you are looking for 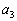 , which means you
plug in 3 for n into the given function.
So, what are we going to plug in for n to find the 1st term?
If you said 1, give yourself a pat on the back. What about the
2nd term? I hope you said you would plug in 2 for n.
Since we have to go from 1 < n < 5, this means we need
to find 5 terms and we will be plugging in 1, 2, 3, 4, and 5 for n.
Let's see what we get:
|
Note how we had -1 raised to n, which changes value, and
the signs of the terms alternated.
The five terms of this
sequence are -1/3, 1/5, -1/9, 1/17, and -1/33.
|
Example 2: Find
the first six terms and the fifteenth term of the infinite sequence
with the nth term
of  .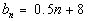
|
Note how there is no bound for n like there was in example
1. This means the sequence goes on and on or in other words it is
an infinite
sequence. We still approach finding terms the same way
we did in example 1. n is our term number and we plug the term number into the function to
find the value of the term.
Let's see what we get for
our first six terms:
|
The first six terms
are 8, 8.5, 9, 9.5, 10, 10.5, and 11.
Note how each term went up by 0. 5 from the previous
term.
Now let's check out the fifteenth term:
|
The fifteenth term is
15.5.
|
Example 3: Find
the first six terms and the tenth term of the infinite sequence with
the nth term of  .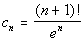
|
This function contains a factorial.
Let's see what we get for our first six terms:
|
Now let's check out
the tenth term:
|
Example 4: Write
a formula for the nth term of
the infinite sequence  .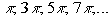
|
Let's take a look at
what is happening here:
When n = 1,
the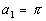n 
n = 2,
the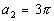n 
n = 3,
the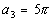n 
n = 4,
then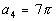 
an so forth.
Something
that is always constant is that each term contains  .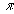
It also looks like it goes up by odd numbers starting with 1. What we need to do
is to think about what the relationship between n and the odd number
(the part that changes) is:
When n is 1, the odd number is 1.
When n is 2, the
odd number is 3.
When n is 3, the odd number is
5.
When n is 4, the
odd number is 7. |
What
do you think the relationship is?
It looks like the number is always one less than twice n. In other words, the number
is 2 n - 1.
So the formula for the nth term is  .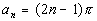
Sometimes you have to play around with it before you get it just
right. You can always check it by putting in the n values and seeing if you
get the given sequence. This one does check.
|
Example 5: Write
a formula for the nth term of
the infinite sequence -1, 8, -27, 64, ....
|
Let's take a look at
what is happening here:
This time there isn’t anything constant, but there are two things that
change.
First
let's look at the alternating signs:
For it to have
alternating signs, we need to have (-1) raised to a power that
changes. This means n,
the term number is involved.
The first term is negative, the second term is positive, the third
negative, the fourth positive and so forth.
When n is odd (1,
3, 5, ...), then the term is negative.
When n is even (2,
4, 6, ...), then the term is positive.
So do you think we are going to have 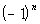 or  .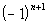
If you said 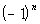you are
correct!!! If n is odd, then this term will be negative. If n is even, then this term
will be positive.
|
Forgetting about the
negative signs for a moment, we also have 1, 8, 27, 64.
Again
we need to figure out the relationship between n and the term itself:
When n is 1, the number is 1.
When n is 2, the
number is 8.
When n is 3, the number is 27.
When n is 4, the
number is 64.
|
What
do you think the relationship is?
It looks like the number is always n cubed.
Putting it together, the
formula for the nth term is  .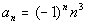
Sometimes you have to play around with it before you get it just
right. You can always check it by putting in the n values and seeing if you
get the given sequence.
This one does check.
|
In a recursive
formula, the nth term of the
sequence is a function of or has a relationship with the previous term.
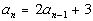 is an example of a recursive
formula, because in order to get the nth
term you need to take 2 times the term before it and then add 3. |
Example 6: Find
the first three terms and the fifth term of the infinite sequence given
by the recursive formula  .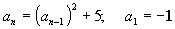
|
We are giving the first term, 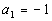 . Using that we can find the
second term and so forth.
Let's see what we get for
our first three terms:
|
Since this is a
recursive formula, in order to the fifth term, we need to find the
fourth term:
|
Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice.
To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice Problem 1a: Find all of
the terms of the finite sequence.
Practice Problem 2a: Find the
first five terms and the twelfth term of the infinite sequence.
Practice Problem 3a: Write a formula for
the nth term of
given the infinite sequence.
Practice Problem 4a: Find the
first three terms and the fifth term of the infinite sequence given by
the recursive formula.
Need Extra Help on these Topics?
Last revised on May 16, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.
|
|
; 1 
; 