College Algebra
Tutorial 47: Exponential Growth and Decay
 Learning Objectives Learning Objectives
After completing this tutorial, you should be able to:
- Solve exponential growth problems.
- Solve exponential decay problems.
|
 Introduction Introduction
In this tutorial I will step you through how to solve
problems that deal in exponential growth and decay. These
problems
will require you to know how to evaluate exponential expressions and
solve exponential equations.
If you need a review on these topics, feel free to go
to Tutorial
42: Exponential Functions and Tutorial
45: Exponential Equations. Ready, set, GO!!!!! |
 Tutorial Tutorial
Exponential Growth
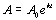 , (k > 0)
, (k > 0)
|
A represents the amount at a given time t.
Ao represents the initial amount of the
growing entity. Note that this is the amount when t = 0.
k is a constant that represents the growth rate. It is POSITIVE
when talking in terms of exponential GROWTH.
t is the amount of time that has past.
If the information for time is given in dates, you need to convert it
to how much time has past since the initial time. For example, if
the model is set up at an initial year of 2000 and you need to find out
what the value is in the year 2010, t would be 2010 - 2000 = 10
years.
You can use this formula to find any of its variables, depending on the
information given and what is being asked in a problem. For
example, you may be given the values for Ao and t and you need to find the amount A after the given time. Or, you may be given the final amount A and the initial amount Ao and you need to find the time t.
Some examples of exponential growth are population growth and financial
growth. The information found, can help predict what a population
for a city or colony would be in the future or what the value of your
house is in ten years. Or you can use it to find out how long it
would take to get to a certain population or value on your house.
The diagram below shows exponential growth:
|
 Example
1 Example
1: The exponential growth model 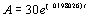 describes the
population of a city in the United States, in thousands, t years after
1994. Use this model to solve the following:
A) What was the population of the city in 1994?
B) By what % is the population of the city increasing each year?
C) What will the population of the city be in 2005?
D) When will the city’s population be 60 thousand?
|
A) What was the population of the city in 1994? |
Since we are looking for the population, what variable
are we seeking? If you said A you are right on!!!!
The way the problem is worded, 1994 is what we call our initial
year. This is when t = 0.
Plugging in 0 for t and solving for A we get:
|
|
*Replace t with 0
*e^0 simplifies to be 1
|
When writing up the final answer, keep in mind that the
problem said that the population was in thousands.
The population in 1994 would be 30,000.
Another way that we could have approached this problem was noting that
the year was 1994, which is our initial year, so basically it was
asking us for the initial population, which is Ao in the
formula. This happens to be the number in front of e which is 30 in this problem.
The reason I showed you using the formula was to get you use to
it. Just note that when it is the initial year, t is 0,
so you will have e raised to the 0 power which means it will
simplify to be 1 and you are left with whatever Ao is.
|
B) By what % is the population of the city
increasing
each year? |
As mentioned above, in the general growth formula, k is a constant that represents the growth rate. k is the
coefficient of t in e’s exponent.
So what would be our answer in terms of percent?
Well, k = .0198026, so converting that to percent we get 1.98026%
for our answer.
|
C) What will the population of the city be in 2005? |
Since we are looking for the population, what variable
are we finding? If you said A give yourself a high five.
What are we going to plug in for t in this problem?
Our initial year is 1994, and since t represents years after
1994, we can get t from 2005 - 1994, which would be 11.
Plugging in 11 for t and solving for A we get:
|
|
*Replace t with 11
*e^ .2178286 is
approx. 1.243373935
|
Again, when writing up the final answer, keep in mind
that the problem said that the population was in thousands.
The population in 2005 would be approximately 37, 301.
|
D) When will the city’s population be 60 thousand? |
Looks like we have a little twist here. Now we
are given the population and we need to first find t to find
out how many years after 1994 we are talking about and then convert
that knowledge into the actual year.
We will still be using the same formula we did to answer the questions
above, we will just be using it to find a different variable.
Plugging in 60 for A and solving for t we get:
|
This means a little over 35 years after 1994, the
population will be 60 thousand.
So our answer is during the year 2029.
|
 Example 2 Example 2: A house is purchased for $150,000 in
2002. The value of the house is given by the exponential growth model 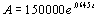 . Find
when the house would be worth $200,000.
|
Since we are looking for when, what variable do we
need to find? If you said t give yourself a high
five.
What are we going to plug in for A in this problem? If
you said 200000, you are correct!
Plugging 200000 for A in the model we get:
|
Rounding 4.46 to the nearest whole number we get t = 4.
Since t is measured in years since 2002, the model indicates
that the population will reach 200000 in year 2002 + 4 = 2006.
|
Exponential Decay
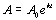 , (k < 0)
, (k < 0)
|
A represents the amount at a given time t.
Ao represents the initial amount of the
growing entity. Note that this is the amount when t = 0.
k is a constant that represents the growth rate. It is NEGATIVE
when talking in terms of exponential DECAY.
t is the amount of time that has past.
If the
information for time is given in dates, you need to convert it to how
much time has past since the initial time. For example, if the
model
is set up at an initial year of 2000 and you need to find out what the
value is in the year 2010, t would be 2010 - 2000 = 10 years.
You can use this formula to find any of its variables, depending on the
information given and what is being asked in a problem. For
example,
you may be given the values for Ao and t and you need to find the amount A after the given time. Or, you may be given the final amount A and the initial amount Ao and you need to find the time t.
Examples of exponential decay are radioactive decay and population
decrease. The information found can help predict what the
half-life of a radioactive material is or what the population will be
for a city or colony in the future. The
half-life of a given substance is the time required for half of that
substance to decay or disintegrate.
The diagram below shows exponential decay:
|
 Example 3 Example 3: An artifact originally had 12 grams
of carbon-14 present. The decay model 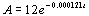 describes the
amount of carbon-14 present after t years. How many grams of
carbon-14 will be present in this artifact after 10,000 years?
|
If we are looking for the number of grams of carbon-14
present, what variable do we need to find? If you said A give
yourself a high five.
What are we going to plug in for t in this problem?
Since t represents the number of years, it looks like we will
be plugging in 10,000 for t.
Plugging in 10000 for t and solving for A we get:
|
There will be approximately 3.58 grams of carbon-14
present after 10,000 years.
|
 Example 4 Example 4: A certain radioactive isotope element
decays exponentially according to the model 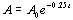 , where A is the
number of grams of the isotope at the end of t days and Ao is the
number of grams present initially. What is the half-life of this
isotope?
|
If we are looking for the half-life of this isotope,
what variable are we seeking? If you said t you are
correct!!!!
It looks like we don’t have any values to plug into A or Ao.
However, the problem did say that we were interested in the HALF-life,
which would mean ½ of the initial amount (Ao) would be
present at the end (A) of that time. This means A can be
replaced with .5Ao.
Replacing A with .5 Ao and solving for t we get:
|
The half-life of this isotope is approximately 2.77
days.
|
 Example 5 Example 5: Prehistoric cave paintings were
discovered in a cave in Egypt. The paint contained 20% of the
original carbon-14. Using the exponential decay model for
carbon-14, 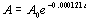 , estimate the age of the paintings.
|
Since we are looking for the age of the paintings, what
variable are we looking for? If you said t you are
correct!!!!
It looks like we don’t have any values to plug into A or Ao.
However, the problem did say that the paintings that were found
contained 20% of the original carbon-14. This means A can
be replaced with .2Ao (20% of the original).
Replacing A with .2 Ao and solving for t we get:
|
The age of the paintings are approximately 13301
years.
|
 Practice Problems Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice.
To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice Problems 1a - 1b: Solve the given exponential
growth or decay problem. Practice Problems 1a - 1b: Solve the given exponential
growth or decay problem.
1a. The value of the property in a particular
block follows a pattern of exponential growth. In the year 2001,
your company purchased a piece of property in this block. The
value of the property in thousands of dollars, t years after 2001 is
given by the exponential growth model 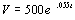 .
Use this model to solve the following:
A) What did your company pay for the property?
B) By what percentage is the price of the property in this block
increasing per year?
C) What will the property be worth in the year 2010?
D) When will the property be worth 750 thousand dollars?
(answer/discussion
to 1a) |
1b. An artifact originally had 10 grams of carbon-14
present. The decay model 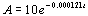 describes the
amount of carbon-14 present after t years.
Use this model to solve the following:
A) How many grams of carbon-14 will be present in this artifact after
25,000 years?
B) What is the half-life of carbon-14?
(answer/discussion
to 1b) |
 Need Extra Help on these Topics? Need Extra Help on these Topics?

Last revised on March 25, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.
|
|


