College Algebra
Tutorial 27: Graphing Lines
 Learning Objectives
After completing this tutorial, you should be able to:
- Graph a straight line using the y-intercept
and slope.
- Graph vertical and horizontal lines.
|
Introduction
In this tutorial we will be looking at graphing lines. There
are several ways that you can approach graphing a line. We will be
looking specifically at using the y-intercept
and slope to help us get our straight line. I will provide a review
on slope as well as the slope/intercept form of a line as we go through
this lesson. If you need more review on these concepts, feel free
to go to Tutorial 25: Slope of a Line and Tutorial 26: Equations of Lines.
The concept of graphing vertical and horizontal lines will also be covered
on this page. Basically, we will plot the y-intercept
point and then use the slope to find a second point and then connect the
dots to get your graph. |
Tutorial
Here is a little review on what the slope of a line tells about
that line. If you need more of a review on slope, feel free to
go to Tutorial 25: Slope of a Line. |
The slope of a line measures the steepness of the line.
Most of you are probably familiar with associating slope with "rise
over run".
Rise means how many units you move up or down from point to
point. On the graph that would be a change in the y values.
Run means how far left or right you move from point to point.
On the graph, that would mean a change of x values. |
Here are some visuals to help you with this definition:
Positive slope:
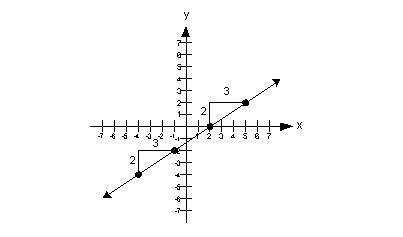
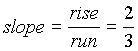
Note that when a line has a positive slope it goes up left to right. |
| Negative slope:
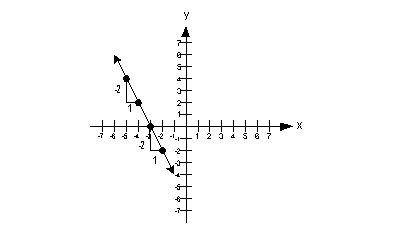
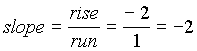
Note that when a line has a negative slope it goes down left to right. |
| Zero slope:
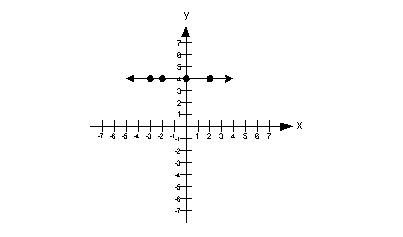
slope = 0
Note that when a line is horizontal the slope is 0. |
| Undefined slope:
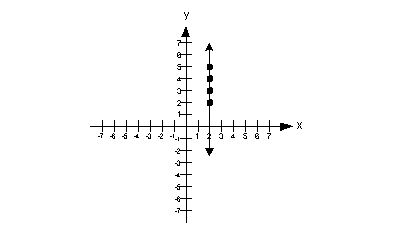
slope = undefined
Note that when the line is vertical the slope is undefined. |
Here is a little review on the slope/intercept form of the equation
of a line. If you need more of a review on slope, feel free to
go to Tutorial 26: Equations of Lines. |
|
Slope/Intercept Equation of a Line
|
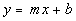
If your linear equation is written in this form, m represents the slope and b represents the y-intercept.
This form can be handy if you need to find the slope of a line given
the equation. |
|
Graphing a Line Using the y-intercept and
Slope
|
Step 1: Put
the equation in slope/intercept form ()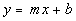
and identify the slope and y-intercept. |
When it is in this form it makes it easier to identify the slope and
the y-intercept of the line.
In this form, the slope is m, which is the
coefficient in front of x and the y-intercept
is the constant b. |
Step 2: Plot
the y-intercept on a 2-dimensional graph. |
Recall that the y-intercept is where it
crosses the y-axis. So x's
value will be 0.
If you need more review on intercepts, feel free to go to Tutorial
26: Equations of Lines. |
Step 3: Use
the slope to find a second point on the line. |
You will start with the y-intercept and
rise up or down and then run left or right depending on the sign of the
slope.
Use the concept of slope being rise over run (rise/run) to determine
how to use the slope to find your second point.
What do you think is the positive direction
for rise, up or down? If you said up, pat yourself
on the back. That means down is the negative direction for rise.
A way to remember this is to think about the numbers are on the y-axis.
Going up above the origin are the positive values, and going down below
the origin are the negative values.
What do you think is the positive direction
for run, right or left? If you said right, pat yourself
on the back. That means left is the negative direction for run.
A way to remember this is to think about the numbers are on the x-axis. Going to the right of the origin are the
positive values, and going to the left of the origin are the negative values.
If the slope is positive, then the
rise and the run need to either be BOTH positive or BOTH negative.
In other words, you will be going up and to the right OR down and to
the left. The reason both negative directions work is our slope
is rise over run and if you have a negative over a negative, it simplifies
to be a positive.
If the slope is negative, then the
rise and the run have to be opposites of each other, one has to be positive
and one has to be negative. In other words, you will be going
up and to the left OR down and to the right. If you make them
both negative, then it would simplify to be a positive and you would have
the wrong graph and you don't want to do that.
Also keep in mind, if your slope is a non-zero integer like -5 or 10,
that there is a denominator or run of your slope. What
is the denominator of a non-zero integer? If you said
1, you are correct!!! |
Step 4: Draw
a line through the points found in steps 2 and 3. |
All of the graphs in this tutorial will be straight lines. |
This equation is already in slope/intercept form: |
Lining up the form with the equation we have been given, can you see
what the slope and y-intercept are?
In this form, the slope is m, which
is the number in front of x. In our problem
that would have to be 3.
In this form, the y-intercept is b,
which is the constant. In our problem that would be 1.
How did you do? |
Since the y-intercept is where the line
crosses the y-axis, then x's
value would have to be 0. In step 1 we found our y-intercept
value to be 1.
Putting that together, the ordered pair for the y-intercept
would be (0, 1): |
In step 1 we found our slope to be 3. What would the denominator
of 3 be? If you said 1, you are right on. So we can think of
3 as 3/1. That makes it easier to think of it as rise over run (rise/run).
Since we have a positive slope, the rise and the run need to either
be BOTH positive or BOTH negative. So, we can either rise up 3 and
run right 1 OR go down 3 and left 1.
I chose to rise up 3 and run right 1, starting on the y-intercept:: |
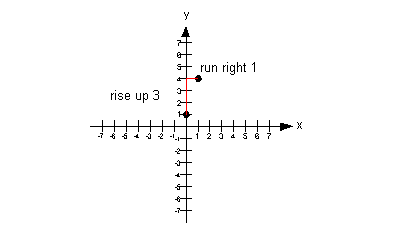
Note that if we would have gone down 3 and left 1 from our y-intercept,
that we would have ended up at (-1, -2) which would have lined up with
the other points. |
Solve for y to get it into the slope/intercept
form: |
|
*Inverse of add. 3x is sub. 3x
*Inverse of mult. 2 is div. 2
*Slope/intercept form
|
Lining up the form with the equation we got, can you see what the slope
and y-intercept are?
In this form, the slope is m, which
is the number in front of x. In our problem
that would have to be -3/2.
In this form, the y-intercept is b,
which is the constant. In our problem that would be 3.
How did you do? |
Since the y-intercept is where the line
crosses the y-axis, then x's
value would have to be 0. In step 1 we found our y-intercept
value to be 3.
Putting that together, the ordered pair for the y-intercept
would be (0, 3): |
In step 1 we found our slope to be -3/2.
Since we have a negative slope the rise and the run have to be opposites
of each other, one has to be positive and one has to be negative.
So, we can either go down 3 and run right 2 OR rise up 3 and run left 2.
I chose to go down 3 and run right 2, starting on the y-intercept: |
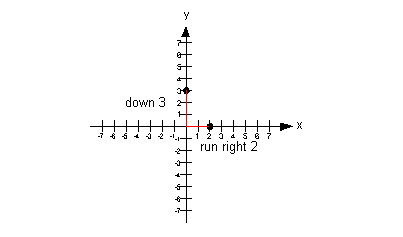
Note that if we rose up 3 and ran left 2 from our y-intercept,
we would have ended up at (-2, 6) which would have lined up with the other
points. |
This equation is already in slope/intercept form: |
Lining up the form with the equation we have been given, can you see
what the slope and y-intercept are?
In this form, the slope is m, which
is the number in front of x. In our problem
that would have to be 5/2.
In this form, the y-intercept is b,
which is the constant. In our problem that would be 0.
How did you do? |
Since the y-intercept is where the line
crosses the y-axis, then x's
value would have to be 0. In step 1 we found our y-intercept
value to be 0.
Putting that together, the ordered pair for the y-intercept
would be (0, 0): |
In step 1 we found our slope to be 5/2.
Since we have a positive slope the rise and the run need to either be
BOTH positive or BOTH negative. So, we can either rise up 5 and run
right 2 OR go down 5 and left 2.
I chose to rise up 5 and run right 2, starting on the y-intercept: |
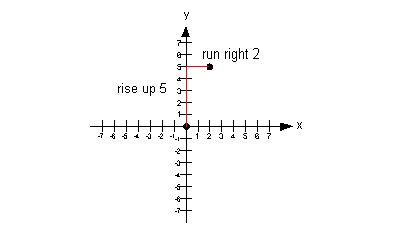
Note that if we would have gone down 5 and left 2 from our y-intercept,
we would have ended up at (-2, -5) which would have lined up with the other
points. |
If you have an equation x = c,
where c is a constant, and you are wanting
to graph it on a two dimensional graph, this would be a vertical line with x-intercept
of (c, 0).
Even though you do not see a y in the equation,
you can still graph it on a two dimensional graph. Remember that
the graph is the set of all solutions for a given equation. If all
the points are solutions, then any ordered pair that has an x value of c would be a solution. As long
as x never changes value, it is
always c, then you have a solution. In
that case, you will end up with a vertical line.
Below is an illustration of a vertical line x = c:
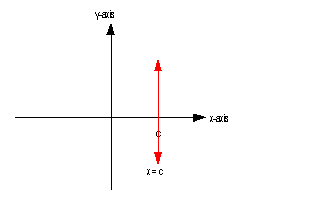
As mentioned above, the slope of a vertical line
is undefined.
Also, note that except for the vertical line x = 0, a vertical
line does not go through the y-axis.
So that means a vertical line has no y-intercept,
unless it is x = 0. |
If you have an equation y = c,
where c is a constant, and you are wanting
to graph it on a two dimensional graph, this would be a horizontal line
with y- intercept of (0, c).
Even though you do not see an x in the equation,
you can still graph it on a two dimensional graph. Remember that
the graph is the set of all solutions for a given equation. If all
the points are solutions, then any ordered pair that has a y value of c would be a solution. As long
as y never changes value, it is always c, then you have a solution.
In that case, you will end up with a horizontal line.
Below is an illustration of a horizontal line y = c:
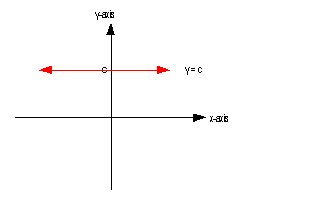
As mentioned above, a horizontal line has a
slope of 0.
A horizontal line's y-intercept is whatever y is set equal to. |
Note how we have an equation that has y set equal to a constant, where there is no x.
Since this fits the form of y = c described above, we can cut to
the chase and draw our horizontal line: |
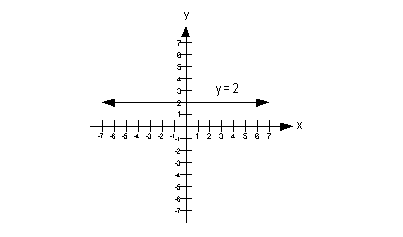
Since we have a horizontal line, what is our slope going to be?
If you said 0, you are so right!!!
What would the y-intercept be? Give
yourself a high five if you said 2. |
Note how we are missing a y and even though
it is not quite in the form x = c,
that we can get it in that form.
Lets first rewrite this in the form x = c and then go from there: |
|
*Written in the form x = c |
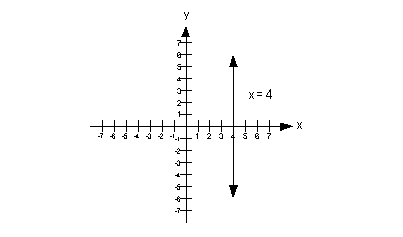
Since we have a vertical line, what is our slope going to be?
If you said undefined, you are so right!!!
What would the y-intercept be? Give
yourself a high five if you said there is no y-intercept. |
Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1d: Give the slope and y-intercept of the
given line and then graph it.
Need Extra Help on these Topics?
Last revised on Feb. 11, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.
|
|
Example
1: Give the slope and y-intercept
of the line 
and
then graph it.
and
then graph it.
and
then graph it.
and
then graph it.
and
then graph it.
