College Algebra
Tutorial 23B: Rational Inequalities
 Learning Objectives Learning Objectives
After completing this tutorial, you should be able to:
- Solve rational inequalities using a sign graph of
factors.
- Solve rational inequalities using the test-point
method.
|
 Introduction Introduction
In this tutorial we will be looking at solving rational
inequalities using two different methods. The methods of solving
rational inequalities are
very similar to solving quadratic inequalities. If you need a
review on solving quadratic inequalities, feel free to go to Tutorial
23A: Quadratic Inequalities. And yes, we will be
dealing with
fractions (yuck!) as we go through the rational inequalities.
I think we are ready to start. |
 Tutorial Tutorial
|
Rational
Inequalities
A rational
inequality is one
that can be written in one of the following standard forms:
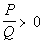
or
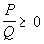
or
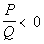
or
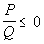
Q does not equal 0.
|
In other words, a rational inequality is in standard
form when the
inequality is set to 0. |
Solving
Rational Inequalities
Using
a Sign Graph of the Factors
|
This
method of solving rational inequalities only works if the numerator and
denominator
factor. If at least one of them doesn't factor then you will need
to use the test-point method shown later on
this page.
This method works in the same fashion as it does with quadratic
inequalities.
If you need a
review on solving quadratic inequalities, feel free to go to Tutorial
23A: Quadratic Inequalities.
Be careful, it is really
tempting to
multiply both sides of the inequality by the denominator like you do
when
solving rational equations. The problem is the expression in the
denominator will have a variable, so we won't know what the denominator
is equal to. Remember that if we multiply both sides of an
inequality
by a positive number, it does not change the inequality. BUT if
we
multiply both sides by a negative, it does change the sign of the
inequality.
Since we don't know what sign we are dealing with we need to go about
it
the way described below. |
Step 1: Write the rational
inequality in standard form. |
It is VERY important that one side of the inequality is
0.
0 is our magic number. It is the only number that
separates the
negatives from the positives. If an expression is greater than 0,
then there is no doubt that its sign is positive. Likewise, if it
is less than 0, its sign is negative. You can not say this about
any other number. Since we are working with inequalities, this
idea
will come in handy. With this technique we will be looking at the
sign of a number to determine if it is a solution or not. |
Step 2: Factor the numerator
and denominator and find the values of x that make these
factors
equal to 0 to find the boundary points. |
The boundary point(s) will mark off where the rational
expression
is equal to 0. This is like the cross over point. 0 is
neither
positive or negative.
As mentioned above, this method of
solving rational inequalities only works if the numerator and
denominator
factor. If at least one of them doesn't factor then you will need
to use the test-point
method shown later on this page. |
Step 3: Use the boundary
point(s) found in step 2 to mark off test intervals on the number line. |
The boundary point(s) on the number will create test
intervals. |
Step 4: Find the sign of every factor in every interval.
|
You can choose ANY value in an interval to plug into
each factor. Whatever the sign of the factor is with that value
gives you the sign you need for that factor in that interval.
Make sure that you find the sign of every factor in every interval.
Since the inequality will be set to 0, we are not
interested in
the actual value that we get when we plug in our test points, but what
SIGN (positive or negative) that we get. |
Step 5: Using the signs found in Step 4, determine the sign of the overall
rational function in each interval.
|
Since the inequality will be set to 0, we are not
interested in
the actual value that we get when we plug in our test points, but what
SIGN (positive or negative) that we get.
When you look at the signs of your factors in each
interval, keep in mind that they represent a product and/or quotient of
the factors
that make up your overall rational function.
You determine the sign
of the overall rational function by using basic multiplication sign
rules:
- The product or quotient of two factors that
have the
opposite signs is negative.
This can be extended if you have more than two factors involved.
|
If the rational expression is
less than or
less than or equal to 0, then we are interested in values that cause
the
rational expression to be negative.
If the rational expression is
greater than
or greater than or equal to 0, then we are interested in values that
cause
our rational expression to be positive. |
Step 6: Write the solution
set and graph. |
This rational inequality is already in standard form. |
Step 2: Factor the numerator
and denominator and find the values of x that make these
factors
equal to 0 to find
the boundary points. |
|
*Set numerator = 0 and solve |
|
*Set denominator = 0 and solve |
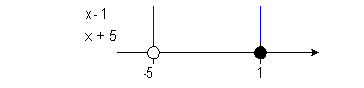
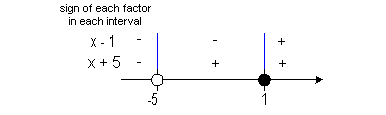
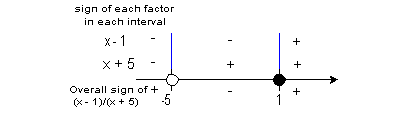
-5 and 1 are boundary points. |
Below is a graph that marks off the boundary points -5
and 1 and shows
the three sections that those points have created on the graph.
Note
that there is a open hole at -5. Since that is the value that
causes
the denominator to be 0, we cannot include where x = -5. Since our inequality includes where it is equal to 0, and 1
causes only the numerator to be 0 there is a closed hole at 1.
Note that the two boundary points create three sections
on the graph: 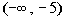 , , 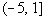 ,
and ,
and 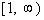 . . |
You can choose ANY point in an interval to represent
that interval.
Remember that we are not interested in the actual value that we get,
but
what SIGN (positive or negative) that we get.
If we chose a number in the first
interval, 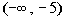 , like -6 (I could have used -10, -25, or -10000 as long as it is in the
interval), it would make both factors negative: , like -6 (I could have used -10, -25, or -10000 as long as it is in the
interval), it would make both factors negative:
-6 - 1 = -7 and -6
+ 5 = -1
If we chose a number in the second
interval, 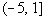 , like 0 (I
could have used -4, -1, or 1/2 as long as it is in the interval), it
would make x - 1
negative and x + 5
positive:
0 - 1 = -1 and 0 + 5 = 5
If we chose a number in the third
interval, 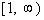 , like 2 (I could have used 10, 25, or
10000 as long as it is in the interval), it would make both factors
positive:
2 - 1 = 1 and 2 + 5
= 7
|
In the first interval, 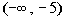 , , we have a
negative divided by a negative, so the sign of the quadratic in that
interval is positive.
In the second interval, 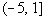 , we have a
positive divided by a negative, so
the sign of the quadratic in that interval is negative.
In the third
interval, 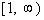 , we
have two positives, so the
sign of the quadratic in that interval is positive.
Keep in mind that our inequality is 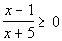 .
Since we are looking for the quadratic expression to be GREATER
THAN OR EQUAL TO 0, that means we need our sign to be POSITIVE
(OR O). .
Since we are looking for the quadratic expression to be GREATER
THAN OR EQUAL TO 0, that means we need our sign to be POSITIVE
(OR O).
|
Interval notation: 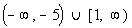
Graph:
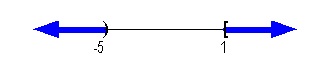 |
*An open interval indicating
all values less
than -5 and a closed interval indicating all values greater then
or equal to 1
*Visual showing all numbers
less than -5 or
greater then or equal to 1
|
Solving
Rational Inequalities
Using
the Test-Point Method
|
The
test-point method for solving rational inequalities works for any
rational function that has a real number solution, whether the
numerator or denominator factors or not.
This method works in the same fashion as it does with quadratic
inequalities.
If you need a
review on solving quadratic inequalities, feel free to go to Tutorial
23A: Quadratic Inequalities.
Be careful, it is really
tempting to
multiply both sides of the inequality by the denominator like you do
when
solving rational equations. The problem is the expression in the
denominator will have a variable, so we won't know what the denominator
is equal to. Remember that if we multiply both sides of an
inequality
by a positive number, it does not change the inequality. BUT if
we
multiply both sides by a negative, it does change the sign of the
inequality.
Since we don't know what sign we are dealing with we need to go about
it
the way described below. |
Step 1: Write the rational
inequality in standard form. |
It is VERY important that one side of the inequality is
0.
0 is our magic number. It is the only number that
separates the
negatives from the positives. If an expression is greater than 0,
then there is no doubt that its sign is positive. Likewise, if it
is less than 0, its sign is negative. You can not say this about
any other number. Since we are working with inequalities, this
idea
will come in handy. With this technique we will be looking at the
sign of a number to determine if it is a solution or not. |
Step 2:
Find the values of x that make the numerator and denominator
equal to 0 to find the boundary points. |
The boundary point(s) will mark off where the rational
expression
is equal to 0. This is like the cross over point. 0 is
neither
positive or negative. |
Step 3: Use the boundary
point(s) found in Step 2 to mark off test intervals on the number line. |
The boundary point(s) on the number will create test
intervals. |
Step 4: Test a point
in each test interval found in Step 3 to see which interval(s) is part
of the solution set. |
You can choose ANY point in an interval to represent
it. You
need to make sure that you test one point from each interval.
Sometimes
more than one interval can be part of the solution set.
Since the inequality will be set to 0, we are not
interested in
the actual value that we get when we plug in our test points, but what
SIGN (positive or negative) that we get.
If the rational expression is
less than or
less than or equal to 0, then we are interested in values that cause
the
rational expression to be negative.
If the rational expression is
greater than
or greater than or equal to 0, then we are interested in values that
cause
our rational expression to be positive. |
Step 5: Write the solution
set and graph. |
|
*Inv. of add. 1 is sub. 1
|
| Step 2: Factor the numerator
and denominator and find the values of x that make these
factors
equal to 0 to find
the boundary points. |
|
*Set numerator = 0 and solve
|
|
*Set denominator = 0 and solve |
-1/4 and 0 are boundary points. |
Below is a graph that marks off the boundary points
-1/4 and 0 and
shows the three sections that those points have created on the
graph.
Note that open holes were used on those two points since our original
inequality
did not include where it is equal to 0 and -1/4 makes the denominator
0.

Note that the two boundary points create three sections
on the graph: 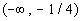 , , 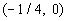 , and , and 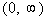 . . |
You can choose ANY point in an interval to represent
that interval.
Remember that we are not interested in the actual value that we get,
but
what SIGN (positive or negative) that we get.
Keep in mind that our original problem is 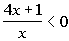 .
Since we are looking for the quadratic expression to be LESS
THAN 0, that means we need our sign to be NEGATIVE. .
Since we are looking for the quadratic expression to be LESS
THAN 0, that means we need our sign to be NEGATIVE.
From the interval 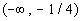 ,
I choose to use -1 to test this interval: ,
I choose to use -1 to test this interval:
(I could have used -10, -25, or -10000 as long as it is in the interval) |
|
*Chose -1 from 1st interval to
plug in for x
|
Since 3 is positive and we are looking for values
that cause our
quadratic expression to be less than 0 (negative), 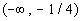 would
not be part of the solution. would
not be part of the solution. |
From the interval 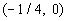 ,
I choose to use -1/5 to test this interval. ,
I choose to use -1/5 to test this interval.
(I could have used -1/6, -1/7, or -1/8 as long as it is in the interval) |
|
*Chose -1/5 from 2nd interval to
plug in for x
|
Since -1 is negative and we are looking for values
that cause our
expression to be less than 0 (negative), 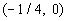 would
be part of the solution. would
be part of the solution. |
From the interval 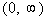 ,
I choose to use 1 to test this interval. ,
I choose to use 1 to test this interval.
(I could have used 10, 25, or 10000 as long as it is in the interval) |
|
*Chose 1 from 3rd interval to
plug in for x
|
Since 5 is positive and we are looking for values
that cause our
quadratic expression to be less than 0 (negative), 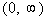 would not be part of the solution. would not be part of the solution. |
Interval notation: 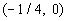
Graph:
 |
*Open interval indicating all
values between
-1/4 and 0
*Visual showing all numbers
between -1/4 and
0 on the number line
|
 Practice Problems Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1b: Solve (using any method), write your
answer in
interval notation
and graph the solution set. Practice
Problems 1a - 1b: Solve (using any method), write your
answer in
interval notation
and graph the solution set.
 Need Extra Help on these Topics? Need Extra Help on these Topics?

Videos at this site were created and produced by Kim Seward and Virginia Williams Trice.
Last revised on Jan. 2, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.
|
|


