

100
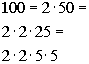
![]()
![]()
![]()
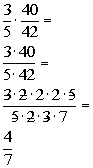
*Div. the common factors of 2 and 5 out of both num. and den.
![]()
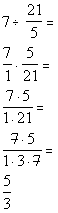
*Write as prod. of num. over prod. of den.
*Div. the common factor of 7 out of both num. and den.
![]()
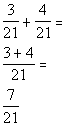
![]()
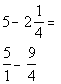
Therefore, the LCD is 4.
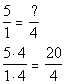
*Multiply num. and den. by 4.
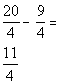
![]()
Therefore, the LCD is 20.
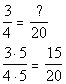
*Multiply num. and den. by 5.
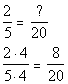
*Multiply num. and den. by 4.
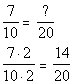
*Multiply num. and den. by 2.
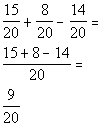
*Write the sum and difference over the common
den.
Last revised on July 24, 2011 by Kim Seward.
All contents copyright (C) 2001 - 2011, WTAMU and Kim Seward.
All rights reserved.